Volume of a Square Box – Definition, Formula, Examples

What Is the Volume of a Square Box?

Volume of a square box is the total space occupied by the square box and it is given by $(side)^3$.

A square box is a box that is cubic in shape. Thus, in a square box, the dimensions of length, width and height measure the same. A square box is a 3D solid object that has:

• 6 square faces
• 8 vertices
• 12 edges

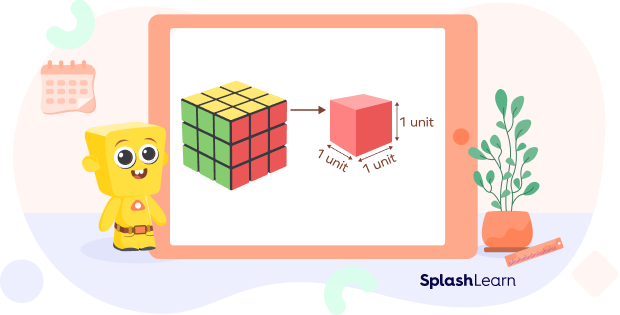
Volume is the space occupied by the 3D shape. It is also defined as the number of unit cubes (a cube with a side of 1 unit) that can be fit into it. Thus, if 27 unit cubes can perfectly fit in the given square box, we can say that its volume is 27 cubic units.

Volume is measured in cubic units, such as cubic feet, $cm^3,\; m^3,\; in^3$, etc. The volume of a square box is calculated by calculating the cube of the side. 

Volume of a Square Box: Definition

The volume of a square box is defined as the cube of length of the side of the square box. Finding the volume of a box is simple once we know the side of the box.

If the side of the square box is “s” units, then its volume is given by

Volume $= s^3$ cubic units

Volume of a Square Box Formula

Based on the discussion above, the formula for the volume of a square box can be formulated through three different methods.

When the Length of the Side Is Given

The formula for the volume of a cube, when the dimensions of the side is given, can be written as:

$Volume\; of\; a\; square\; box = (side)^3$

When the Base Area and Height Is Given

The formula for the volume of a cube when the base area and height is given can be written as:

$Volume\; of\; a\; square\; box = Base\; Area \times Height$

When the Measure of Diagonal Is Given

The formula for the volume of a cube, when the measure of diagonal is given, can be written as:

$Volume\; of\; a\; square\; box\; = \frac{\sqrt{3}\; (diagonal)^3}{9}$

How to Find the Volume of a Square Box

Step 1: If the length of the box is given, use the formula V = s³ to find the volume.

Step 2: If the length of the diagonal is known, use the formula 

$V = \frac{\sqrt{3}\; (diagonal)^3}{9}$

Step 3: If we know the base area and height, use the formula

$V = Base\; Area \times Height$

Facts about Volume of a Square Box

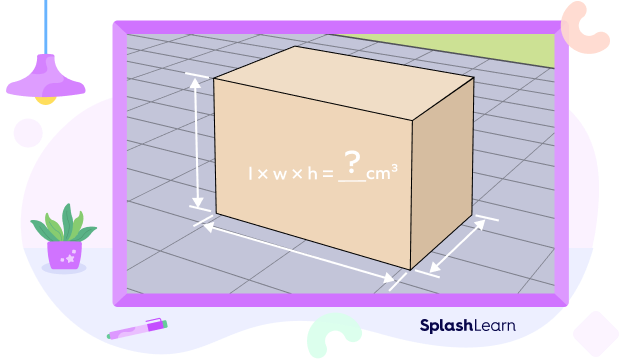
• A rectangular box or a rectangular prism is similar to a square box. However, its three dimensions are not equal. How to calculate volume of a box like this?

The equation for volume of a box shown in the figure is given by: 

Volume of a rectangular prism $=$ lwh

• A square box is the 3D version of a square.

Conclusion

In this article, we learned about the volume of the square box. We saw the different formulas and then the ways to calculate. We solved some practice problems for our better understanding. 

Solved Examples on Volume of a Square Box

1. How to calculate the volume of a box whose dimension is 4 inches?

Solution:

Length of the side, $s = 4$ in

Using the equation for volume of a box square in shape: $V = side^3$

$\Rightarrow$ volume of the square box $= (4\; in)^3$

$\Rightarrow$ volume of the square box $= 64\; inches^3$

Hence, the volume of the square box is 64 cubic inches.

2. The length of the diagonal of a square box is 1 unit. Find the volume of the box.

Solution:

Length of the diagonal $= 1$ unit

Using the formula for the volume of the square box: 

Volume of the square box $= \frac{\sqrt{3} \times diagonal^3}{9}$ 

$\Rightarrow$ Volume of the square box $= \frac{\sqrt{3} \times 1^3}{9} = \frac{\sqrt{3}}{9} = 0.19245$

3. A gift was put in a square box with a length of 12 feet. What is the volume of the box?

Solution:

Length of the side, 

$s = 12$ feet

Using the formula for the volume of the square box: $V = side^3$

$\Rightarrow$ volume of the square box $= (12\; feet)^3$

$\Rightarrow$ volume of the square box $= 1728\; (feet)^3$

Hence, the volume of the square box is 1728 cubic feet.

4. Find the length of the edges of the cube, if its volume is equal to 343 cm³. 

Solution:

Volume of the cube $= 343\; cm^3$.

Let the length of the edges be “s.”

Using the formula for the volume of the square box: $V = side^3$

Substituting the value, we get,

$343 = s^3$

$\Rightarrow s = ^3\sqrt{}343$

$\Rightarrow$ s = 7\; cm$

Hence, the length of the cube is 7 cm.

5. What is the volume of a square box if the base area is 25 square inches.

Solution:

Area of the base $= 25$ square inches

We find the length of the side using the formula:

Area of a square $= side^2$

$25\; in^2 = side^2$

$Side = \sqrt{25}\; in^2$

$Side = 5\; inches$

The volume of a square box when base area and height are given is given by the formula: Base area × Height

So, Volume of the square box $= 25\; in^2 \times 5\; in$

$\Rightarrow$ Volume of the square box $=125\; in^3$

Hence, the volume of the square box is 125 cubic inches.

Practice Problems on Volume of a Square Box

Frequently Asked Questions on Volume of a Square Box