Volume of a Triangular Pyramid: Definition, Example, Facts

What Is The Volume of a Triangular Pyramid?

Let’s imagine you are making homemade chocolate and want to shape it somewhat like Toblerone. You go to the market and buy a triangular pyramid-shaped setting mold. You will need to work out the volume of the triangular pyramid-shaped mold to find the amount of chocolate you need to put into it. 

So, what’s volume? Volume is defined as the space occupied within the boundaries of an object in three-dimensional space. It is also known as the capacity of the object. Volume of a triangular pyramid is the volume of a pyramid with a triangular base.

Triangular Pyramid and Its Parts

A triangular pyramid is a three-dimensional shape with flat triangular faces, straight edges, and sharp corners or vertices. It is made up of three triangular faces and a triangular base. It has four faces, six edges, and four vertices. 

If all four faces of a triangular pyramid are equilateral triangles, then it is called a regular triangular pyramid.

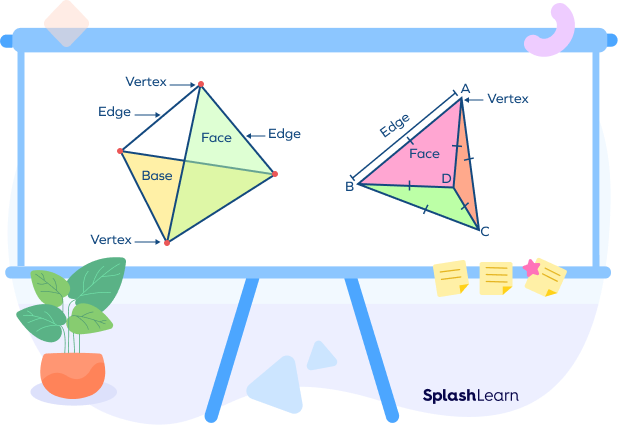
Now that we know what a triangular pyramid is, let’s look at how to find the volume of a triangular pyramid.

The Formula for the Volume of a Triangular Pyramid

The volume of a triangular pyramid is one-third times the product of the area of the base triangle and the height of the pyramid. The triangular pyramid volume formula is

$V = \frac{1}{3} \times B \times h$ cubic units

Here, V is the volume, B is the base area, and h is the height of the pyramid.

Note:

The formula for a regular triangular pyramid volume is:

$V = \frac{a^{3}}{6\sqrt{2}}$ cubic units

Where V is the volume of the regular triangular pyramid, and a is the side of the equilateral triangle.

How to Find the Volume of a Triangular Pyramid

Now that we know the formula, we can find the volume of any triangular pyramid. 

First, we need to know if the given triangular pyramid is a regular triangular pyramid or not. 

• If it is not a regular triangular pyramid then we use the following formula:

$V = \frac{1}{3} \times Area of base \times h$

• Find the area of the base of the triangle. 

The area of a triangle is half of the product of the base of the triangle and the height of the triangle. 

$A = \frac{1}{2} \times b \times h$    

Here, A is the area of a triangle, b is the base of the triangle, and h is the height of the triangle. 

If the base triangle is an equilateral triangle with the side “a’’ then we can find its area with the following formula:
$A = \frac{\sqrt{3}}{4} \times a^{2}$
Here, A is the area of a triangle, and a is the side of the equilateral triangle.

• Now, plug in the values of the area of the base and height in the formula mentioned earlier and simplify. The result is the volume of the triangular pyramid. 

• If it is a regular triangular pyramid then use the following formula:

$V = \frac{a^{3}}{6\sqrt{2}}$

Remember to write the unit! Volume is measured in cubic units.

Facts about the Volume of a Triangular Pyramid

• A regular triangular pyramid is also called a tetrahedron. 
• The volume of a triangular pyramid is represented in cubic units or another format of writing cubic unit as this is commonly used (unit)³, such as cubic centimeters, cubic inch, cubic foot, cubic meter, etc.
• A Rubik’s triangle is an example of a triangular pyramid.
  
  Image alt text: Triangular pyramid: real-life example

Conclusion

The volume of a triangular pyramid is an important concept for learners. This can be better understood with practical examples. Using SplashLearn, students can practice each example with online interactive worksheets. This game-based learning app makes learning fun and keeps your child engaged.

Solved Examples for the Volume of a Triangular Pyramid

1. What is the volume of a triangular pyramid if its base area is 19 sq. inches and its height is 1.5 inches?

Solution:

It is given that base area $B = 19$ sq. inches and height of the pyramid $= 1.5$ inches. 

We know Volume $= \frac{1}{3} \times B \times h$

Substituting the values we get,

$Volume = \frac{1}{3} \times 19 \times 1.5$

$Volume = 19 \times 0.5$

$Volume = 9.5\; cubic\; inches$

2. Find the height of a triangular pyramid with a base area of 175 sq. units and a volume of 1050 cubic units.

Solution:

It is given that B $= 175$ and V $= 1050$.

Volume of a triangular pyramid $= \frac{1}{3} \times B \times h$

$1050 = \frac{1}{3} \times 175 \times h$

Rearranging the values we get,

$h = \frac{3 \times 1050}{175}$

$h = 18\; units$

So, the height of the pyramid is 18 units.

3. What is the volume of a regular triangular pyramid with a side of length 92 units? 

Solution: 

It is given that the side of a regular triangular pyramid i.e. $a = 9\sqrt{2}$ units.

We know that the volume of a regular triangular pyramid is 

$V = \frac{a^{3}}{6\sqrt{2}}$

Substituting “a” as $9\sqrt{2}$ we get

$V = \frac{(9\sqrt{2})^{3}}{6\sqrt{2}}$

$V = \frac{9\sqrt{2} \times 9\sqrt{2} \times 9\sqrt{2}}{6\sqrt{2}} = 243$ cubic units

So, the volume of the regular triangular pyramid is 243 cubic units.

4. Find the height of a regular triangular pyramid having a volume $18\sqrt{2}$ cubic units. 

Solution: 

It is given that the volume of a regular triangular pyramid, i.e., $V = 18\sqrt{2}$ cubic units.

We know that the volume of a regular triangular pyramid is: 

$V = \frac{a^{3}}{6\sqrt{2}}$

Substituting “V” as $18\sqrt{2}$ we get

$18\sqrt{2} = \frac{(a)^{3}}{6\sqrt{2}}$

$a^{3} = 18\sqrt{2} \times 6\sqrt{2}$

$a^{3} = 216$

Taking a cube root on both sides, we get

$a = 6$ units

So, the height of the regular triangular pyramid is 6 units.

5. Find the percentage change in the height of a triangular pyramid if its volume was increased to 75 cubic ft from 50 cubic ft, keeping the area of the base the same. 

Solution:  

Let the volume before increasing the height be V1 and the volume after increasing the height be $V_{2}$ .

It is given that $V_{1} = 50$ and $V_{2} = 75$ .

We know, Volume$= \frac{1}{3} \times B \times h$

So, $V_{1} = \frac{1}{3} \times B \times h_{1} = 50$ and $V_{2} = \frac{1}{3} \times B \times h_{2} = 75$ 

To find the percentage change in h, we need to find $\frac{h_{2}}{h_{1}} \times 100$. For this, we need to divide $V_{2}$ by $V_{1}$.

$\frac{V_{2}}{V_{1}} = \frac{^{\frac{1}{3} \times B \times h_{2}}}{^{\frac{1}{3} \times B \times h_{1}}} = \frac{75}{50}$ 

$\frac{h_{2}}{h_{1}} = \frac{3}{2}$

Multiplying both sides by 100.

$\frac{h_{2}}{h_{1}} \times 100 = \frac{3}{2} \times 100$

$\frac{h2}{h1} \times 100 = 1.5 \times 100 = 150\%$

Therefore, the percentage increase in height is $150\%$.

Practice Problems on the Volume of a Triangular Pyramid

Frequently Asked Questions on the Volume of a Triangular Pyramid