What is Y Intercept? Definition, Formula, Equation, Examples

What Is Y-Intercept?

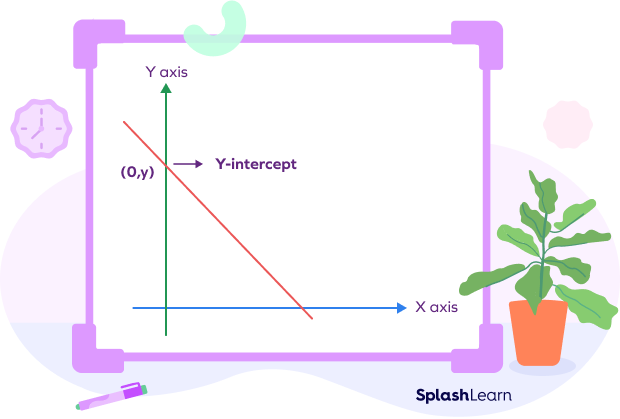
The y-intercept of a graph is the point where the graph crosses the y-axis. 

Since the y-intercept is a point on the y-axis, its x-coordinate is always 0. Thus, the coordinates of the y-intercept are of the form (0, y).

Take a look at the y-intercept of a line on a graph shown below.

Note: 

If the graph is the graph of a function, then it has at most one y-intercept. According to the vertical line test, a graph represents a function if and only if it crosses every vertical line only once. Considering the y-axis as one such vertical line, the graph of a function cannot have more than one y-intercept.

Y-Intercept Definition

The point at which the graph function crosses the y-axis is called the y-intercept. 

Y-Intercept Formula

The y intercept is of the form of (0, y). So, to find the y-intercept of a function, substitute x = 0 and solve for y. 

Y-intercept example:

Let the equation of a line be y=10x+4.

Substitute x = 0.

y = 10(0) + 4

y = 0 + 4

y = 4

Thus, the y-intercept of the line is (0, 4).

Y-Intercept of a Straight Line

The y-intercept of a straight line is the point where the line intersects the y-axis. A line has only one y-intercept.

Finding the y-Intercept of a Line using General Form

The general form of the equation of the straight line is ax+by+c=0

To find y-intercept, substitute x = 0 and solve for y.

a(0)+ by + c =0

0+ by + c =0

by = -c

$y = \;-\;\frac{c}{b}$

The y-intercept of a line ax + by + c = 0  is (0, $\frac{-c}{b}$) or simply  $\frac{-c}{b}$.

Finding the y-Intercept of a Line using Slope-Intercept Form

The slope-intercept form of the equation of the line is y = mx + b, where m is the slope and b is the y-intercept of the line.

To find y-intercept, substitute x = 0 and solve for y.

y = mx + b

y = m(0) + b

y = b

The y-intercept of the equation of a line in  slope-intercept form is  (0, b) or b.

Finding the y-Intercept of a Line using Point-Slope Form

The point-slope form of the equation of the line is given by (y – y₁) = m(x – x₁), where m is the slope of the line and (x₁, y₁) is a point on the line.

To find y-intercept, substitute x = 0 and solve for y.

y- y₁ = m(0 – x₁)

y – y₁ = – mx₁

y = – mx₁ – y₁

y = y₁ – mx₁

The y-intercept of the a line in point-slope (y – y₁) = m(x – x₁) form is  (0,  y₁ – mx₁) or(y₁ – mx₁).

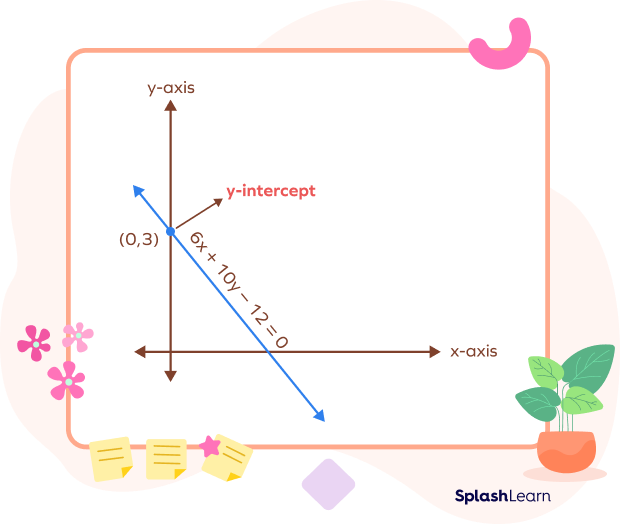
Y-Intercept on a Graph

The point where the graph crosses the y-axis is the y-intercept. 

Example: The line intersects the y-axis at (0, 3). Thus, the y-intercept is (0, 3) or 3.

Y-Intercept of a Quadratic Function (Parabola)

The quadratic function has the standard form y = ax² + bx + c. The y-intercept is always equal to the value of c. 

To find the y-intercept, we just have to substitute x = 0 in the equation and solve for y. Thus, the corresponding y-intercept will be y or (0, y).

Example: y = x² – 2x – 3

Substitute x = 0 and solve for y.

y=0 – 2(0) – 3

y = – 3

Thus, the y-intercept is -3 or (0, -3).

Facts on Y-Intercept

Conclusion

In this article, we have learned about the y-intercept, definition, formula, and its different form with examples. Now, let us solve a few examples and practice problems on y-intercept.

Solved Examples on Y-Intercept

Example 1: Identify the y-intercept of the line y = 2x – 4

Solution:

To find y-intercept, substitute x = 0 and solve for y.

y = 2(0) – 12

y = -12

Thus, the y-intercept of the line y = 2x – 4 is (0,- 12).

Example 2: Find the y-intercept of the following quadratic function: y = x² – 6x + 4

Solution: 

To find y-intercept, substitute x = 0 and solve for y.

y = 0² – 6(0) + 4

y = 4

Thus, the y-intercept of the equation  y = x² – 6x + 4 is (0, 4).

Example 3: If (0,-3) is the y-intercept of the function y = 3x² + ax + b, then find the value of b.

Solution: 

Equation: y = 3x² + ax + b

Y-intercept = (0,–3)

b = ?

Using the y-intercept formula, substitute x = 0 in the given equation,

y = 3x² + ax + b

y = 3(0)² + a(0) + b

y = b

Thus, b = –3

Practice Problems on Y-Intercept

Frequently Asked Questions about Y-intercept