What Is a Zero Slope in Math?
Slope is a measurement of the rate of change. Have you ever wondered what the term “zero slope” means? In this case, you have come to the right place. In this article, we define zero slope and discuss what it means in geometry. To help you understand how this idea works, we’ll also give you some examples of zero-slope equations and straight lines.
Imagine driving your bicycle on a straight horizontal line and driving your bicycle uphill? Of course, driving a bicycle on a horizontal line will be easy since the slope of a horizontal line is zero.
Zero Slope Definition
A line having zero slope is a horizontal line parallel to x-axis. Thus, a line with a zero slope is perpendicular to the y-axis of the coordinate plane.
The line with zero slope forms an angle of $0^{\circ}$ or $180^{\circ}$ with the positive x-axis. The value of the y coordinates is constant on a line with a slope of zero. Only the x-values change.
Example: The red line is parallel to the x-axis and has zero slope.
Recommended Games
What Does Zero Slope Mean in Math?
A line with zero slope is a horizontal line parallel to x-axis.
On a graph, a slope of a line is calculated by the formula “rise over run” or $\frac{Rise}{Run}$.
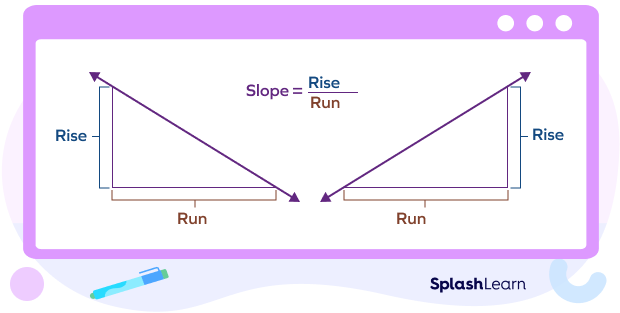
Thus, if a line passes through points $(x_1,\;y_1)$ and $(x_2,\;y_2)$, the slope is given by
slope $= m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} = \frac{\Delta y}{\Delta x}$
For a horizontal line, there is no “rise.” If you pick any two points on a horizontal line, their y-coordinate will be the same. So, we get $\Delta y = 0$.
Thus, slope of a horizontal line $= 0$
Recommended Worksheets
Types of a Slope of a Line
There are four main types of slope plots:
Positive Slope
A line positive slope can be imagined as running uphill. The y-value increases as the x-value increases.
Negative Slope
You can compare it to running downhill. Here, the value of y decreases as the value of x increases.
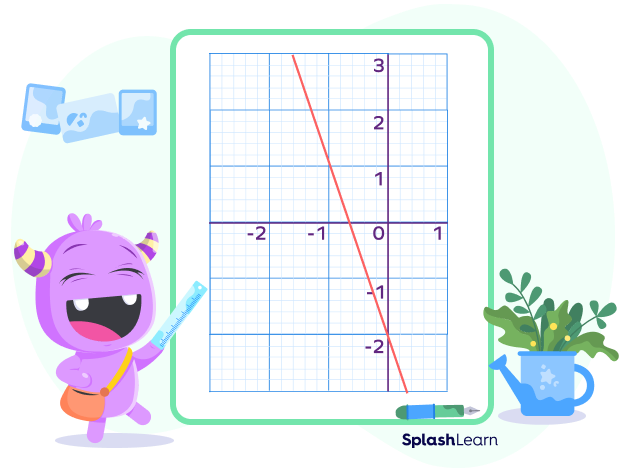
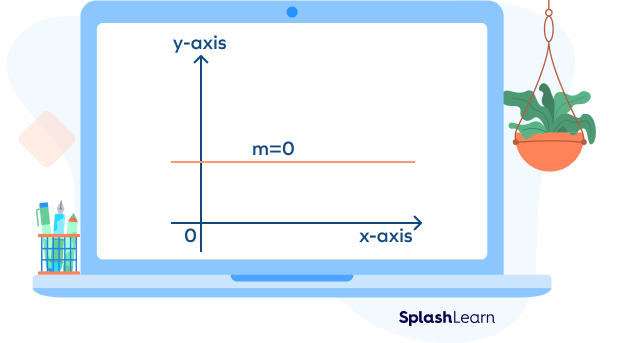
Zero Slope
The slope is zero when a line doesn’t have any vertical rise. This will be a straight horizontal line. It will remain the same from left to right. See the figure below.
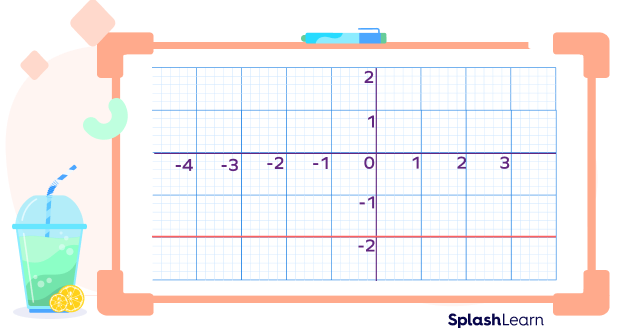
Undefined Slope
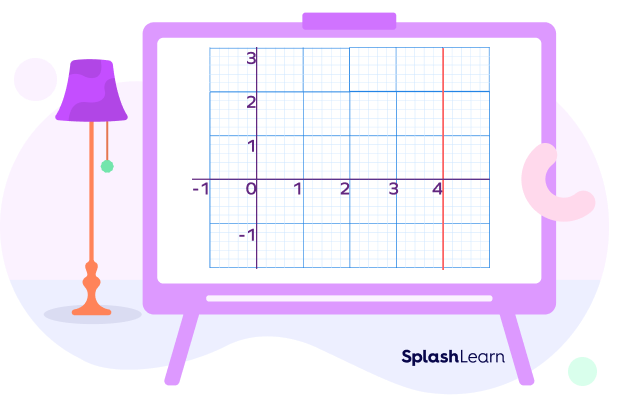
The undefined slope refers to the slope of a vertical line. The x coordinate remains the same. So, in the “rise over run” formula the denominator becomes zero. The equation of a line having undefined slope is of the form $x = b$, where b is a constant.
Zero Slope Form
The formula for the slope point form of a straight line is $y = mx + b$, where
y: the y coordinate of a point on the line
m: slope
x: the x-coordinate of a point on the line
b: y-intercept
Now, we can plug in a slope of “0” for m and see how it changes the formula:
$y = 0x + b$
$y = 0 + b$
0 can be removed from the formula, we get:
$y = b$
This is the zero slope form.
Zero Slope Line
What does a zero slope line look like? It is a line parallel to the x-axis. It’s a horizontal line.
Some of the examples of equations for the zero slope line are:
$y = 5$
$y = 8.7$
$y = -\;19$
b can be equal to any number, positive or negative, integer or rational, or any other real number.
Zero Slope Equation
The zero slope equation or the equation of a line having zero slope can be written as
$y = b$. It is also written as $y = c$.
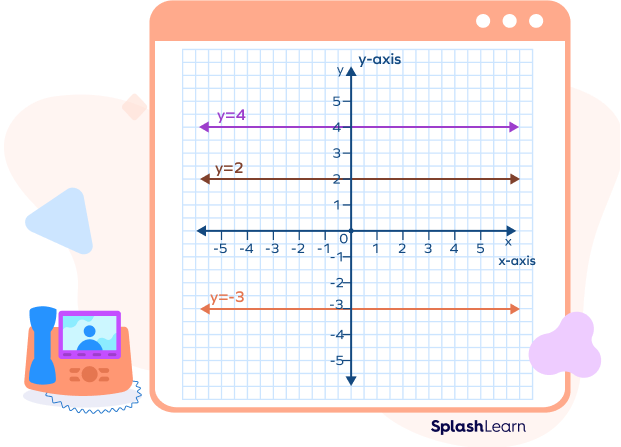
Zero Slope Graph
The graph of a line with zero slope gives a line parallel to the x-axis. The following graph shows examples of lines having zero slope.
Zero Slope Vs Undefined Slope
The slope of the line can be positive, negative, zero, or undefined.
| Zero slope | Undefined slope |
| The slope of a horizontal line is zero because it does not rise vertically $(y_1 \;−\; y_2 = 0)$. | The slope of a vertical line is undefined because it does not run horizontally $(x_1 \;−\; x_2 = 0)$. |
How to Calculate Zero Slope
The zero slopes of a line can be calculated using three simple methods. The zero slopes of a line can be calculated from the points on the line, the angle the line makes with the positive x-axis or the derivative of the line/curve equation. For two points $(x_1,\;y_1)$and $(x_2,\;y_2)$ on a straight line, the slope can be calculated using the formula $m = \frac{(y_2\;-\;y_1)}{(x_2\;-\;x_1)}$
Also, if is the angle the line makes with the positive x-axis in the counterclockwise direction, then the slope of the line can be calculated using the tangent of that angle $\theta$. The zero-slope lines make an angle of $0^{\circ}$ or $180^{\circ}$. We calculate the slope using the formula $m = tan\; 0^{\circ} = tan\; 180^{\circ} = 0$.
For a given equation for a curve f(x), the slope of the curve is the slope of the tangent to a point on the curve, computed by differentiating the function. $m = f'(x) = dy/dx$.
Why Do Horizontal Lines Have Zero Slope?
The slope of a line is defined as
$Slope = \frac{(Rise)}{(Run)}$
The rise of a horizontal line is zero since the y-coordinate is constant.
Thus, the slope is zero.
What Kinds of Lines Have Zero Slope?
The x-axis or the horizontal axis has 0 slope.
Also, as mentioned above, all horizontal lines or the lines parallel to the x-axis have 0 slope.
Fun Facts!
- A line with zero slopes is perfectly flat in the horizontal direction.
- A horizontal line has a slope of zero since it does not rise vertically.
- We cannot divide by zero, we say the slope of a vertical line is infinite.
Conclusion
In this article, we learned about lines with zero slope. We also discussed the graph, equation, and facts. Let’s solve a few examples and practice problems to understand the concept better.
Solved Examples On Zero Slope
1. Consider a line with a slope of 0. Find a point on the same line that is 6 units away from the point (5, 8).
Solution:
Given that the slope of the given line is zero, the value of “y” will not change. Any additional point on the line will therefore have the form $(x,\; 8)$.
As the direction is not specified, the point that is six units away from $(5,8)$ might either be $(5 + 6,\; 8)$ or $(5\;-\;6,\; 8)$.
Therefore, the point can be either$(11,\; 8)$ or $(\;-\;1,\;8)$ for the specified line.
2. Find the slope of the given line.
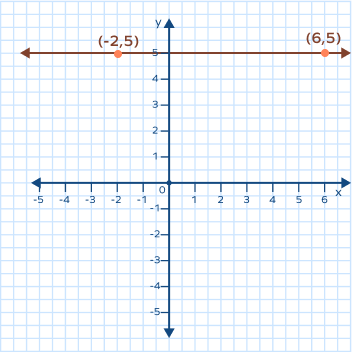
Solution:
The line on the graph is horizontal. Its slope is zero.
As we can see, the two points on line are $(\;-\;2,\; 5)$ and $(6,\; 5)$. We’ll use those two points to determine the slope.
$Slope = m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$ [Slope formula]
$\Rightarrow m = \frac{5 \;–\; 5}{6 \;−\; (\;−\;2)}$
$\Rightarrow m = \frac{0}{8}$
$\Rightarrow m = 0$
3. How do we find the slope of the x-axis?
Solution:
$y = 0$ is the equation of the x-axis.
The equation can be rewritten as $y = 0.x + 0$.
Compare it with the general equation $y = mx + c$
We get, $m = slope = 0$
The slope of the x-axis is 0
4. Determine the slope of the given line.
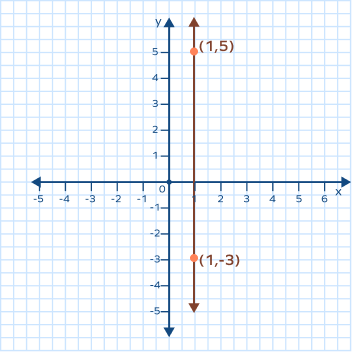
Solution:
The line on the graph is vertical. Its slope is therefore undefined.
Let’s calculate the slope using the slope formula to verify our conclusion.
The graph’s two points are (1, 5) and (14), respectively (1, -3). So,
$Slope = m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$ [Slope formula]
$\Rightarrow m = \frac{(\;−\;3)\;−\;5}{1\;–\;1}$
$\Rightarrow m = \frac{−8}{0}$
$m = undefined$
Therefore, the slope of the graph is undefined.
5. Determine the point on the horizontal line that should be 5 units away from this point (2,6).
Solution:
Given a horizontal line, we can infer that it has a slope of zero, meaning that the value of “y” will remain constant. Therefore any additional point on the line will be of the form $(x,\;6)$.
Since the direction has not been specified, the point might either be $(2 + 5,\; 6)$ or $(2\;-\;5,\; 6)$.
So, the point can either be $(7,\;6)$ or $(\;-\;3,\;6)$ for the given line.
Practice Problems On Zero Slope
Zero Slope - Definition, Types, Graph, Equation, Examples
Identify the lines with zero slope.
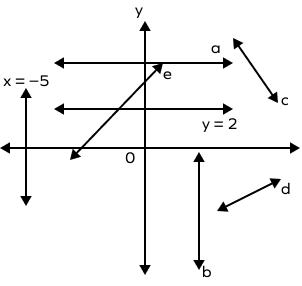
Line a and line $y = 2$ are horizontal lines on the graph. As a result, the slope of line a and line $y = 2$ is zero.
Line b and line $x = \;-\;5$ form a vertical line on the graph. As a result, the slope of “lines b and $x = \;-\;5$” is undefined.
What would be the slope of the line that is parallel to the y-axis?
Undefined slope refers to the slope of vertical lines.
Find the distance of a line from x-axis if it has zero slope and is passing through the point $(4,\; 5)$.
The line with zero slopes is parallel to the x-axis. Thus, the distance of the line from x-axis $=$ y-coordinate $=$ 5 units
A line which makes an angle of 90 degrees with the positive direction of the x-axis has _____________.
A line that makes an angle of 90 degrees with the positive direction of the x-axis has an undefined slope.
The line $y = 6$ has _____ slope.
$y = 6$ is a horizontal line, parallel to the x-axis. Thus, it has zero slope.
Frequently Asked Questions On Zero Slope
How can we identify a line with a zero slope?
A line with zero slope is a perfectly horizontal line parallel to the x-axis..
Do lines that are parallel have the same slope?
For two or more parallel lines, the rise to run ratio is equivalent. Thus, the slope of parallel lines is the same.
What will be the slope of the y-axis?
The slope of y-axis is not defined.
What happens to the line’s behavior when the slope is zero?
Zero slope indicates that the line is horizontal; it does not rise or fall as we move from left to right.
Are the slopes of two perpendicular lines equal?
No, the slope of two perpendicular lines are not the same. However, their product is -1.




























