Adding Integers: Definition, Rules for Addition, Examples

What Is Adding Integers?

Finding the sum of two or more integers is known as adding integers. These integers may have the same or different signs. 

We can define integers as numbers that can be written without a fractional component. Fractions can be positive, negative, or zero. The set of integers includes positive integers, negative integers, and 0. It is given by $Z = \left\{…,-3,-2,\;-\;1, 0, 1, 2, 3, …\right\}$

Three Main Cases to Consider When Adding Integers

When adding two integers, we come across the following situations:

• Addition of two positive integers $(a + b)$
• Addition of two negative integers  $\left[(\;-a) + (\;-b)\right]$
• Addition of a negative integer and a positive integer $\left[a +(\;-b)\right]$

How to Add integers

We can add integers with the help of the rules for addition of integers with different signs, which have been discussed below.

Positive integer $+$ Positive integer $=$ Positive integer

Negative integer $+$ Negative integer $=$ Negative integer

When two integers of the different signs are added, we perform subtraction and add the sign of the number with the largest absolute value.

Let’s learn these rules in detail with examples.

What Are the Rules for Adding Integers?

When adding two or more integers, certain rules must be followed. 

• The sum of an integer and its additive inverse is equal to 0. 

Example: $2 + (\;–2) = 0$

• The addition of two positive integers will be positive. 

Example: $3 + 5 = 8$

• The addition of two negative integers will be negative. 

Example: $–3 + (\;– 5) =  –8$

• When two integers of the different signs are added, only subtraction will be performed and the sign of the result will be the same as the number with the largest absolute value. 

Examples: $–3 + 5 =  2$

      $3 + (\;– 5) =  –2$

• The result of adding integers with 0 is the same number. 

Example: $2 + 0 = 2$.

Integer Addition Rules Chart

The rules for addition with examples of adding integers are summarized in the table below:

Type of Numbers	Operation	Result	Example
Positive + Positive         $(+) + (+)$	Add	Positive $(+)$	$8 + 5 = 13$
Negative + Negative          $(–) $+ (–)	Add	Negative $(-)$	$(–8) + (–5) = –13$
Positive + Negative $(+) + (–)$	Subtract	Sign of the number with the largest absolute value	$(8) + (–5)= 3$
Negative + Positive $(–) + (+)$	Subtract	Sign of the number with the largest absolute value	$(–8) + (5)= –3$

Adding Integers with the Same Sign

The addition of two positive integers will have a positive sign. 

Example: $5 + 8 = 13$

The addition of two negative integers will have a negative sign. Here, we find the sum of the absolute values and add the negative sign to the sum.

Example: $–5 + (\;– 8) =  –13,$

Adding Integers with Different Signs

When two integers of the different signs are added, only subtraction will be performed and the sign of the result will be the same as the number with the largest absolute value. 

Example: $– 4 + 8 = 4$

$5 + (\;– 7) =  –2$

In other words, to add integers with different signs, subtract the absolute values of two integers with different signs, and then attach the sign of the number with the greater absolute value.

Adding Integers on a Number Line

Zero is placed at the center of the number line. All positive integers lie on the right side of zero, and all negative integers lie on the left side of zero.

To add integers on a number line, apply the following rules:

• Draw a number line, and look for the first addend, i.e., starting point. The starting point for moving along the number line is any of the given integers.
• To add a positive integer, move to the right side (or positive side) of the number line.
• To add a negative integer, move to the left side (or negative side) of the number line.
• The result of the addition is where you land on the number line.

Example 1: $(–3) + 4$ on the number line.

Draw a number line, and look for the starting point. Here, $–3$ is the starting point.

Now, to add a positive integer 4, move 4 units to the right side (or positive side).

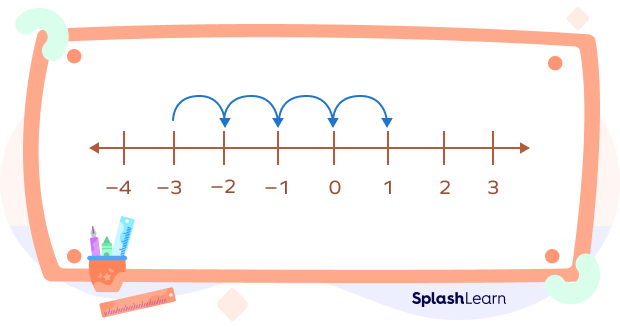
We landed on the number 1. 

Thus, $–3 + 4 = 1$.

Example 2: $2 + (\;–5)$ on the number line.

Draw a number line, and look for the starting point. Here, 2 is the starting point.

Now, to add a negative integer $–5$, move 5 units to the left side (or negative side).

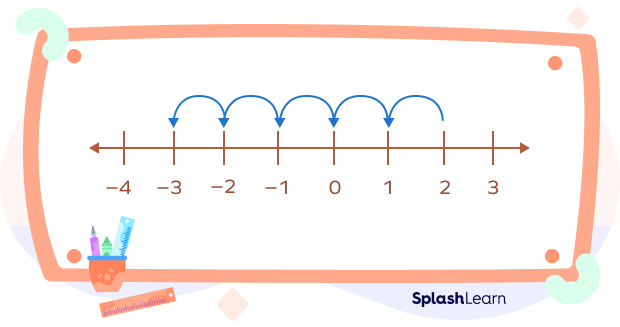
We landed on the number –3.

Thus, $2 + (\;–5) = –3$.

Example 3: $5 + 4$ on the number line

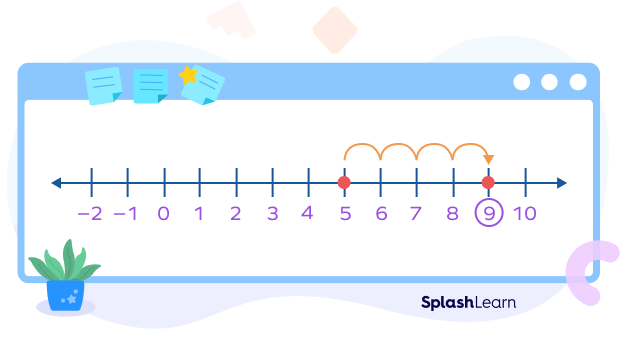
Properties of Addition of Integers

When adding two or more integers, the following properties can be used to simplify expressions and speed up the calculations.

Closure Property

The sum of two integers is always an integer.

For integers a and b, the sum $a + b$ is also an integer.

Commutative Property

The sum of two integers is not affected by the order of the integers.

$a + b = b + a$

Associative Property

The sum of three integers is not affected, no matter how we group three or more integers.

$(a + b) + c = a + (b + c)$

Additive Identity

The additive identity for integers is 0. Adding 0 to any integer results in the same integer.

$a + 0 = a$

Additive Inverse

The sum of an integer and its additive inverse is 0. For any integer a, the additive inverse is -a.

Facts about Adding Integers

• The sum does alter when the order of the numbers added is changed.
• Adding zero to a number gives the number itself.
• When we add 1 to a number, we get the next number.

Conclusion

In this article, we have discussed different rules of adding integers, adding integers on number lines, facts based on integer addition, solved examples, and some important FAQs.

Solved Examples on Adding Integers

1. Using the rules for adding integers, find the sum $12 + 13$.

Solution:

The sum of two positive integers is always positive. 

Hence, $12 + 13 = 25$

2. Using the rules for adding integers, add the integers $7,\; −9$, and 12.

Solution:

Given integers are $7, \;−9,$ and 12. 

We have to find $7 + (\;−9) + 12$.

In such a case, first, add both the positive integers 7 and 12. 

$7 + 12 = 19$. 

So, the expression becomes $19 + (\;−9)$.

Subtract 9 from 19 and give the positive sign.

$19 + (\;−9) = 10$. 

3. Find which number should be added to 14 to get $−5$ as the result.

Solution:

“x” should be added to 14 to get $−5$ as the result.

Therefore, 

$14 + x = −5$

$14 + x = -5$

$x = -5 \;-\;14$

$x = -5 + (\;-14)$

$x = -19$

Hence, $−19$ should be added to 14 to get $−5$ as the result.

4. Using the number line, find $4 + (\;-7)$.

To find $4 + (\;-7)$, we have to move 7 steps to the left from 4. That will give us the answer $−3$.

5. Joe spent $\$35$ on groceries on Monday. He spent $\$13$ more than that on Tuesday. How much did he spend on groceries in total?

Solution:

Money spent for groceries on Tuesday $= \$35 + \$13 = \$48$

Now, money spent for groceries on both days $= \$35 + \$48 = \$83$

Practice Problems on Adding Integers

Frequently Asked Questions on Adding Integers