What Are Adjacent Angles?
Two angles that share a common side and a common vertex (but do not overlap) are called adjacent angles. One angle should not be in the interior of the other angle.
An angle is formed when two rays meet at a common endpoint. The common point of contact is called the vertex of an angle.
Adjacent Meaning in Math:
When two things are placed right next to each other, we say they are “adjacent.” In mathematics, when we use terms such as adjacent angles, adjacent sides, etc,
it means “adjoining” or “side-by-side.” Simply put, adjacent angles are angles lying next to each other.
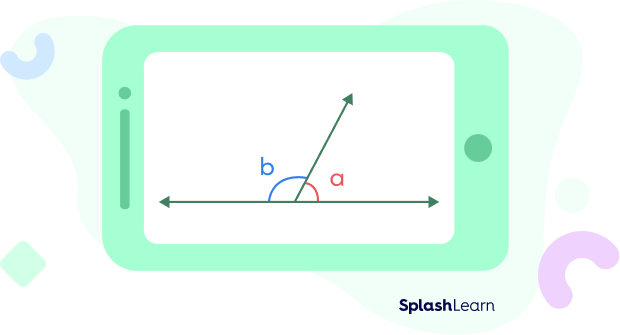
Adjacent Angles example:
Angles $\angle a$ and $\angle b$ form a pair of adjacent angles.
Recommended Games
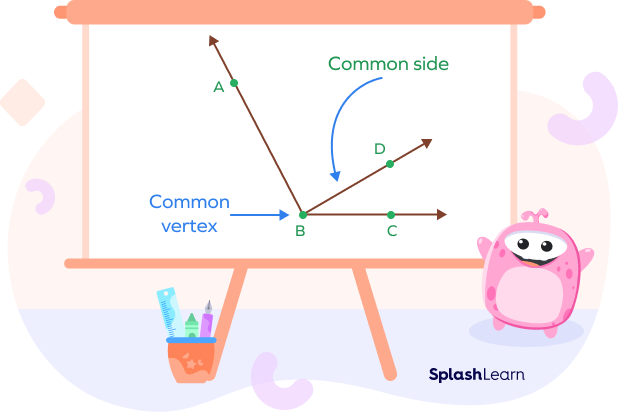
Adjacent Angles Definition
Adjacent angles are two angles that share a common side and a common vertex, and do not overlap.
In the given diagram, the angles $\angle ABD$ and $\angle CBD$ are adjacent angles. They share the common arm or common side BD and a common vertex B.
Recommended Worksheets
Properties of Adjacent Angles
- Adjacent angles share a common side (arm).
- Adjacent angles share a common vertex.
- Adjacent angles do not overlap.
- Adjacent angles have a non-common arm on both sides of the common arm.
- Adjacent angles do not have a common interior point.
How to Identify Adjacent Angles
The presence of a common side and a common vertex is the simplest way to identify an adjacent angle. If two angles share one common side and both can be derived from the same vertex point, then they are adjacent angles.
It is important to remember that adjacent angles must have BOTH a common side and a common vertex. Let’s see some examples and non-examples.
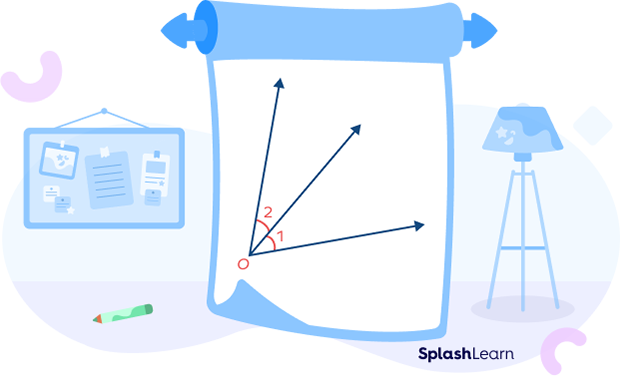
Example 1: Angles 1 and 2 are adjacent angles.
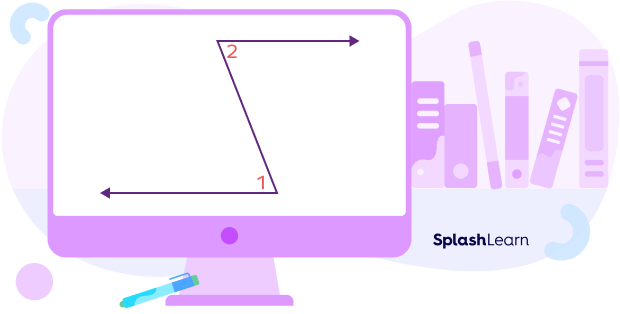
Example 2: In the given diagram, the angles 1 and 2 are not adjacent. Angles 1 and 2 are angles that share one side but not a common vertex.
Examples and Non-Examples of Adjacent Angles
Adjacent angles share a common vertex and a side.
Angles are not adjacent when they only share a common vertex but not a side.
Angles are not adjacent when they only share a common side, but not a vertex.
Angles are not adjacent when angles overlap.
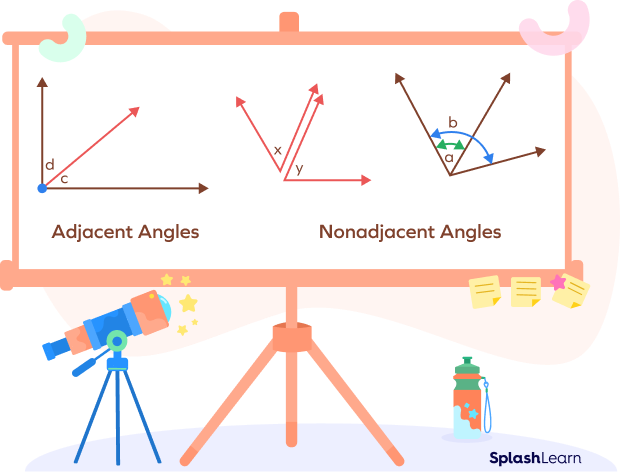
In the diagram below,
- $\angle c$ and $\angle d$ are adjacent angles.
- $\angle x$ and $\angle y$ are not adjacent because they do not share a common side and a common vertex.
- $\angle a$ and $\angle b$ are not adjacent since $\angle a$ is in the interior of the $\angle b$. Here, $\angle b$ overlaps $\angle a$.
What Is the Difference between Vertical and Adjacent Angles?
When two lines intersect, the opposite angles formed are called vertical angles. Vertical angles are also called vertically opposite angles.
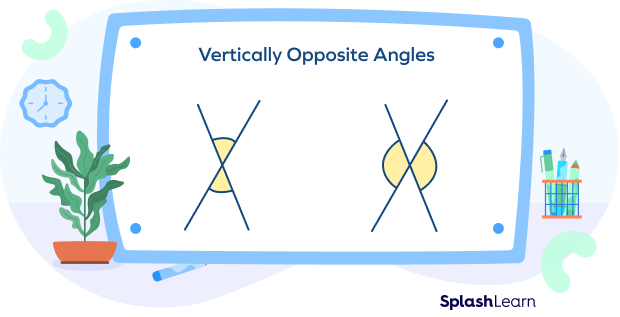
Let’s understand the difference between adjacent angles and vertical angles.
| Adjacent Angles | Vertical Angles |
|---|---|
| Adjacent angles share a common vertex and a common side. | Vertical angles only share a common vertex. |
| These angles are adjoining. They lie exactly next to each other. | These angles lie exactly opposite each other. |
| Adjacent angles need not be congruent. | Vertical angles are always congruent. |
Facts about Adjacent Angles
- Angles forming a linear pair are always adjacent.
- If the sum of two adjacent angles is 90 degrees, they are complementary to each other. However, angles need not be adjacent to be complimentary.
- If the sum of two adjacent angles is 180 degrees, they are supplementary to each other. However, angles need not be adjacent to be supplementary.
| Angles forming a linear pair are always adjacent.If the sum of two adjacent angles is 90 degrees, they are complementary to each other. However, angles need not be adjacent to be complimentary.If the sum of two adjacent angles is 180 degrees, they are supplementary to each other. However, angles need not be adjacent to be supplementary. |
Conclusion
In this article, we learned about adjacent angles. We came to know about the properties, differences from other types of angles. We also solved some practice problems to understand the concept better.
Solved Examples on Adjacent Angles
1. Look at the hands of the given clock. Do they form a pair of adjacent angles?

Solution:
The hands of a clock form a pair of adjacent angles. The second hand represents the common arm. One angle is formed by a minute hand and a second hand. The other angle is formed by the second hand and the hour hand. We can draw it as shown below.

2. Are the angles marked A and B in the following figures adjacent? Support your answers with reasons.
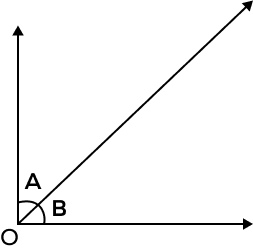
Solution:
$\angle A$ and $\angle B$ have a common vertex O and a common arm.
So, $\angle A$ and $\angle B$ are adjacent angles.
3. Which angles are adjacent angles to $\angle BOC$?
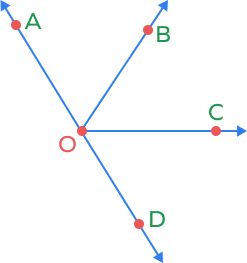
Solution:
We know that adjacent angles share a common vertex and a common side.
$\angle AOB$ is adjacent to $\angle BOC$ with common vertex O and common arm OB.
$\angle COD$ is adjacent to $\angle BOC$ with common vertex O and common arm OC.
4. Observe the given diagram. Which angles are adjacent angles?
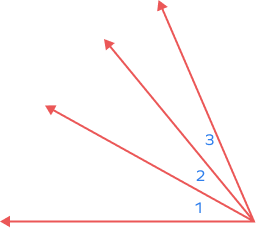
Solution:
Angles 1 and 2 are adjacent.
Angles 2 and 3 are adjacent.
Also, observe that the angle formed by combining the angles 1 and 2 together is adjacent to angle 3.
Angle formed by combining angles 2 and 3 together is adjacent to angle 1.
5. Name the pairs of adjacent angles.
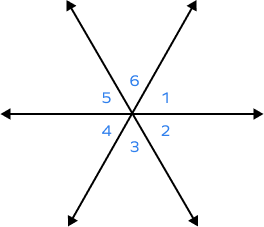
Solution:
We know that adjacent angles share a common vertex and side.
The pair of adjacent angles are:
$\angle 1$ and $\angle 2$
$\angle 2$ and $\angle 3$
$\angle 3$ and $\angle 4$
$\angle 4$ and $\angle 5$
$\angle 5$ and $\angle 6$
$\angle 1$ and $\angle 6$
Practice Problems on Adjacent Angles
Adjacent Angles: Definition, Properties, Examples, Facts, FAQs
Adjacent angles share ___________.
Adjacent angles share a common vertex and a common side.
Angles a and b in the given diagram are ______
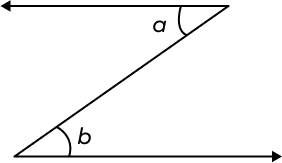
Angles a and b are nonadjacent angles since they only share a common side and not a common vertex.
In the following image, $\angle AOB$ is adjacent with _____.
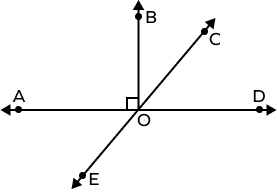
$\angle AOB$ is adjacent with $\angle BOC$, $\angle AOE$, and $\angle BOD$. It shares a common arm and a common vertex with each of these angles.
Vertical angles share a common ________.
Vertical angles share a common vertex but not a common side.
What are the adjacent angles to $\angle 1$?
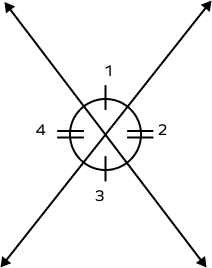
The angles adjacent angles to $\angle 1$ are $\angle 2$ and $\angle 4$.
Which of the following are not adjacent angles?
$\angle BCD$ and $\angle BCE$ are not adjacent since $\angle BCD$ overlaps $\angle BCE$.
Frequently Asked Questions about Adjacent Angles
Can vertical angles ever be adjacent?
No, vertical angles can never be adjacent. Vertical angles only share a common vertex while being the opposite of one another. Adjacent angles are the ones next to each other, sharing common vertex and side, while vertical angles are opposite from each other.
Are the angles forming a linear pair adjacent angles?
Angles forming a linear pair are always adjacent to each other.
What are the angles formed by two intersecting lines?
When two lines intersect, they form different types of angles such as vertical angles, adjacent angles, angles in linear pairs.
Can two adjacent angles overlap?
No, adjacent angles never overlap. If one angle is contained in another, then the two angles are not adjacent. It is one of the major properties of adjacent angles.
Do adjacent angles add up to 180 degrees?
Adjacent angles need not add up to 180 degrees. The sum of adjacent angles will be 180 degrees if and only if they form a linear pair.





























