What Are Alternate Interior Angles in Geometry?
When a transversal crosses two parallel lines (or non-parallel lines), the pair of nonadjacent angles formed on the inner side of the parallel lines, but on the opposite sides of the transversal are known as alternate interior angles.
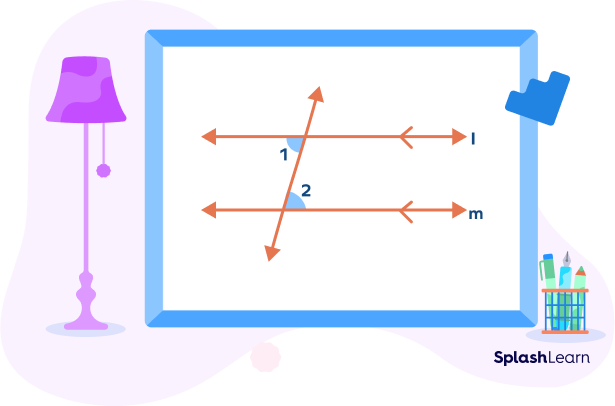
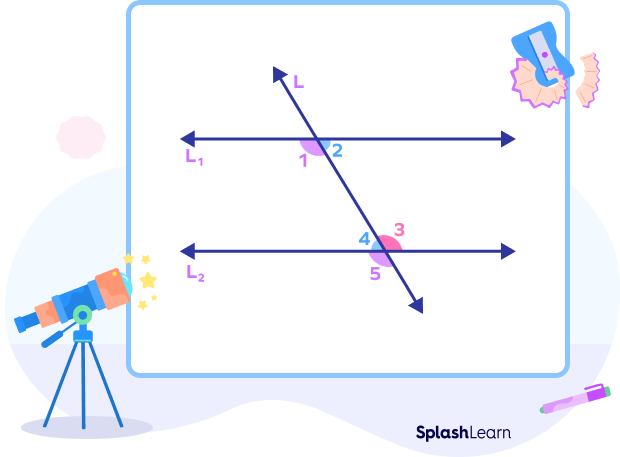
The following diagram shows alternate interior angles formed in two cases:
i) parallel lines cut by a transversal
ii) non-parallel lines cut by a transversal.
Alternate interior angles are:
- ∠2 and ∠3
- ∠1 and ∠4
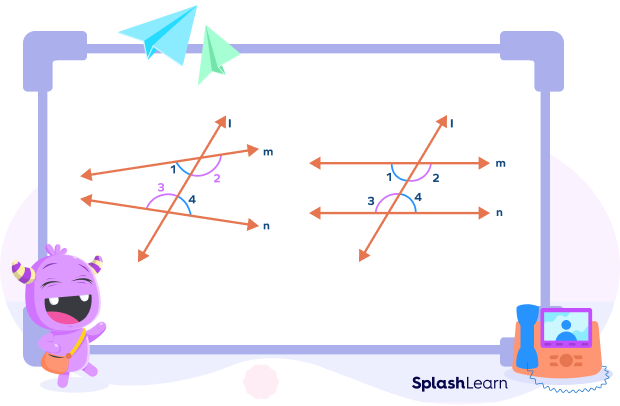
If the lines are parallel, the alternate interior angles are always equal. In other words, the alternate interior angles can be used to prove whether the lines given are parallel or not. If the alternate interior angles are equal, then the given lines that are crossed by a transversal are said to be parallel.
Recommended Games
Alternate Interior Angles: Definition
A pair of nonadjacent angles formed on the alternate side of the transversal but lying in between the two lines cut by the transversal are called alternate interior angles.
Recommended Worksheets
How to Find the Alternate Interior Angles
It is very easy to locate or identify the alternate interior angles due to their position. They together make a Z-shape or Z-pattern. They lie in the interior region between two lines, but on the opposite side of the transversal.
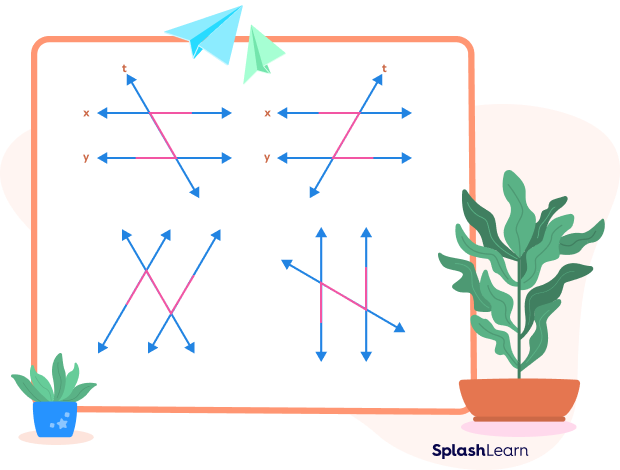
Properties of Alternate Interior Angles
- When two parallel lines cut by a transversal, the alternate Interior angles formed are congruent.
- They share one common arm. They do not share a common vertex.
- Alternate interior angles don’t have any specific properties in case of non – parallel lines.
- If two non-parallel lines are cut by a transversal, the alternate Interior angles formed are not congruent.
Alternate Interior Angles Theorem and Proof
Statement: If a transversal crosses two or more parallel lines, the alternate interior angles are congruent.
Given: a ∥ d
To prove: ∠4 = ∠5 and ∠3 = ∠6
Proof: Suppose line x is parallel to line y, and t is the transversal.
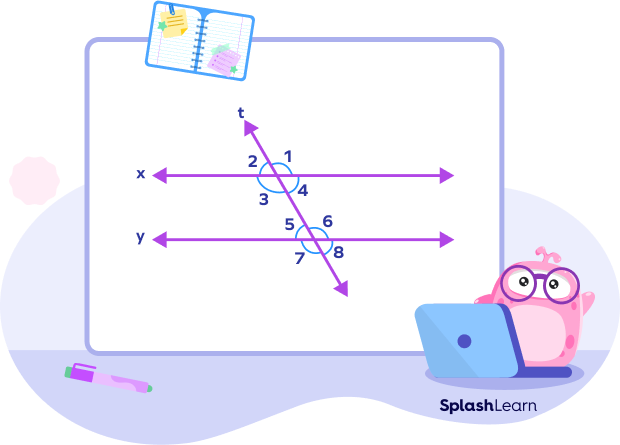
We know that if a transversal cuts any two parallel lines, the corresponding angles and vertically opposite angles are equal to each other. Therefore,
m∠2 = m∠5 ………..(i) [Corresponding angles]
m∠2 = m∠4 ………..(ii) [Vertically opposite angles]
From (i) and (ii), we get
m∠4 = m∠5
Similarly,
m∠3 = m∠6
Hence, proved.
Converse of the Alternate Interior Angles Theorem
Statement: If a transversal intersects two lines such that the alternate interior angles are equal, then the two lines are parallel.
m∠1 = m∠3 (given)
m∠3 = m∠5 (vertically opposite angles)
Hence, m∠1 = m∠5. (by transitive property of equality)
Similarly, we can prove that ∠2 = ∠4.
However, the angle pairs ∠1-∠5 and ∠2-∠4 are pairs of corresponding angles.
By the converse of the corresponding angles postulate, lines are parallel to each other.
Facts about Alternate Interior Angles
- Alternate interior angles are a pair of non-adjacent angles that are located on opposite sides of the transversal and inside the two parallel lines.
- Alternate interior angles formed by parallel lines cut by a transversal are always congruent.
Conclusion
In this article, we learned about Alternate Interior Angles. We discussed important definitions and theorems associated with alternate interior angles. Let’s solve a few examples and MCQs for hands-on practice!
Solved Examples on Alternate Interior Angles
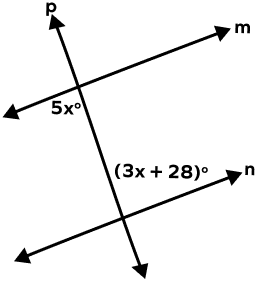
1. Find the measure of x in the following figure.
Solution:
m ∥ n and p is the transversal.
The given angles are alternate interior angles.
(5x)° = (3x + 28)°
(5x – 3x)° = 28°
(2x)° = 28°
x = 14
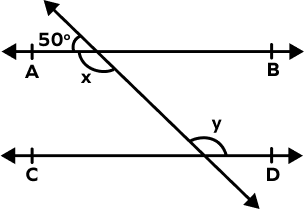
2. Find the value of x and y in the following figure.
Solution:
x + 50° = 180° (Angles in a linear pair.)
x = 180° – 50°
x = 130°
AB ∥ CD and t is the transversal.
y = x = 130° (Alternate interior angles.)
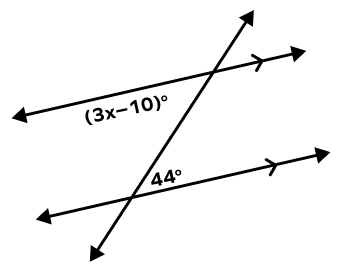
3. What is the value of x in the following figure?
Solution:
Two parallel lines are cut by a transversal. The given two angles are alternate interior angles. Thus, they are congruent.
(3x – 10) = 44
3x = 44 + 10
3x = 54
x = 18
4. What is the measure of angles 1, 3, and 4?
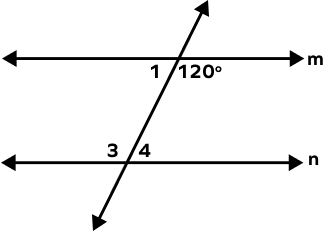
Solution:
m || n and l is the transversal.
m∠3 = 120° (Alternate Interior Angles)
m∠3 + m∠4 = 180° (Angles in a linear pair)
120° + m∠4 = 180°
m∠4 = 60°
Similarly, m∠1 + 120° = 180° (Angles in a linear pair)
m∠1 = 60°
Practice Problems on Alternate Interior Angles
Alternate Interior Angles - Definition, Theorems, Examples, Facts
The alternate interior angles formed when two parallel lines are cut by a transversal are
According to the Alternate Interior Angles Theorem, the alternate interior angles are equal when two parallel lines are cut by a transversal.
The alternate interior angles are formed on the _______ of the transversal.
The alternate interior angles are formed on the opposite of the transversal and in the alternate positions in the interior region of the parallel lines.
The alternate interior angles form a _______ pattern.
Alternate interior angles form a Z-shaped pattern.
Find the value of z in the following figure.
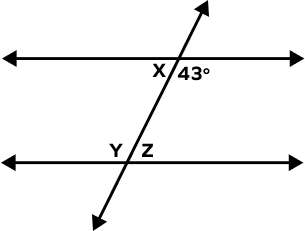
x + 43° = 180° (Linear Pair)
x = 180° – 43° = 137°
Now,
x = z (Alternate Interior angles)
z = 137°
Frequently Asked Questions about Alternate Interior Angles
Are alternate iInterior angles supplementary?
The alternate interior angles formed when two parallel lines are crossed by a transversal are congruent, not supplementary.
What is the other name for Alternate Interior Angles?
The other name for Alternate Interior Angles is ‘Z’ Angles as they form a Z.
Are alternate interior angles always equal?
No, alternate interior angles are not always equal. They are equal only when the lines are parallel.
What are co-interior angles?
Co-interior angles or same-side interior angles are the pair of angles formed on the same side of the transversal and in the interior region of the two parallel lines.





























