In geometry, parallel lines can be defined as two lines in the same plane that are at equal distance from each other and never meet. They can be both horizontal and vertical.
We can see parallel lines examples in our daily life like a zebra crossing, the lines of notebooks, and on railway tracks around us.

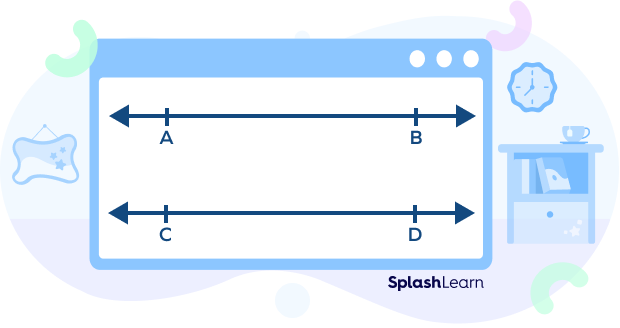
What Do Parallel Lines Look Like?
In the figure below, line “AB” is parallel to the line “CD”.
The perpendicular distance is always the same between two parallel lines.
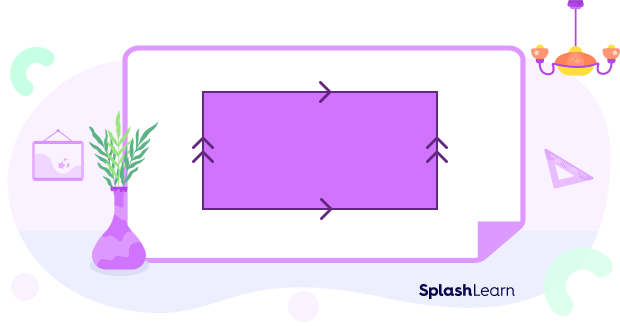
Sides of various shapes are parallel to each other. In the rectangle given below, the single arrow lines are parallel to each other, and similarly, the double arrow lines are also parallel to each other.
Parallel lines are represented with a pair of vertical lines between the names of the lines, using the sign: ︳︳
Recommended Games
Let’s Sing!
Draw parallel lines on a sheet,
Use a ruler to make them neat!
Make sure their ends never meet!
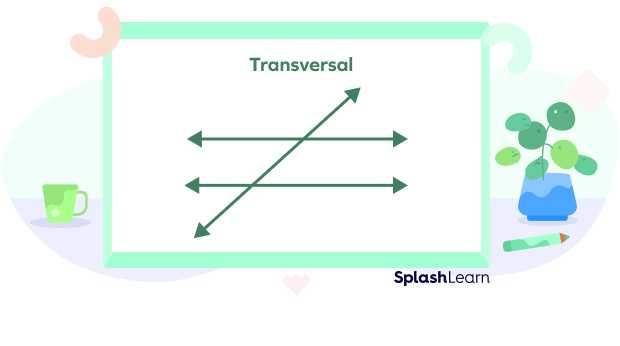
What Is a Transversal?
A transversal is a line that intersects two parallel lines (or lines on a plane) at different intersecting points, forming angles.
Properties of Parallel Lines
Parallel lines can be easily identified using the following fundamental properties and characteristics:
- They are always straight lines with an equal distance between each other.
- They are coplanar lines.
- They never intersect, no matter how far you try to extend them in any given direction.
- If there is a transversal line that intersects two parallel lines at two different points, it will form 4 angles at each point.
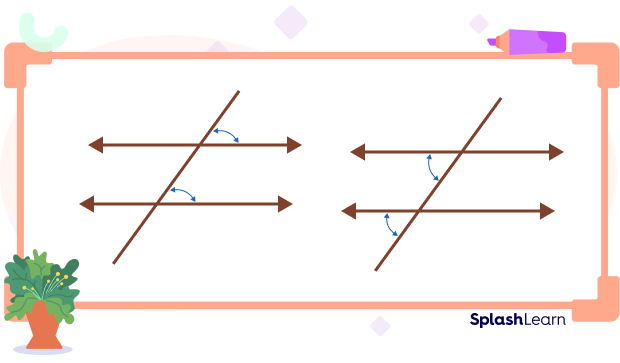
- The corresponding angles formed by the two parallel lines and a transversal are equal.
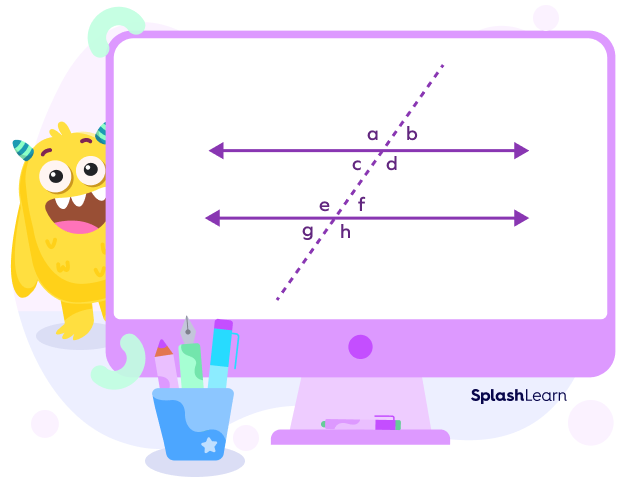
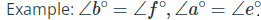
- Pairs of internal angles on the same side of the crossing are supplementary.
- The vertically opposite angles/apex angles are equal.
- Alternate internal/interior angles are equal.
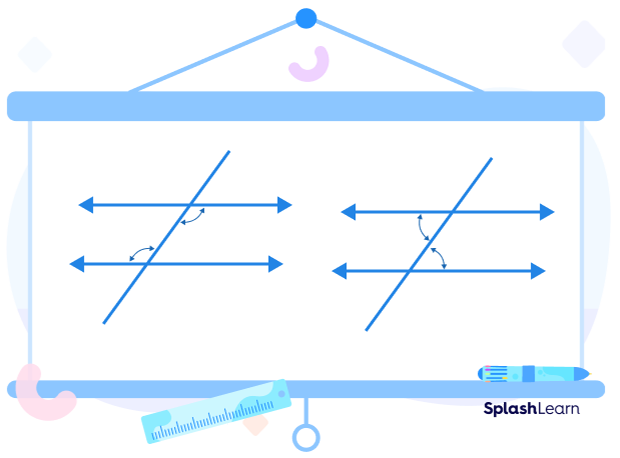
- Alternate external/exterior angles are also equal.
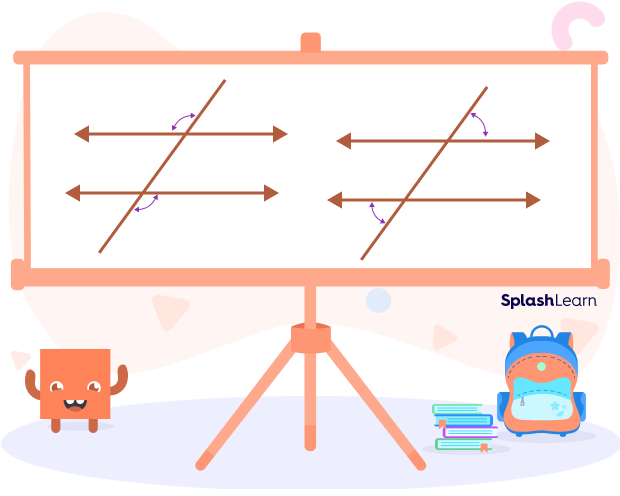
Parallel Line Equations
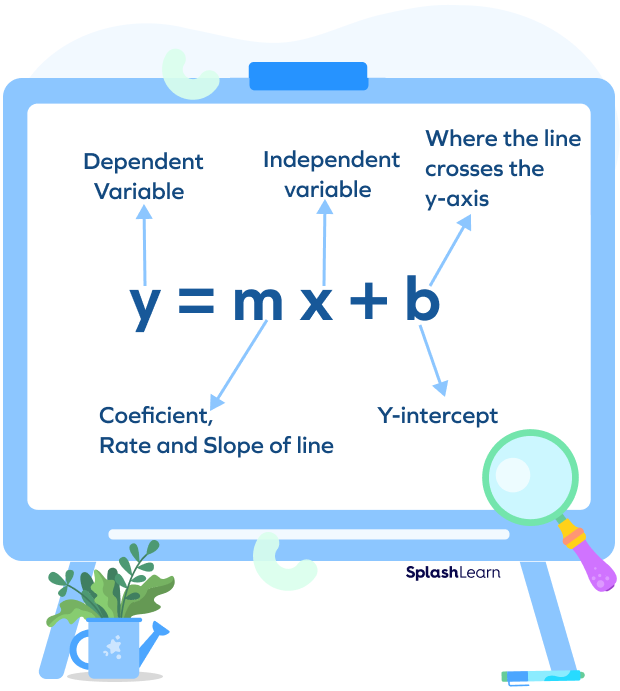
Linear equations are generally described by the slope-intercept represented by the equation $y = mx + b$.
Where “m” is the slope, “b” is the y-intercept, and y and x are variables.
The value of “m” determines the slope and indicates the steep slope of the line.
Note that the slopes of the two parallel lines are always the same.
For example, if the slope of the straight line in the equation y $= 4x + 3$ is 4, then all lines parallel to $y = 4x + 3$ have the same slope, or 4.
Parallel lines have different y-intersections and have no points or angles in common.
Solved Examples on Parallel Lines
Example 1: Find out which lines are parallel to each other in the given figure.
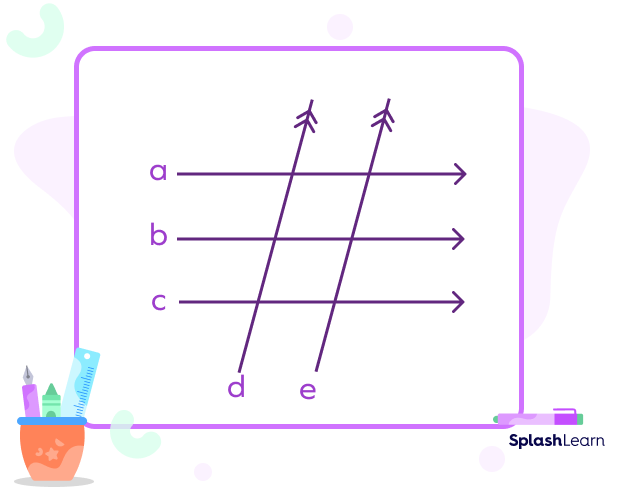
Solution: All the three lines with arrows passing through them are parallel to each other, which means:
a || b || c
Lines with the double arrows, i.e., line d and e are transversals of lines a, b, and c, but they are parallel to each other.
So, we can say that d || e
Example 2: Find whether the given lines intersected by a transversal in the figure are parallel or not.
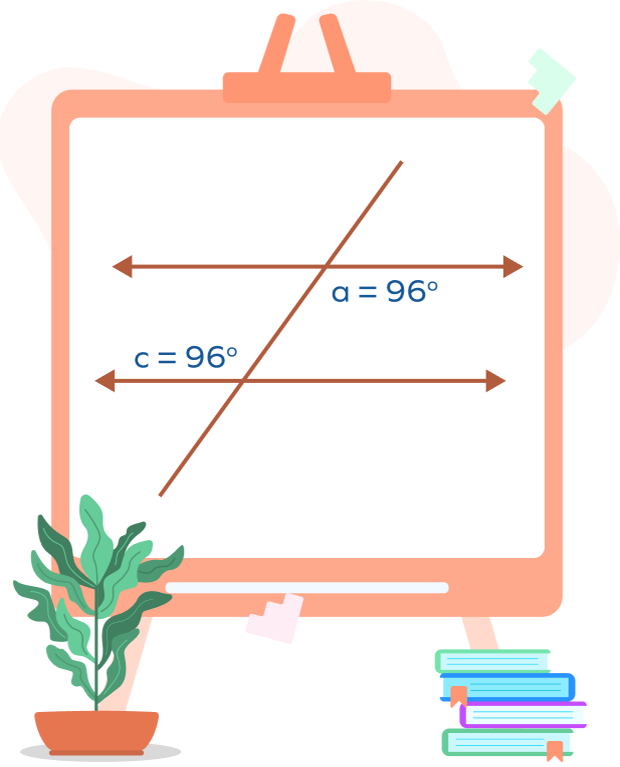
Solution: The two lines are parallel as they meet one of the properties of parallel lines “when the alternate interior angles are equal, the lines are parallel”.
$∠a$ is equal to $∠c$, and both of these are alternate interior angles.
This proves that the two lines are parallel.
Example 3: Are the lines intersected by the transversal in this figure parallel?
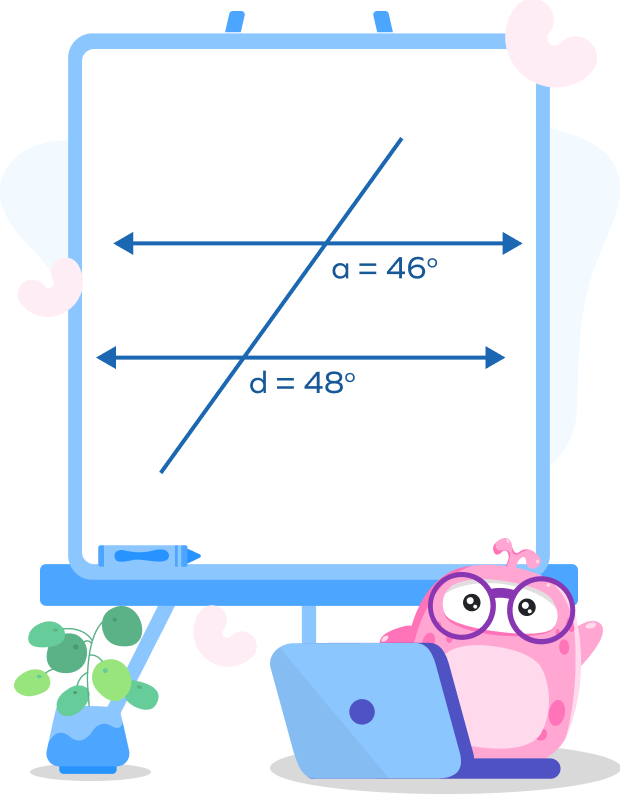
Solution: According to the given properties of parallel lines, the alternating, corresponding, and consecutive angles should be the same to form parallel lines.
In this case, $∠a$ is not equal to $∠d $
Thus, these two lines are not parallel.
Practice Problems on Parallel Lines
Parallel Lines - Definition With Examples
Which of the following terms does not describe a pair of parallel lines?
According to the definition of parallel lines, they are coplanar lines that are evenly
spaced but never intersect. This indicates that parallel lines are not noncoplanar.
Which of the following real-world examples does not represent a pair of parallel lines?
The wiper of a car, stairs, railings, and the strings of a racket all have the same orientation and do not intersect. They are all in the same plane (that is, the strings are in the same plane in the net).
However, the hands of the clock intersect at the center of the clock and are not represented by a pair of parallel lines.
A transversal intersects these two parallel lines. If the value for one angle is given, can you find the value of ∠X?
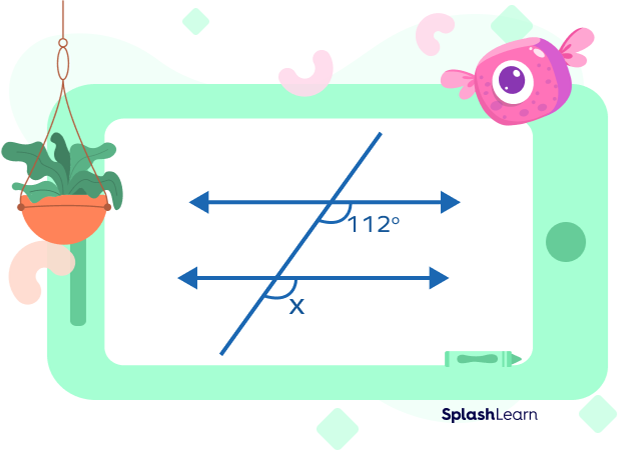
If both the lines are parallel, then according to one of the properties of parallel lines, the corresponding angles and alternating interior and exterior angles formed are equal.
In this case, as the alternate exterior angles will be equal,
$∠X = 112°$ as given.
Frequently Asked Questions on Parallel Lines
What are the different types of parallel lines?
Parallel lines can be vertical, diagonal, and horizontal.
How are parallel lines used in coordinate geometry?
If the graphs of two linear equations of coordinate geometry are parallel, then the two equations have no common solution.
The slopes of two parallel lines are the same and always equal in coordinate geometry.
How can you prove that two lines are parallel?
You can use some geometric relationships to prove that two lines are parallel.
A transversal is a line that intersects two or more lines. When a line intersects a pair of parallel lines, a pair of different angles are formed.
These different types of angles are used to prove whether the two lines are parallel to each other according to the given properties of parallel lines.


























