What Is Angle Bisector Theorem?
Angle bisector theorem states that an angle bisector divides the opposite side into two line segments that are proportional to the other two sides.
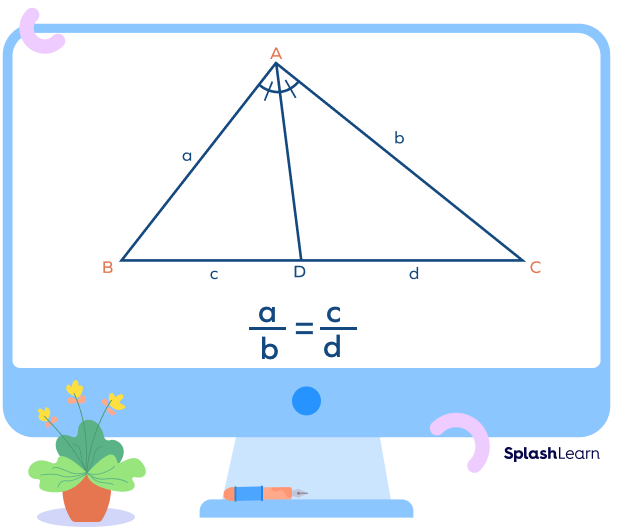
Here, in $\Delta ABC$, the line AD is the angle bisector of $\angle A$.
AD bisects the side BC in two parts, c and d.
a and b are the lengths of the other two sides.
By the angle bisector theorem, we have
$\frac{a}{b} = \frac{c}{d}$
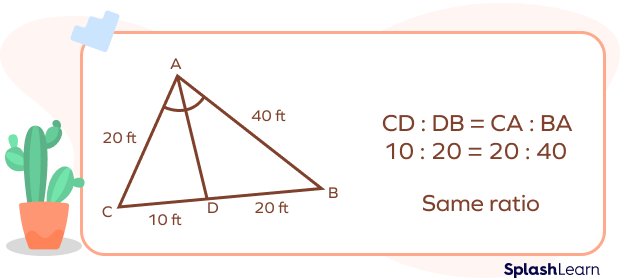
Consider an example:
Recommended Games
Angle Bisector Theorem Statement
The bisector of an interior angle of a triangle divides the opposite side internally in the ratio of the corresponding sides containing the angle.
Recommended Worksheets
Interior Angle Bisector Theorem
The interior angle bisector theorem is simply referred to as angle bisector theorem. Hence, an interior angle bisector of a triangle divides the opposite side in two parts such that the ratio of the two line segments is proportional to the ratio of the other two sides.
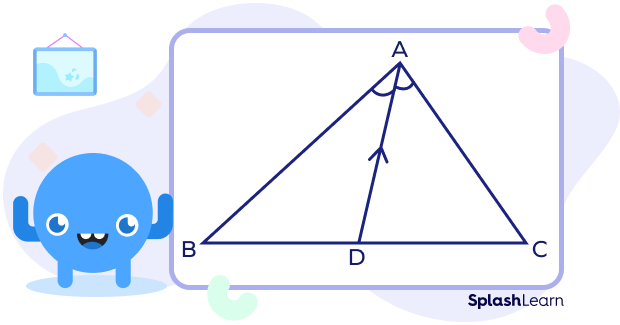
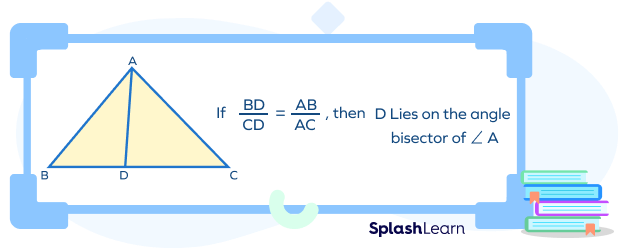
Let us consider $\Delta ABC$ as shown above. Here, AD is the angle bisector (interior angle bisector) of $\angle BAC$, which meets the opposite side BC at point D. Hence, as per this theorem, the ratio of the BD to DC is equal to the ratio of the lengths of other sides, AB to AC.
$\frac{BD}{DC} = \frac{AB}{AC}$.
External Angle Bisector Theorem
A triangle’s external angle bisector divides one side externally in proportion to the ratio of the sides containing the angle. Most of the time, non-equilateral triangles have this condition.
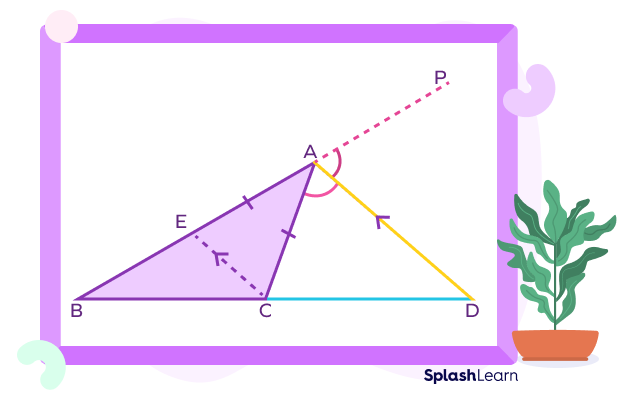
Let us consider $\Delta ABC$ as shown above.
The side AB is extended. $\angle CAP$ is an external angle.
Here, AD is the angle bisector (exterior angle bisector) of $\angle CAP$.
CE is drawn parallel to DA, such that it meets the line AB of a triangle at E.
Hence, according to the external angle bisector theorem:
$\frac{BD}{DC} = \frac{AB}{AC}$
Angle Bisector Theorem Proof
Statement: The angle bisector of a triangle divides the opposite side in such a way that the ratio of the two line segments is proportional to the ratio of the other two sides.
Let’s prove this statement.
Given: Let us consider $\Delta ABC$, in which AD is the angle bisector of $\angle BAC$, which meets BC at point D.
To prove: $\frac{BD}{DC} = \frac{AB}{AC}$.
Construction: Draw a ray CE parallel to DA. Extend BA such that it intersects CE at E.
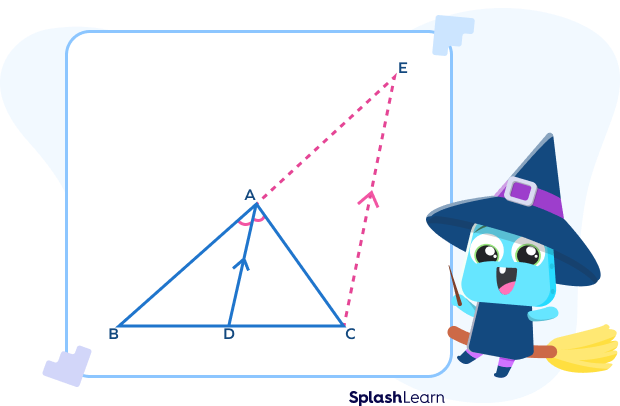
Since $CE || DA$, AC acts as the transversal.
$\angle DAC = \angle ACE$ (alternate interior angles) …(1)
$\angle BAD = \angle AEC$ (corresponding angles) …(2)
As we know that AD is the angle bisector of $\angle BAC$,
$\angle BAD = \angle DAC$ …(3)
From (1), (2) and (3), we have
$\angle ACE = \angle AEC$ this implies that $\Delta ACE$ is an isosceles triangle.
Therefore, opposite sides of equal angles are equal.
Thus for $\Delta ACE$, we can write,
$AE = AC$ …(4)
Now, in $\Delta BCE$ we have, $CE || DA$.
By triangle proportionality theorem, a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally.
$\frac{BD}{DC} = \frac{AB}{AE}$ …(5)
From equation (4) we have $AE = AC$, so on replacing AE by AC in equation (5), we get
$\frac{BD}{DC} = \frac{AB}{AC}$
Hence, the angle bisector theorem is proved.
Converse of Angle Bisector Theorem
The converse of the angle bisector theorem states that if the interior point of an angle of a triangle is equidistant from the two sides (arms) of a triangle, then that point lies on the angle bisector of the angle.
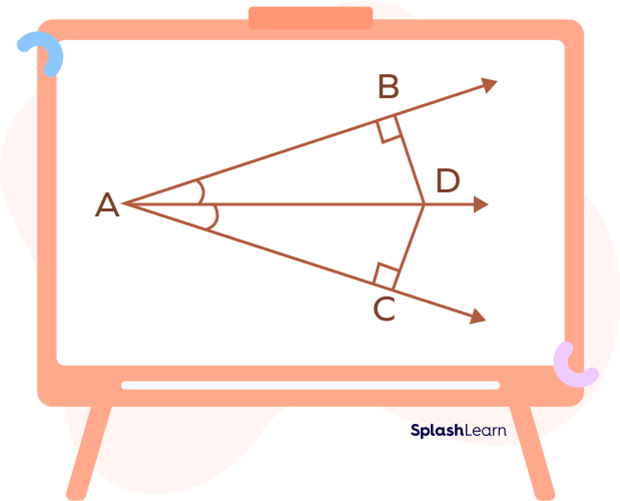
D is a point in the interior of $\angle BAC$.
If the perpendicular distances BD and DC are equal then, the line AD is the angle bisector of angle $\angle BAC$.
If $BD = CD$, then $\angle BAD = \angle CAD$.
Facts about Angle Bisector Theorem
- The points on an angle bisector are all equidistant from the arms of the angle.
- In real life, angle bisectors have applications in games of billiards, rugby, football, architecture, etc.
- Angle bisector theorem helps to find unknown lengths of sides of a triangle.
- The point of concurrency of the angle bisectors of a triangle is known as the incenter of a triangle.
Conclusion
In this article, we learned about angle bisector theorem, its proof, interior angle bisector and exterior angle bisector theorem, the converse of angle bisector theorem, and application of these theorems in problem-solving as well in real life.
Solved Examples on Angle Bisector Theorem
- In the figure given below, find the ratio AD:DC.
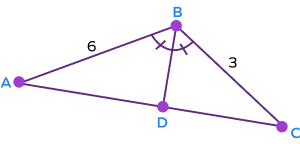
Solution:
$AB = 6,\; BC = 3$.
Also, BD is the angle bisector.
According to the angle bisector theorem, BD divides AC in the ratio proportional to the ratio of the other two sides.
Thus, the ratio of AD to DC is the same as the ratio of AB to BC.
$\frac{AB}{BC} = \frac{AD}{DC}$
$\Rightarrow \frac{6}{3} = \frac{AD}{DC}$
$\Rightarrow AD:DC = 6:3$
$\Rightarrow AD:DC = 2:1$
- In the figure given below, if PS is the angle bisector, find the length of segments RS and QS.
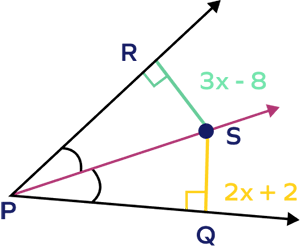
Solution:
RS $= 3x \;-\; 8,\; SQ = 2x + 2$
From the figure, point S lies on the bisector of angle QPR.
Thus, the point S is equidistant from the sides PR and PQ.
RS $= SQ$
$\Rightarrow 3x\;-\;8 = 2x + 2$
$\Rightarrow 3x\;-\;2x = 2 + 8$
$x = 10$
RS $= 3x\;-\;8 = 3(10)\;-\;8 = 22$
SQ $= 2x + 2 = 2(10) + 2 = 22$
$\therefore$ RS $= SQ = 22$ units.
- In $\Delta PQR$ as shown below, PS is the angle bisector of $\angle P$. Find the lengths of sides of ΔPQR.
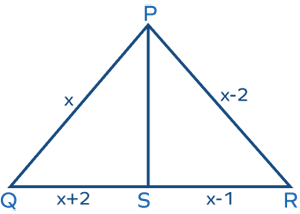
Solution:
According to the angle bisector theorem, $\frac{PQ}{PR} = \frac{QS}{SR}$
$\Rightarrow \frac{x}{x \;-\; 2} = \frac{x + 2}{x \;-\; 1}$
$\Rightarrow x(x\;-\;1) = (x\;-\;2)(x + 2)$
$\Rightarrow x^2\;-\;x = x^2\;-\;4$
$\Rightarrow \;-\;x = \;-\;4$
$\Rightarrow x = 4$
Hence, length of the sides are
PQ $= x = 4$,
PR $= x\;-\;2 = 4\;-\;2 = 2$,
QR $= (x + 2) + (x\;-\;1) = 2x + 1 = 2(4) + 1 = 9$.
Practice Problems on Angle Bisector Theorem
Angle Bisector Theorem: Definition, Formula, Proof, Examples
If the time on a clock is exactly 04:00, then where should the bisector of the hour hand and minute-hand point?
If the time on a clock is exactly 04:00, then the angle bisector and it points to 2.

Which of the following options represent the statement of angle bisector theorem for the given triangle?
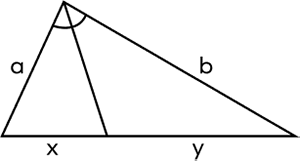
According to the angle bisector theorem, $\frac{a}{b} = \frac{x}{y}$.
The __________ of a triangle divides the opposite sides in the ratio equal to the ratio of the remaining two sides.
An angle bisector divides the opposite side into two line segments that are proportional to the remianing two sides.
The bisectors of the angles of a triangle are _________.
The bisectors of the angles of a triangle pass through a common point. Hence, bisectors of the angles of a triangle are concurrent.
Frequently Asked Questions on Angle Bisector Theorem
What is the chord bisector theorem?
The perpendicular drawn from the center of a circle to a chord bisects the chord.
Is the angle bisector theorem and triangle angle bisector theorem the same?
Yes, the angle bisector theorem is also known as the triangle angle bisector theorem.
What is the exterior angle bisector theorem?
According to the exterior angle bisector theorem, a triangle’s external angle bisector divides one side externally in proportion to the ratio of the sides containing the angle.
What is the converse of the angle bisector theorem?
The converse of the angle bisector theorem states that the point on the opposite side of an angle is assumed to be on its angle bisector if the sides of a triangle satisfy the following condition: “If a line drawn from a vertex of a triangle divides the opposite side into two parts such that they are proportional to the other two sides of the triangle.”
How to apply the triangle angle bisector theorem?
The missing lengths of a triangle’s sides can be determined by applying the triangle angle bisector theorem. Let $\angle A$ be divided by the bisector AD. Hence, according to the triangle angle bisector theorem $\frac{BD}{DC} = \frac{AB}{AC}$.





























