Area of Trapezium – Definition, Formulas, Derivation, Facts, FAQs

What Is the Area of Trapezium?

The area of trapezium is the region covered by a trapezium in 2D plane. It is measured in square units. It is given by

Area of Trapezium $= \frac{1}{2}\times$ Sum of parallel sides $\times$ height

A trapezium (also known as trapezoid in the US) is a 2D shape. To be more specific, it is a quadrilateral as it has 4 sides.

Observe the given diagram. 

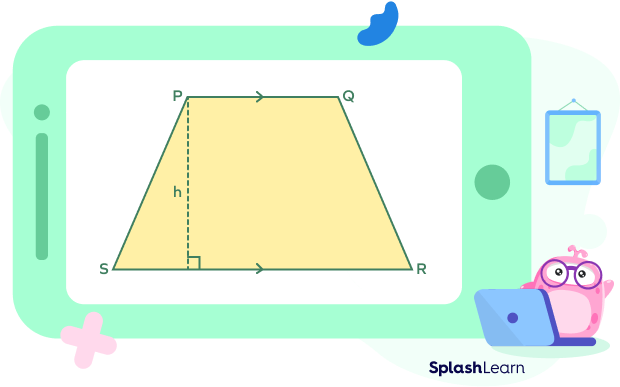
Here are the important parts and terms related to the trapezium PQRS.  

• Bases of the trapezium: the parallel sides (PQ || RS)
• Legs of the trapezium: The non-parallel sides (PS and QR) 
• Altitude or height of the trapezium: The perpendicular distance between the two parallel sides 

Here, the area of trapezium is the shaded region. The area of trapezium depends on the lengths of the parallel sides and the height.

Area of Trapezium Formula

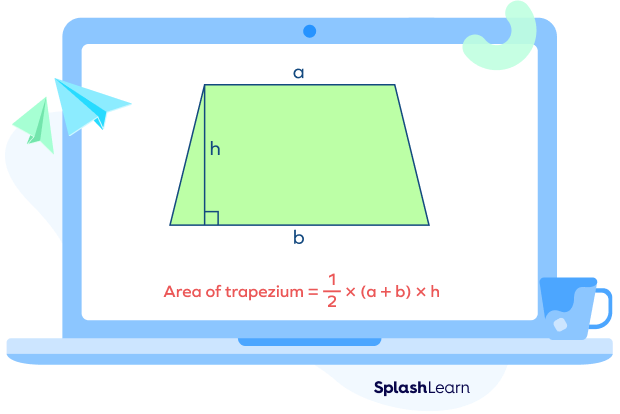
The formula to calculate the area of the trapezium is given as

Area of trapezium $= \frac{1}{2} \times (a + b)\times h$

where

a and b are the lengths of parallel sides, 

h is the height (perpendicular distance between the parallel sides) 

How to Derive the Area of Trapezium Formula

Let’s understand the derivation of the formula or equation for the area of trapezium. 

Consider a trapezium ABCD. To find the area of trapezium ABCD, we will divide it into two right triangles and a rectangle, since we know how to calculate the area of these shapes. 

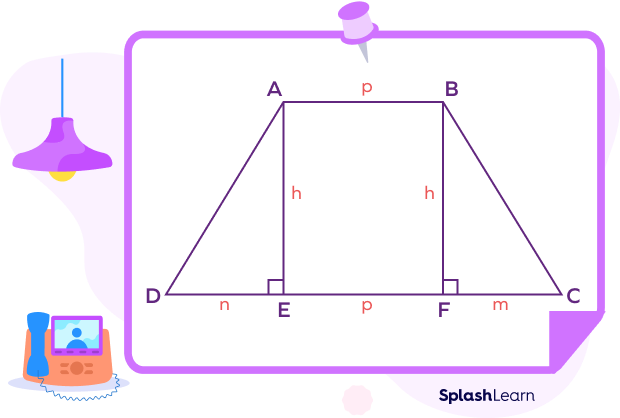
Construction:

• Draw a perpendicular AE such that we get a right-angled triangle △ AED with DE = n units and AE = h units
• Draw a perpendicular BF such that △BFC is a right-angled triangle with FC = n units and BF = h units

Note that AEFB is a rectangle formed such that AE = BF = h units and AB = EF = p units.

Area of trapezium ABCD = Area of △AED + Area of the rectangle AEFB + Area of △ BFC

Area of a triangle is given by 

Area of triangle $= \frac{1}{2} \times$ base $\times$ height

Area of ADE $= \frac{1}{2} \times n \times h$ ———- (i)

Area of BFC $= \frac{1}{2} \times m \times h$ ———- (ii)

Area of the rectangle is given by 

Area of rectangle $=$ length $\times$ breadth 

So, the area of the rectangle AEFB is 

Area of AEFB $= p \times h$ ———- (iii)

By adding equations (i), (ii), and (iii), we have 

Area of trapezium ABCD $= (\frac{1}{2} \times n \times h) + (\frac{1}{2} \times m \times h) + (p \times h)$

Area of trapezium ABCD $= \frac{nh}{2} + \frac{mh}{2} + ph$

Area of trapezium ABCD  $= \frac{nh + mh + 2ph}{2}$

Area of trapezium ABCD $= \frac{1}{2} \times h \times \left[p + (p + n + m)\right]$ —— (v)

Here, we notice that

CD $= p + n + m$ 

AB$ = p$

Put the value of q in equation (v). 

Area of trapezium ABCD $= \frac{1}{2} \times [AB + CD] \times h$

Area of trapezium ABCD $= \frac{1}{2} \times$ Sum of parallel sides$\times$ height

How to Find the Area of Trapezium

Step 1: Note down the dimensions, such as the lengths of the bases (parallel sides) and the height of the trapezium. Make sure that the dimensions of the trapezium are in the same units. If the dimensions are in different units, then convert them to the same unit.

Step 2: Calculate the sum of the bases. Multiply the sum by the height.

Step 3: Multiply the product obtained in Step 2 by $\frac{1}{2}$ or you can divide the product by 2.

Step 4: Write the area in square units (inches², feet², etc.). 

Let’s understand how to find the area of trapezium with an example:

Example: What is the area of trapezium ABCD? 

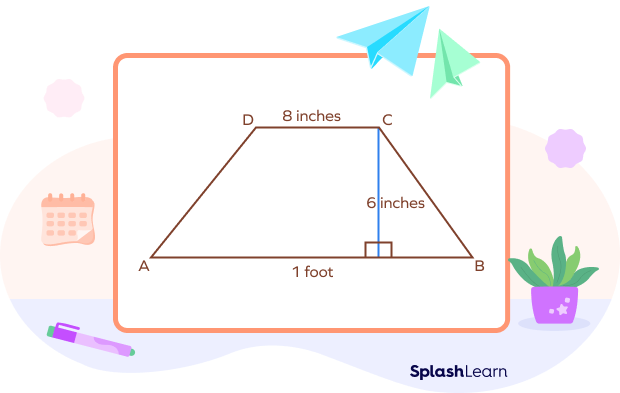
Solution:

AB = a = 1 foot 

CD = b = 8 inches

Height = h = 6 inches

Since the dimensions are not in the same unit, we need to convert them to one unit. 1 foot = 12 inches

Therefore, a = 12 inches

Area of trapezium $= \frac{1}{2} \times (a + b) \times h$

Area of trapezium $= \frac{1}{2} \times (12 + 8) \times 6$

Area of trapezium $= \frac{1}{2} \times 20 \times 6$

Area of trapezium $= 60$ square inches

Facts about Trapezium

Conclusion

A trapezium is a simple yet interesting shape in geometry. The concept of the area of trapezium is used in many physics concepts and also in construction projects. Get a better grasp of the concept with the help of examples and practice questions and excel in your math tests.

Solved Examples on the Area of Trapezium

1. A trapezium has base lengths a = 22 inches and b = 26 inches respectively. The distance between them is 18 inches. Find the area of trapezium. 

Solution:

a = 22 inches

b = 26 inches

Distance between parallel sides = h = 18 inches

Area of trapezium $= \frac{1}{2} \times (a + b) \times h$

Area of trapezium $= \frac{1}{2} \times (22 + 26) \times 18$

                              $= \frac{1}{2} \times 48 \times 18$

Area of trapezium $= 432$ inches²

2. The area of the given trapezium is 352 feet². Find the value of a. 

Solution:

a = ?

b = 25 feet

h = 16 feet

Area of trapezium = 352 square feet

Area of trapezium $= \frac{1}{2} \times (a + b) \times h$

$352 = \frac{1}{2} \times (a + 25) \times 16$

$(a + 25) = \frac{352 \times 2}{16}$

$(a + 25) = 44$

a = 19 inches

3. Find the altitude of a trapezium whose area is 85 feet² and the length of the parallel sides are 15 feet and 25 feet, respectively. 

Solution:

Using the value of the area of a trapezium when height is not given, the calculations will be as follows:

a = 15 feet 

b = 25 feet

Area = 85 feet²

Area of trapezium $= \frac{1}{2} \times (a + b) \times h$

$85 = \frac{1}{2} \times (15 + 25) \times h$

$h =  \frac{85\times 2}{(15 + 25)}$

$h = \frac{85\times 2}{40}$

h = 4.25 feet

Therefore, the altitude is 4.25 feet.

4. The area of a trapezium is 360 inches², and the distance between its sides is 20 inches. If the length of one of the sides is 15 inches, find the length of the other side.

Solution: 

a = 15 inches

h = 20 inches

Area = 360 inches²

Let the other side be x inches 

Area of trapezium $= \frac{1}{2} \times (a + b) \times h$

$360 = \frac{1}{2} \times (15 + x) \times 20$

$360 = (15 + x) \times 10$

$360 = 150 + 10x$

$10x = 360 \;-\; 150$

$x =  \frac{210}{10}$

x = 21 inches

Therefore, the other side of the trapezium is 21 inches.

5. The length of the two bases of a trapezium is in the ratio 5:2, and the height between them is 10 inches. If the area of the trapezium is 350 inches², find the length of the parallel sides.

Solution:

Let the length of the sides be a = 5x, b = 2x.

h = 10 inches

Area = 350 inches² 

Area of trapezium $= \frac{1}{2} \times (a + b) \times h$

$350 = \frac{1}{2} \times (5x + 2x) \times 10$

$350 = 7x \times 5$

$350 = 35x$

$x = \frac{350}{35}$

$x = 10$

Therefore, 

$a = 5x = 5 \times 10 = 50$ inches 

$b = 2x = 2 \times 10 = 20$ inches 

Practice Problem on Area of Trapezium

Frequently Asked Questions about the Area of Trapezium