- What Is the Area of a Triangle in Determinant Form?
- Formula of Area of Triangle in Determinant Form
- How to Determine the Area of Triangle in Determinant Form
- Solved Examples on Area of Triangle in Determinant Form
- Practice Problems of Area of Triangle in Determinant Form
- Frequently Asked Questions about the Area of Triangle in Determinant Form
What Is the Area of a Triangle in Determinant Form?
In coordinate geometry, the area of a triangle in determinant form can be calculated when the coordinates of the vertices of the triangle are provided. Calculating the area of a triangle in determinant form is an important application of determinants.
If the vertices of a triangle PQR are P(x1, y1), Q(x2, y2), and R(x3, y3), the area of the triangle can be calculated as follows:
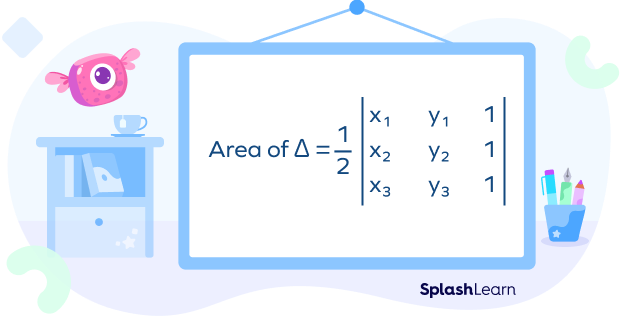
Note that the process of expanding to find the determinant of a matrix remains consistent regardless of the chosen row or column. The result remains the same, making the choice of row or column arbitrary.
Expanding the determinant along the first column, we get
Area $= \frac{1}{2} \times \left[x_{1} (y_{2} – y_{3}) + x_{2} (y_{3} – y_{1}) + x_{3} (y_{1} – y_{2})\right]$
A determinant of a square matrix A is a real value denoted by | A | or det (A). It is a scalar value held by every square matrix.

Recommended Games
Formula of Area of Triangle in Determinant Form
Normally, the area of a triangle is calculated using the formula $\frac{1}{2} \times b \times h, where b is the base and h is height of the triangle.
Some cases, however, use a different formula for determining the triangle’s area where the height is not given. The vertices of the triangle are employed for the evaluation of the area using the following determinant formula.
Suppose a triangle ΔPQR has vertices P(x1, y1), Q(x2, y2), and R(x3, y3).
The area of ΔPQR is given by
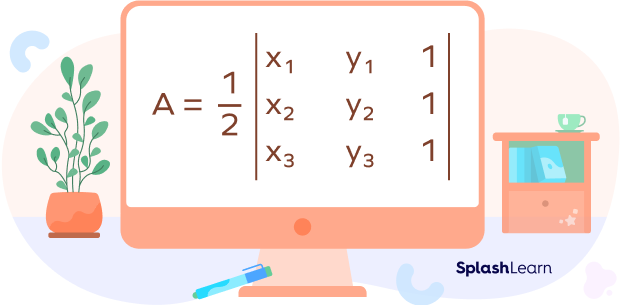
Solving the determinant, we get
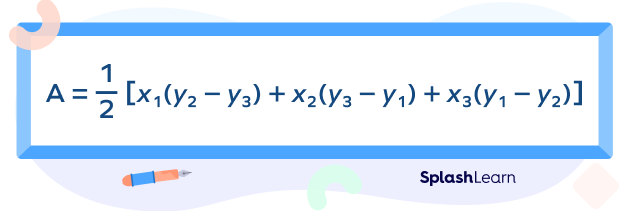
Recommended Worksheets
How to Determine the Area of Triangle in Determinant Form
Now that we know the formula to evaluate the area of triangle in determinant form, we will solve a few examples to understand its application.
A determinant value can be both positive or negative. However, area can never be negative. So, we take the absolute value of the result.
Example: Suppose the vertices are P(-1, 2), Q(3, 1), and R(2, 5). So, if we want to determine the area of triangle in determinant form, we will use the above-mentioned formula.
Area $= \frac{1}{2} \times \left[x_{1} (y_{2} – y_{3}) + x_{2} (y_{3} – y_{1}) + x_{3} (y_{1} – y_{2})\right]$
Here, we know that the coordinates of vertices are P(x1, y1), Q(x2, y2), and R(x3, y3).
x1= -1, y1= 2
x2= 3, y2= 1
x3= 2, y3= 5
Putting the values in the formula, we get
A $= (\frac{1}{2}) \left[(-1) (1 – 5) + 3 (5 – 2) + 2 (2 – 1)\right]$
A $= \frac{1}{2} \times 15$
A $= \frac{15}{2}$ square units
Facts about Area of Triangle in Determinant Form
- For three collinear points, we get a straight line and the determinant becomes zero.
- If the area of the triangle is 0, the three points are collinear.
- Area cannot be negative. Thus, if the determinant comes out to be negative, consider the positive value only.
- If the area of a triangle is given and we have to find a missing coordinate of a vertex, we consider both positive and negative values of the determinant.
Conclusion
In this article, we delved into the concept of finding the area of a triangle using the determinant form, a powerful method in linear algebra. We learned how determinants are used to find the area of a triangle, the formula and examples. To reinforce our knowledge, let’s engage in solving examples and attempting MCQs for better comprehension.
Solved Examples on Area of Triangle in Determinant Form
1. The three vertices of ▵GHI are G(–1, 1), H(3, 4), and I(2, –1). How can we find the area of this triangle?
Solution:
In a case where we just have the vertices given, we can find the area by using the determinant formula.
x1 = –1, y1 = 1
x2 = 3, y2 = 4
x3 = 2, y3 = -1
So, let us use the determinant formula.
Area $= \frac{1}{2} \times \left[x_{1} (y_{2} – y_{3}) + x_{2} (y_{3} – y_{1}) + x_{3} (y_{1} – y_{2})\right]$
Putting the values of the vertices in the formula, we get
A $= \frac{1}{2} \times \left[(-1) (4 – (-1)) + 3 (-1 – 1) + 2 (1 – 4)\right]$
A $= \frac{1}{2} \times \left[-5 – 6 – 6\right]$
A $= \frac{-17}{2}$ sq units
Therefore, the area of the triangle GHI is 3.5 sq units.
2. Use a determinant to find the area of the triangle with the given vertices: A(2, 4), B(5, 6), and C(1, 3).
Solution:
x1 = 2, y1 = 4
x2 = 5, y2 = 6
x3 = 1, y3 = 3
So, let us use the determinant formula.
Area $= \frac{1}{2} \times \left[x_{1} (y_{2} – y_{3}) + x_{2} (y_{3} – y_{1}) + x_{3} (y_{1} – y_{2})\right]$
Putting the values in the formula, we get
Area $= \frac{1}{2} \times \left[2 (6 – 3) + 5 (3 – 4) + 1 (4 -6)\right]$
Area $= \frac{1}{2} \times | -1 | $
Area = 0.5 square unit
Therefore, the area of the triangle ABC is 0.5 square unit.
3. The vertices of a triangle are given as P(0, 0), Q(2, 4), and R(5, 1). What would be the area of this triangle?
Solution:
x1= 0, y1= 0
x2= 2, y2= 4
x3= 5, y3= 1
A $= \frac{1}{2} \times \left[x_{1} (y_{2} – y_{3}) + x_{2} (y_{3} – y_{1}) + x_{3} (y_{1} – y_{2})\right]$
Putting the values of the vertices in the formula, we get
A $= (\frac{1}{2}) \times \left[0 (4 – 1) + 2 (1 – 0) + 5 (0 – 4)\right]$
A $= (\frac{1}{2}) \times |-18|$
A = 9
Practice Problems of Area of Triangle in Determinant Form
Area of Triangle in Determinant Form - Definition, Examples
Which is the correct formula for the area of a triangle using the determinant method?
If the coordinates of the vertices of a triangle are $(x_{1}, y_{1}), (x_{2}, y_{2})$, and $(x_{3}, y_{3})$, the area is given by
A $= \frac{1}{2} \times \left[x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2})\right]$.
Consider a triangle whose vertices are located at (-3, 1), (4, 3), and (-1, 5). Using the determinant method, calculate the area of this triangle.
A $= \frac{1}{2} \times \left[x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2})\right]$
A $= \frac{1}{2} \times \left[(-3) (3 - 5) + 4 (5 - 1) + (-1) (1 - 3)\right]$
A $= \frac{1}{2} \times \left[6 + 16 + 2\right]$
A $= 12 square units
Area of the triangle ABC is 0. It means that
If the area of a triangle is 0, it means that the vertices of the triangle are collinear.
Frequently Asked Questions about the Area of Triangle in Determinant Form
What is the formula for finding the area of a triangle?
Area of a triangle $= \frac{1}{2} \times$ base $\times$ height
Is it possible to calculate the area of any triangle using the determinant method?
Yes, the area of any triangle can be found by employing the determinant method if the coordinates of the vertices are known.
What is Heron’s formula for finding the area of a triangle?
Heron’s formula for finding the area of a triangle $= A = \sqrt{s(s – a)(s – b)(s – c)}$, where s is the semiperimeter of the triangle; a, b, and c are the lengths of the sides.




































