What Is the Base Area of a Cone?
The surface area of a cone’s circular base is referred to as its base area. It is simply the area of the base of a cone.
A cone is a three-dimensional geometric shape with a circular base and a curved surface that narrows down to a single point known as the apex or vertex. The base area is crucial in defining the cone’s total surface area and volume.
Before moving on to calculating the base area of a cone, it is important to recall the basics.
Parts of a Cone:
There are three parts of a cone. They are:
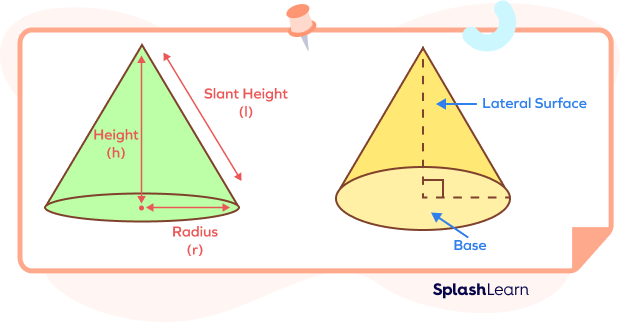
- Base: The flat circular surface at a cone’s bottom face.
- Apex (Vertex): The apex is the pointed tip of a cone where all of its slanted sides converge.
- Lateral Surface: The curved surface that joins the base with the apex.
Dimensions of a Cone:
- Height of a Cone: The vertical distance from the apex to the base.
- Slant Height of a Cone: The distance from the apex to any point on the circular edge.
- Radius of the Base of a Cone: The distance from the center of the circular base to its edge.
Recommended Games
Base Area of a Cone Formula
The formula for calculating the base area of a cone is obtained from the area of a circle. Since a cone’s base is a circle, we can calculate its base area using the method for calculating the area of a circle:
Base Area (A) $= \pi \times r^{2}$
Here
A denotes the base area of the cone
π (pi) is a mathematical constant approximately equal to 3.14159
r denotes the radius of the circular base of the cone
Recommended Worksheets
How to Find the Base Area of a Cone
Follow the steps given below to find the base area of a cone:
- Note down the radius (r) of the circular base, which is the distance from the circle’s center to any point on its edge.
- Put the values in the formula for the base area.
$A = \pi \times r^{2}$
- Simplify and assign the unit “square units” depending on the unit of the radius.
Example: If a cone has a radius of its circular base to be 5 units, then what will be the base area of the cone?
$A = \pi \times (5^{2}) = 25\pi$ square units.
Facts about the Base Area of a Cone
- The base area of a cone increases as the radius of the circular base increases.
- The cone has the largest base area among all three-dimensional shapes with a fixed volume.
- Total Surface Area of a Cone = Base Area + Curved Surface Area
- Volume of a Cone $= \frac{1}{3} \times$Base Area $\times$ Height $= \frac{1}{3}\pi r^{2}h$
Conclusion
In this article, we learned about the base area of a cone, which is represented by πr2, where r is the radius of the circular base of the cone. Understanding this fundamental concept is essential for calculating the cone’s volume and surface area. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on the Base Area of a Cone
Example 1: Calculate the base area of a 4-unit-radius cone.
Solution:
Radius (r) = 4 units
Use the formula for the base area of a cone.
$A = \pi \times r^{2}$
$A = \pi \times (4 \;units)^{2}$
$A = \pi \times 16\; units^{2}$
$A = 50.27\; units^{2}$
Therefore, the base area of the cone is 50.27 square units.
Example 2: A traffic cone has a radius of the base 7 inches. Find the base area of the cone.
Solution:
Radius (r) = 7 inches
Use the formula for the base area of a cone to find the base area of the traffic cone.
$A = \pi \times r^{2}$
On substituting the value of the radius into the formula, we get
$A = \pi (7\; inches)^{2}$
$A = \pi \times 49$ square inches
$A = 3.14 \times 49$ square inches
$A = 153.86$ square inches
Therefore, the base area of the traffic cone is 153.86 square inches.
Example 3: A cone’s circular base has to be covered with marble, and its base area is 36 square feet. What is the total cost to cover the entire base if the cost of marble is $5 per square foot?
Solution:
Total Cost = Base Area $\times$ Cost per square foot
Total Cost $= 36 \times \$5$
Total Cost $= \$180$
Example 4: Find the radius of a cone that has a base area of 100 square units.
Solution:
Base Area (A) = 100 square units
Base Area $(A) = \pi \times r^{2}$
Substitute the value of the base area in the formula, we get
$100 = \pi \times r^{2}$
Let us divide both sides of the equation by π.
$r^{2} = \frac{100}{\pi}$
Take the square root of both sides.
$r = \sqrt{\frac{100}{\pi}}$
$r = \sqrt{31.83098862}$
$r = 5.64$ units (rounded to two decimal places)
Therefore, the cone radius is about 5.64 units.
Example 5: Find the radius of the cone whose base area is 36π square meters.
Solution:
Base Area $(A) = 36\pi$ square units
On applying the formula, we get
Base Area $(A) = \pi r^{2}$
$36\pi = \pi r^{2}$
Divide both sides of the equation by π
$r^{2} = 36$
Take the square root of both sides.
$r = \sqrt{36}$
$r = 6$ units
Therefore, the radius of the cone is 6 units.
Practice Problems on the Base Area of a Cone
Base Area of a Cone - Definition, Formula, Examples, Facts, FAQs
What is the formula for computing the base area of a cone?
Base area of a cone $= \pi r^{2}$
What is the base area of a cone whose base has the radius of 10 units?
$A = \pi r^{2}$ $A = \pi \times (10)^{2} = 100\pi \;unit^{2}$
Volume of a cone =
Volume of a cone $= \frac{1}{3} \times Base \;Area \times Height$
Frequently Asked Questions about the Base Area of a Cone
What happens to the base area of a cone if the radius of the base is doubled?
When the radius of a cone’s base is doubled, the base area of the cone grows four times.
Base Area (A) $= \pi r^{2}$
Let the new radius be “2r.”
So, the new base area $= \pi \times (2r)^{2} = \pi 4r^{2} = 4(\pi \times r^{2})$
Hence, the new base area grows four times the original base area by doubling the radius.
How is the base area of a cone related to its slant height?
The base area is not directly related to the slant height; it only depends on the radius.
Is the base area the same as the lateral surface area?
No, the base area is separate from the lateral surface area of a cone. Lateral surface area is simply the curved surface area of the cone.




































