How to Convert Binary to Hexadecimal – Conversion, Steps, Examples

What Is the Binary to Hexadecimal Conversion?

The binary to hexadecimal conversion is used to convert binary numbers to the equivalent hexadecimal numbers. 

What Is a Binary Decimal System?

The binary number system is the base-2 number system. It uses only two digits, 0 and 1, to represent all the numbers. Thus, the place values of binary numbers are defined in terms of powers of 2. It is the most commonly used number system in computer systems due to its compactness. 

What Is a Hexadecimal Number System?

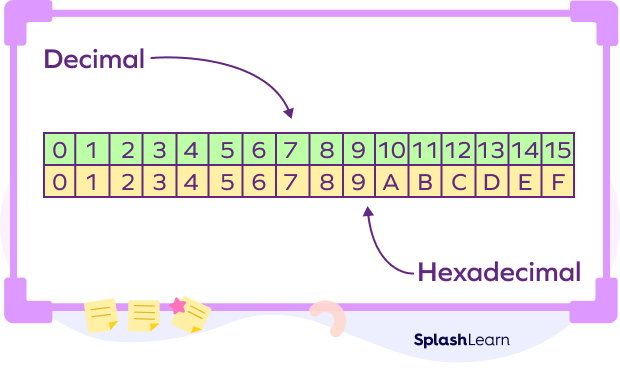
The base of the hexadecimal number system is 16. It uses 16 symbols to represent all the numbers. These symbols include 0-9 digits and A-F letters. The place values of the hexadecimal number system are defined in terms of powers of 16.

How To Convert Binary to Hexadecimal

Hexadecimal number system makes it simple to convert large binary numbers into compact hex representation. There is no direct binary to hexadecimal formula but we can use two methods for this conversion. 

Indirect Method: Binary to Decimal followed by Decimal to Hexadecimal

In this method, we first convert the binary number into its equivalent decimal number. Next, we carry out the decimal to hexadecimal conversion.

Example: Convert (1010)₂ from the binary to hexadecimal system. 

Step 1: Binary to Decimal

Find the equivalent decimal number of (1010)₂. To find the decimal equivalent, we multiply each digit with the powers of 2 starting from the ones place.

$(1010)_{2} = 1 \times 2^{3} + 0 \times 2^{2} + 1 \times 2^{1} + 0 \times 2^{0}$

(1010)₂ = 8 + 0 + 2 + 0

(1010)₂ = 10

So, (1010)₂ = (10)₁₀

Step 2: Decimal to Hexadecimal 

Convert decimal to binary by dividing the decimal number repeatedly by 16 until we get 0 quotient. Once the quotient is zero, we arrange the remainder from bottom to top (in the reverse order) to obtain the binary number.

Division	Quotient	Remainder(decimal value)	Remainder (hexadecimal value)
$10 \div 16$	0	10	A

So, (10)₁₀ = (A)₁₆

Hence, (1010)₂ = (10)₁₀ = (A)₂

Direct Method: Binary to Hexadecimal Using Grouping

We can represent a group of any 4 binary digits using a unique hexadecimal value. Simply divide the given binary number into the groups of 4. Add zeros to the left when there are not enough digits to form a group. Convert each group into the equivalent hexadecimal number using the following binary to hexadecimal table.

Binary to Hexadecimal Conversion Chart

Binary	Hexadecimal
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

This is a simple shortcut method. Before we take an example, let’s first understand how this table is created. 

Write the powers of 2 (2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8) for each digit in the group of 4 binary digits. So, we assign the numbers 1, 2, 4, and 8 starting from the leftmost digit. Add the product of the corresponding digits to find the hexadecimal number.

Powers of 2	8421	8421	8421	8421	8421	8421	8421	8421
Binary	0000	0001	0010	0011	0100	0101	0110	0111
Hexadecimal	0	1	2	3	4	5	6	7

Powers of 2	8421	8421	8421	8421	8421	8421	8421	8421
Binary	1000	1001	1010	1011	1100	1101	1110	1111
Hexadecimal	8	9	A	B	C	D	E	F

Example: Convert the binary number 10101011₂ into hexadecimal.

Let’s create groups of 4 digits starting from the ones place.

10101011₂ = 1010₂ | 1011₂

From the table, we have

1010₂ = A₁₆

1011₂ = B₁₆

Thus, 10101011₂ = (AB)₁₆

Facts about Binary to Hexadecimal Conversion

Conclusion

In this article, we learned about binary to hexadecimal conversion which is basically base-2 to base-16 conversion. We learned two methods of binary to hexadecimal conversion with steps. Let’s solve a few examples and MCQ practice problems.

Solved Examples on Binary to hexadecimal

1. Convert (00001011)₂ into a hexadecimal number system by direct method.

Solution: 

Let’s form the groups of four digits.

(00001011)₂ = (0000) | (1011)

Here, 

0000₂ = 0₁₆ 

1011₂ = B₁₆

So, (00001011)₂=(0B)₁₆ 

2. What is the value of (11110010)₂ into a hexadecimal number system?

Solution: 

Form the groups of 4.

(11110010)= (1111) | (0010)

The hexadecimal number F stands for 1111₂ and the hexadecimal number 2 stands for 0010₂.

So, (11110010)₂ = (F2)₁₆

3. Convert (1001110)₂ into a hexadecimal number system by indirect method.

Solution: 

(1001110)₂

$= 1 \times 2^{6} + 0 \times 2^{5} + 0 \times 2^{4} + 1 \times 2^{3} + 1 \times 2^{2} + 1 \times 2^{1} + 0 \times 2^{0}$

= 64 + 0 + 0 + 8 + 4 + 2 + 0

= (78)₁₀

Now, we convert (78)₁₀ into the hexadecimal number.

Division	Quotient	Remainder (Decimal value)	Remainder(Hexadecimal value)
$78 \div 16$	4	14	E
$4 \div 16$	0	4	4

Write the remainders in the reverse order.

(78)₁₀ = (4E)₁₆

4. What will you get if you convert (11011110)₂ into a hexadecimal number system?

Solution: 

Form the groups of four digits.

(11011110)₂ = 1101 | 1110

1101₂ = D₁₆

1110₂ = E₁₆

So, (11011110)₂ = (DE)₁₆

Practice Problems on Binary to Hexadecimal Conversion

Frequently Asked Questions about Binary to Hexadecimal Conversion