Circumference of the Earth: Introduction
Earth is the third planet from the sun and also the fifth-largest planet in the solar system. The term “circumference” commonly refers to the length of the boundary of a circle, but Earth is almost spherical in shape. So, what do we mean by the circumference of a sphere? Let’s find out.

What Is the Circumference of the Earth?
Although a sphere does not have a circumference, it has circular cross-sections, whose circumference can be calculated. Since the length of the radius varies as we move away from the sphere’s center, it is crucial to know which cross-section determines the circumference of the sphere. For that, you need to first determine the sphere’s great circle.
Great Circle
The largest circle that can be created around a sphere is called a great circle. Every sphere has a great circle. A great circle is a cross section of a sphere that contains a diameter of the sphere. A sphere will be split perfectly in half if you cut it at one of its great circles. A great circle has the same center point and circumference as that of a sphere.
The Earth also has many great circles. One of them is its equator. The Earth’s own radius is the radius of the great circle.
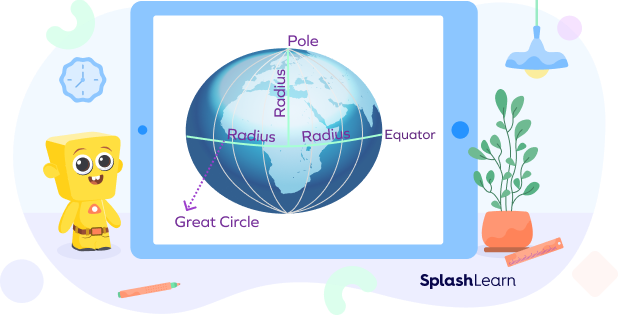
The circumference of the great circle defines the sphere’s circumference.
Mathematically, the circumference of any great circle of a sphere = 2πR or πD,
where “R” is the sphere’s radius and “D” is its diameter.
Circumference of Earth at Equator
Do you know the Sun’s tremendous gravitational pull and Earth’s rotation causes it to bulge at the equator? This makes it somewhat of a squashed sphere.

Earth, as we know now, is an oblate spheroid, as shown in the above figure. So, its circumference varies depending on how you calculate it.
At the equator, the radius of Earth is 3963 miles (Diameter = 7926 miles).
Earth’s polar radius is 3950 miles (Diameter = 7900 miles).
Circumference of the Earth in Meters
When measured around the equator, the circumference of the Earth is 40.075 million meters.
On the other hand, it is 40.008 million meters when measured from the North Pole to the South Pole.
Circumference of the Earth in Kilometers (km)
When measured around the equator, the circumference of the Earth is 40,075 km.
It is 40,008 km when measured from the North Pole to the South Pole.
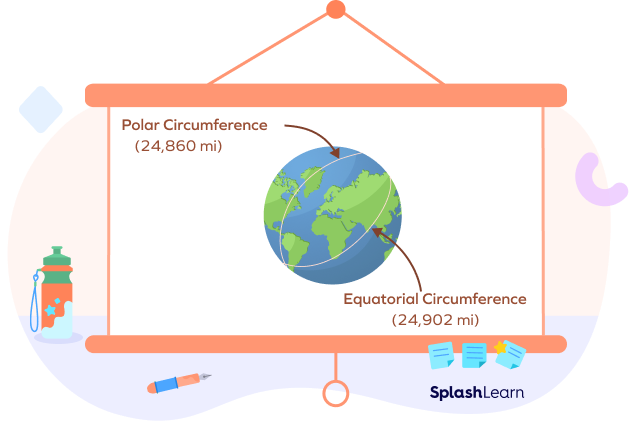
Circumference of the Earth in Miles
When measured around the equator, the circumference of the Earth is roughly 24,902 miles, whereas it is approximately 24,860 miles from the north pole to the South Pole.
Circumference of the Earth in Feet
When measured around the equator, the circumference of the Earth is 131,477,280 feet.
It is 131,260,800 feet when measured from the North Pole to the South Pole.
Method to Calculate the Earth’s Circumference
We can use a mathematical formula to find the circumference of the Earth as follows:
Circumference of Earth at the equator (CE):
CE = π × D
= 3.14 × 7926
= 24,887.64 miles (which is close to 24,901 miles)
Circumference of Earth around the poles (CP):
CP = π × D
= 3.14 × 7900
= 24,806 miles
Fun Facts
- Earth’s shape, caused by the flattening at the poles, is known as an oblate spheroid. So, its diameter at the equator is bigger than that at its polar regions.
- The average distance between the Sun and Earth is 92,935,700 miles.
- The diameter of the Sun is 109 times as great as Earth’s diameter.
- One of the ways of calculating the circumference is the geometric method employed more than 2000 years ago. It was used by Eratosthenes, the chief librarian of Alexandria in Egypt, to calculate the circumference of the Earth in 200 BCE. He arrived at the estimated figure of 28,738 miles. It is fairly close to the real value of 24,901 miles.

Conclusion
The circumference of the Earth varies depending on the length of its diameter at the equator and the poles. It is about 40,075 km around the equator and about 40,008 km from the North Pole to the South Pole.
The Greek mathematician Eratosthenes first calculated the Earth’s circumference with the help of a well, sunrays, and a stick. Now, it is calculated using the mathematical formula of 2πR or πD.
Knowing how to calculate Earth’s circumference is important because it serves as a base for understanding complex circumference problems in higher classes.
Solved Examples
1. What is the circumference of the planet Venus if its diameter is 7520.8 miles? (Take π as 3.14.)
Solution: The diameter of Venus = 7520.8 miles
Circumference (C) = π D.
Now, by substituting the value of diameter (D) in the formula, we will get
C = 3.14 × 7520.8 = 23,615.31
Therefore, the circumference of Venus = 23,615.31 miles.
2. Find the circumference of the Sun, assuming that its diameter is 865,370 miles. (Use 3.14 as the value of π.)
Solution: Diameter of the Sun = 865,370 miles
Circumference (C) = π D
Circumference of the Sun = 3.14 × 865,370 = 2,717,261.8
Therefore, the circumference of the Sun = 2,717,261.8 miles.
3. Calculate the radius of the Earth if its circumference is 24,887.64 miles. (Take π as 3.14.)
Solution: The formula for circumference (C) = πD or 2πR
Given, C = 24,887.64
2πR = 24,887.64
Therefore, the radius of Earth (R) = 24,887.642 3.14 = 3963 miles.
4. Find the circumference of a soccer ball whose great circle has a diameter of 15 inches.
Solution: The circumference (C) of the soccer ball will be:
C = πD
= 3.14 × 15
= 47.1 inches
Therefore, the circumference of the soccer ball = 47.1 inches.
5. The radius of a circular pizza is 30 inches. Find its circumference.
Solution: Circumference of a circle (C) = πD
D = 2R
By using the above formulas, we will get,
D = 2 x 30 = 60 inches
C = 3.14 x 60 = 188.4 inches
Therefore, the circumference of the pizza is 188.4 inches.
Practice Problems
What is the Circumference of the Earth? Calculation, Examples
The ratio of the circumference of Jupiter to the Earth is given as 10:1. What will be the ratio of the diameter of the Earth to Jupiter?
Circumference $= πD$
Ratio of circumferences $= πD$$\text{(Jupiter):πD(Earth)} = 10:1$
Therefore, ratio of diameters $= D$$\text{(Jupiter):D(Earth)} = 10:1$
The circumference of the Earth in miles is $\underline{}$
Earth’s circumference in miles is roughly 24,860.
At the equator, the radius of the Earth is
At the equator, the radius of Earth is 3963 miles.
The circumference of the Earth at the equator (CE) is $\underline{}$ .
The circumference of the Earth at the equator (CE) is approximately 24,901 miles.
The diameter of the bigger circle is 9 times the circumference of the smaller circle with a radius of 5 feet. Calculate the circumference of the bigger circle.
Circumference (C) $= 2π$R
C (smaller circle) $= 2 \times 5 \times π$ feet $= 10π$ feet.
D (bigger circle) $= 9 \times$ $\text{C} \text{(smaller circle)} = 9 \times 10π$ feet $= 90π$ feet.
C (bigger circle) $= 90π \times π = 90π^2$ feet.
Frequently Asked Questions
What is the meaning of pi (π)?
Pi is an irrational number that denotes the ratio of the circumference of a circle to its diameter. Along with the diameter, it helps in calculating the average circumference of the Earth.
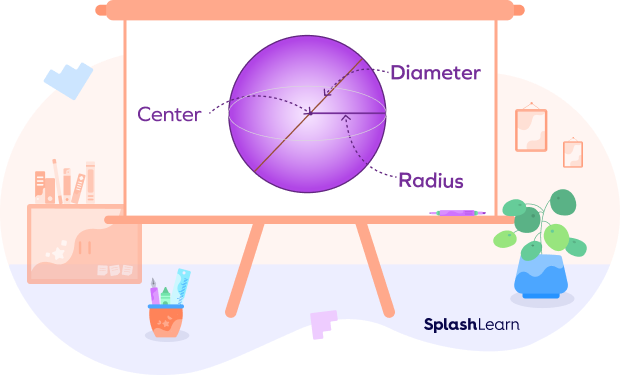
What is a diameter?
Diameter refers to a segment that passes through the center of a sphere or circle from one side to the other.
What is the meaning of a radius?
A radius refers to a straight line from the center of a sphere or a circle to its surface or circumference.
















