Clock Angle Formula – Definition, Tricks, Examples, Facts, FAQs

What Is a Clock Angle Formula?

The clock angle formula helps us determine the angle made by two hands of an analog clock at a particular time. Understanding different clock angles made by the hands of the clock is a wonderful way to relate the concept of time to the concept of angles in geometry.

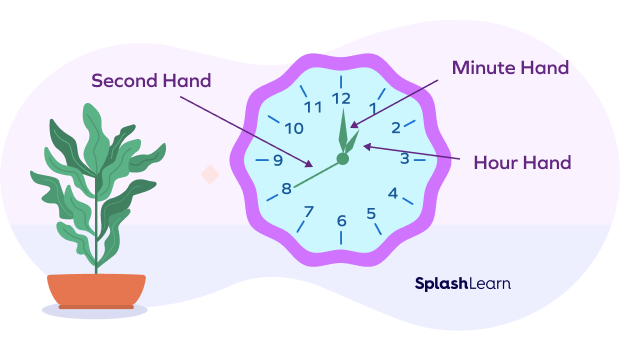
We all use analog clocks every day to tell time. The analog clock has three hands to indicate three different units of time – hour hand, minute hand, and second hand. These hands move at different speeds. A clock has a total of 12 divisions that together form a complete angle of 360. 

Clock Angle Formulas

Clock Angle Description	Formula
Angle between the minute hand and the 12 o’clock marked line:	$Angle_{mins} = 6^{\circ} \times $ Number of minutes
Angle between the hour hand and the 12 o’clock marked line:	$Angle_{hours} = (30^{\circ}$ Number of hours$) + (0.5 $\times Number of minutes$)$
One angle between the clock hands:	$=| Angle_{hours} \;-\; Angle_{minus}|$
Other angle between the clock hands:	$360^{\circ}$- First angle $= 360^{\circ}\;-\;\theta$

Clock Angle Formula Calculations

The clock angle formula is used to calculate the measure of the angle formed by the hour hand and the minute hand. 

An analog clock has 12 divisions. Between any two divisions, there is a $30^{\circ}$ angle.

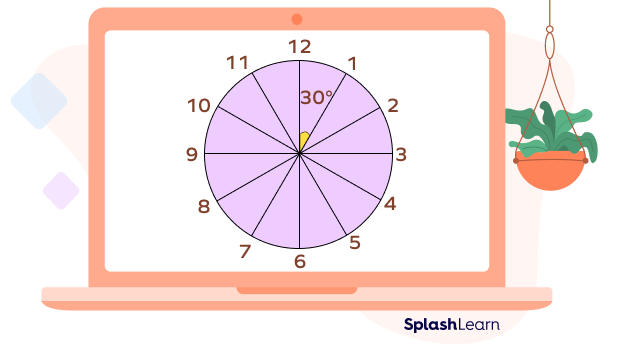
In these 12 divisions, each division is further divided into five equal parts. Each small part represents one minute and an angle of $6^{\circ}$. 

Now, it will be easy for you to understand the following table of the divisions and its angular values. Note that this is the angle made by the minute hand from the 12 o’clock mark.

Minutes	Angular Value
1 minute	$6^{\circ}$
2 minutes	$12^{\circ}$
3 minutes	$18^{\circ}$
4 minutes	$24^{\circ}$
5 minutes	$30^{\circ}$
6 minutes	$36^{\circ}$
7 minutes	$42^{\circ}$
8 minutes	$48^{\circ}$
9 minutes	$54^{\circ}$
10 minutes	$60^{\circ}$
15 minutes	$90^{\circ}$
30 minutes	$180^{\circ}$
60 minutes	$360^{\circ}$

How To Find the Angle between Hands of a Clock

Three hands move at different speeds. Thus, the clock angle depends on the hands we consider in the measurement. Suppose we wish to measure the angle made by the minute hand and the hour hand. Let’s understand how many degrees each hand produces in one minute. It will help you in the calculations.

How Many Degrees Does an Hour Hand Move In a Minute? (Bold)

The hour hand completes $30^{\circ}$ in one hour. Thus, it covers $360^{\circ}$ (a full turn) in 12 hours. It means that each hour, it moves by $30^{\circ}$.

If the hour hand moves $30^{\circ}$ in 1 hour (60 minutes), then how many degrees does it move in a minute? It is $\frac{30^{\circ}}{60} =  0.5^{\circ}.$

Each minute, the hour hand moves by half a degree.

How Many Degrees Does a Minute Hand Move in a Minute? (Bold)

We know that 60 minutes make one hour. Thus, the minute hand completes $360^{\circ}$ in 60 minutes. Therefore, in 1 minute, the minute hand covers a $6^{\circ}$ angle.

Angle Between Hands of a Clock

We will discuss two cases to find the angle made by the hands of a clock.

Case 1: A Simple Clock Problem

When there is a full hour on a clock, determining the angle between the hour hand and the minute hand is simple. The angle is equal to the number of hours multiplied by $30^{\circ}$ since the minute hand is aimed at the number 12.

Example 1: Find the angle between the hands of a clock at 3 o’clock.

At 3 o’clock, the minute hand is at 12 and the hour hand is at 3. 

It means that the hour hand has covered the period of 3 hours. In other words, it has moved by 30 three times.

Thus, the angle made by the hour hand and the minute hand will be $30^{\circ} \times 3 = 90^{\circ}$.

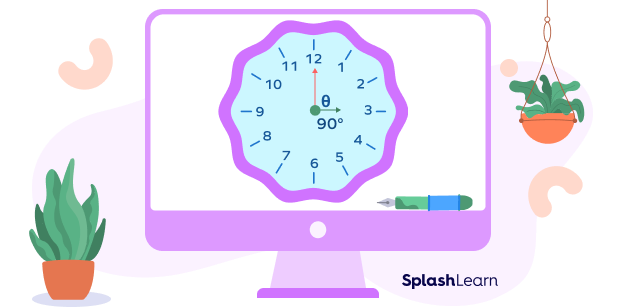
Here, we can also see that there are two angles between the hands of an analog clock. The second one is an obtuse angle, which fills the space on the other sides of an hour and minute hand. We can find it by subtracting one angle from $360^{\circ}$.

Thus, the other angle is $360^{\circ}\;-\;  90^{\circ} = 270^{\circ}$.

Example 2: Find the angle made by the hour hand and the minute hand at 04:00.

At 4 o’clock, the hour hand is at 4 and the minute hand is at 12.

Number of hours $= 4$

Angle from the minute hand to the hour hand $= 30^{\circ} \times 4 = 120^{\circ}$ 

Other angle (from hour hand to the minute hand)$ = 360^{\circ} \;-\; 120^{\circ} = 240^{\circ}$

Note that the angle is negative if we measure clockwise.

Case 2: Using a Clock Angle Formula

Let us look at the steps to find angle between hands of a clock using a clock angle formula with the help of an example.

Example: Find the angle made by the hands of a clock at 7:13.

Step 1: Draw the clock.

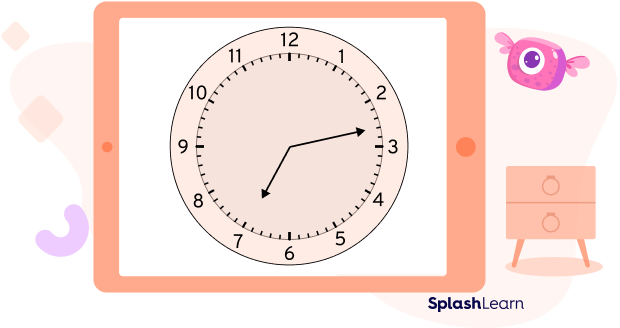
Step 2: Mark the angle between the minute hand and 12 o’clock. We know that the minute hand moves by 6° each minute. So, to calculate the angle between the minute hand and 12 o’clock, multiply the number of minutes by 6 degrees.

$Angle_{minutes} = 6^{\circ} \times$ Number of minutes

Here, the number of minutes $= 13$

$Angle_{minutes} = 6^{\circ} \times 13 = 78^{\circ}$

Step 3: Now, mark the angle between the hour hand and 12 o’clock. The hour hand moves with every minute. So, to find the correct angle, we also have to consider the number of minutes. 

Now, the hour hand moves 30° with every full hour, and then 0.5° every minute. So, the clock angle formula for the hour hand is:

$Angle_{hours} = (30^{\circ} \times$ Number of hours$) + (0.5\times$ Number of minutes$)$

In our case, the number of hours $= 7$

Number of minutes $= 13$

$Angle_{hours} = (30^{\circ} \times 7) + (0.5^{\circ} \times 13) = 210^{\circ} + 6.5^{\circ} = 216.5^{\circ}$

Step 4: Finally, find two clock angles. To find the first angle, find the absolute value of the difference of two angles:

• First angle $= |\text{Angle in hours – Angle in minutes}|$

• $\text{Second angle} = 360^{\circ} \;-\; \text{First angle}$

In our example,

• First angle between clock hands $= |216.5^{\circ} \;-\; 78^{\circ}| = 138.5^{\circ}$
• Second angle $= 360^{\circ} \;-\;  138.5^{\circ} = 221.5^{\circ}$

Facts about Clock Angle Formula

Conclusion

In this article, we have learned about the clock angle formulas, clock angle formula tricks, and methods of finding the angle by the hands of a clock. Let us solve some examples and practice problems to understand the concept better.

Solved Examples on Clock Angle Formula

1. What is the angle between the hour hand and minute hand in an analog clock at 6 o’clock?

Solution:

The angle between any two divisions is $30^{\circ}$.

The angle is equal to the hour multiplied by 30 degrees.

Angle between clock hands $= 30^{\circ} \times 6 = 180^{\circ}$

The angle between the hands of a clock at 6 o’clock is $180^{\circ}$.

2. At 5:00, what is the angle between the hour and minute hand on a clock? 

Solution: 

At 5:00, the hour hand is on the 5 and the minute hand is at the 12. 

There are 12 divisions on a clock. 

Each division represents a $30^{\circ}$ angle.

At 05:00, the hands are separated by 5 divisions.

Thus, the angle made by the hands is $30^{\circ} \times 5=150^{\circ}$.

The angle between the hour and minute hand on a clock at 5:00 is 150

3. Find the angle between the clock hands at 9:26.

Solution: 

Number of minutes $= 26$

$Angle_{mins} = 6^{\circ} \times 26 = 156^{\circ}$.

Number of hours $= 9$

$Angle_{hrs} = (30^{\circ} \times 9) + (0.5^{\circ} \times 26) = 270^{\circ} + 13^{\circ} = 283^{\circ}$.

First angle (from minute hand to hour hand) $= Angle_{hrs} \;-\; Angle_{mins} = 283^{\circ} \;-\; 156^{\circ} = 127^{\circ}$

Second angle (from hour hand to minute hand) $= 360^{\circ} \;-\;  \text{First angle} = 360^{\circ} \;-\; 127^{\circ} = 233^{\circ}$

Practice Problems on Clock Angle Formula

Frequently Asked Questions on Clock Angle Formula