Complement of a Set – Definition, Properties, Examples, Facts, FAQs

What Is the Complement of a Set?

In set theory, the complement of a set is the set of all elements that belong to the universal set but not to the original set.

The complement of a set A is denoted by A’ or Ac.

Example:

Universal set $= U =$ Set of all integers 

$U = \left\{…, -\;3,\;-\;2,\;-\;1,\; 0,\; 1,\; 2,\; 3,…\right\}$

Let A be the set of even integers.

$A = \left\{…,\;-\;2,\; 0,\; 2,\; 4,…\right\}$

Here, the complement of A is the set of odd integers.

Complement of set $A = A’ = \left\{…,\;-\;3,\; -\;1,\; 1,\; 3,…\right\}$

Definition of Complement of a Set

The difference between the universal set U and set A is called the complement of that set A.

If U is a universal set and A be any subset of U, then the complement of A is the set of all members of the universal set U, which are not the elements of A. 

Mathematically, the complement of a set A with respect to a universal set U is defined as 

$A’ = \left\{x \in U : x \in A\right\}$

The complement of A is the set of all elements x in U that are not in A.

Complement of a Set Symbol

The complement of the set A is denoted as A’ or A^c . The notation of the complement of a set uses an apostrophe (‘) or a superscript c after the name of the set. 

Also, as we know that the complement of A is the difference between Universal set and the set A, we can write

$A’ = U\;-\;A$

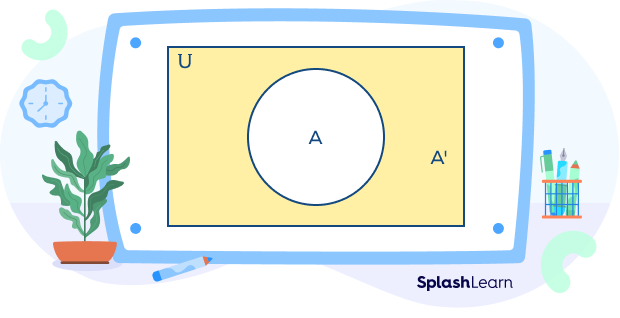
Complement of a Set: Venn Diagram

A universal set is typically represented using a rectangular box. Subsets of the universal set are generally represented by a circle. The complement of a set is the region of the universal set outside the set A.

The Venn diagram of the complement of set A is shown below. Here, the shaded portion in yellow shows the complement of set A.

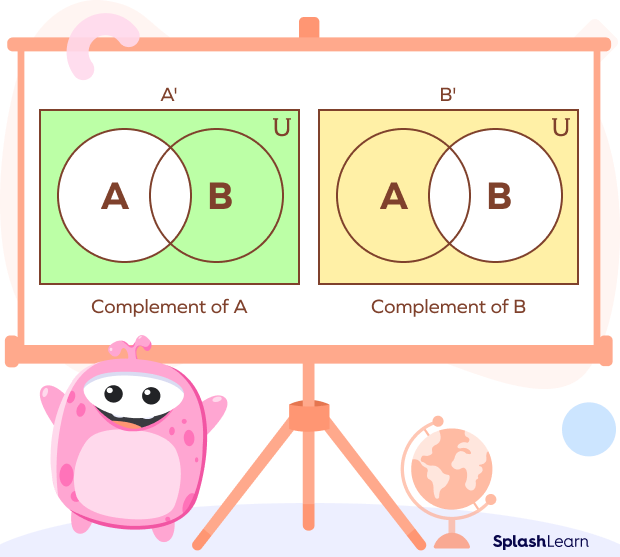
If we have two sets that intersect each other, the complements of sets can be represented as follows:

Cardinality of the Complement of a Set

Let the cardinality of the set A be n(A), the cardinality of the universal set U be n(U), then the cardinality of the complement of A, which is represented by n(A’) or |A’| is given by

$n(A’) = n(U) \;-\; n(A)$

$|A’| = |U| \;-\; |A|$

Properties of the Complement of a Set

Let’s discuss the properties of the complement of a set.

Complement Laws

• The union of a set A and its complement A’ is equal to the universal set U.

$A \cup A’ = U$

• The intersection of set A and A’ is the empty set

$A \cap A’ = ∅$

Law of Double Complementation

The complement of the complement of a set A is equal to A itself.

$(A’)’ = A$

Law of Empty Set and Universal Set

An empty set or null set (∅) is the complement of the universal set. The universal set is the complement of the empty set.

$∅’ = U$

$U’ = ∅$

De Morgan’s Laws

De Morgan’s laws are a set of two fundamental laws in a set theory that relate the complement of set operations. They are named after the mathematician Augustus De Morgan, a British mathematician .

How to Find the Complement of a Set

To find the complement of a set, follow the steps mentioned below:

Step 1: Write the elements of the universal set. Write down all the elements in the original set.

Step 2: Find the difference between U and A. In other words, identify all the elements in the Universal set that do not belong to the original set. 

Step 3: The elements identified in step 3 form the complement of the set.

Example: $U = \left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\right\}$

$A = \left\{1, 3, 5, 7, 9\right\}$

$A’ = U\;-\;A = \left\{ 2, 4, 6, 8, 10\right\}$

Facts about the Complement of a Set

Conclusion

In this article, we have discussed the complement of a set, the notation, the Venn diagram, the properties of the complement of a set, and the method to find the complement. Let’s solve a few examples and practice problems.

Solved Examples on the Complement of a Set

1. Let set $B = \left\{\text{Monday, Tuesday, Wednesday, Friday}\right\}$. Find the complement of B.

Solution: 

$B = \left\{\text{Monday, Tuesday, Wednesday, Friday}\right\}$.

Here, $U =$ Set of all days in a week

$U = \left\{\text{Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}\right\}$

Let’s find the complement of B.

$B’ = U\;-\;B$

$B’ = \left\{x | x \text{is a day of the week and x is not in B}\right\}$

$B’ = \left\{\text{Thursday, Saturday, Sunday}\right\}$.

2. Let $Y = \left\{x | x \text{is a positive even integer}\right\}$. Find the complement of Y, if U is the set of positive integers.

Solution: 

$Y = \left\{x | x \text{is a positive even integer}\right\}$

Here, U is the set of positive integers.

Therefore, $Y’ = \left\{x | x \text{is a positive integer and x is odd}\right\}$ 

$Y’ = \left\{1,\; 3,\; 5,\; 7,\; 9, …\right\}$.

3. If $U = \left\{1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8,\; 9,\; 10\right\}$ and $A = \left\{2,\; 3,\; 5,\; 7\right\}$. Find the complement of A.

Solution:

$U = \left\{1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8,\; 9,\; 10\right\}$

$A = \left\{2,\; 3,\; 5,\; 7\right\}$

$\therefore A’ = U \;-\; A = \left\{1,\; 4,\; 6,\; 8,\; 9,\; 10\right\}$

4. If $B = \left\{x: x \text{is a vowel in English alphabets}\right\}$, then find B’.

Solution:

$B = \left\{ x : x \text{is a vowel in English alphabets.}\right\}$

$B = \left\{a,\; e,\; i,\; o,\; u\right\}$

$B’ = \left\{\text{b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, y, z}\right\}$

$B’= \left\{x: x \text{is not a vowel in English alphabets.}\right\}$

$B’ = \left\{x: x \text{is a consonant in English alphabets.}\right\}$

5. Let $U = \left\{1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8,\; 9\right\}$. If $A = \left\{1,\; 2,\; 3\right\}$ and $B = \left\{4,\; 5,\; 6\right\}$ and $C = \left\{7,\; 8,\; 9\right\}$, then find (A U B U C)’.

Solution:

$A = \left\{1,\; 2,\; 3\right\}$ and $B = \left\{4,\; 5,\; 6\right\}$ and $C = \left\{7,\; 8,\; 9\right\}$

$A U B U C = \left\{1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8,\; 9\right\} = U$

$\therefore (A U B U C)’ = U’ = ∅$ 

6. If $U = {1,\; 2,\; 3,\; 4,\; 5}$ and $C = \left\{1,\; 3,\; 5\right\}$ then find (C’)’?

Solution:

$(C’)’ = C$

$U = \left\{1,\; 2,\; 3,\; 4,\; 5\right\}$ and $C = \left\{1,\; 3,\; 5\right\}$

$C’ = \left\{2,\; 4\right\}$

Again taking the complement of C’, we get

$\therefore (C’)’ = \left\{2,\; 4\right\}’ = \left\{1,\;3,\;5\right\} = C$

Practice Problems on Complement of a Set

Frequently Asked Questions about the Complement of a Set