What Is the Congruence of Triangles?
Two triangles are said to be congruent if their corresponding sides and corresponding angles are also congruent. Congruent triangles have the same shape and the same size.
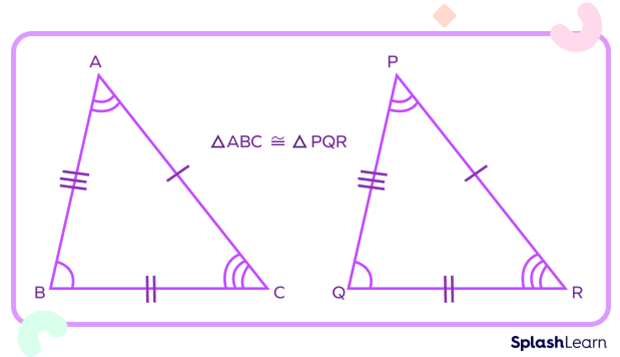
Observe the diagram shown below.
Corresponding sides: AB = DE, AC = DF, and BC = EF
Corresponding angles: ∠A = ∠D, ∠B = ∠E, and ∠C = ∠F.
Thus, two triangles are congruent.
If two figures can be placed precisely over each other, they are said to be “congruent” figures.
Recommended Games
Congruent Triangles Definition
Two triangles are said to be congruent if three sides and three angles of one triangle are congruent with the corresponding sides and angles of the other triangle.
Recommended Worksheets
Symbol of Congruence
Congruence is represented by the symbol “≅.”
Since congruence in objects implies equal shape and size; the symbol of congruence is made of two symbols, one above the other. There is a symbol of tilde “~,” which represents similarity in shape and “=” represents equality in size.
Hence, congruence is represented by the symbol as “≅.”
If two triangles are congruent to each other, we will represent it as △ABC ≅ △PQR.
How to Prove Triangles Are Congruent
A triangle has 3 sides and 3 angles. For two triangles to be congruent, all 3 sides and angles should be congruent.
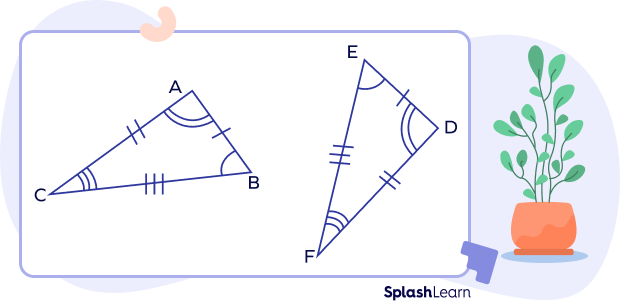
Let’s prove △ABC is congruent to △EFG.
We observe that:
AC = EG
AB = EF
BC = FG
and
∠A = ∠E,
∠B = ∠F
∠C = ∠G
Therefore, △ABC ≅ △EFG
Whenever two or more triangles are congruent, their corresponding sides and angles are also congruent by the rule of Corresponding Parts of Congruent Triangles (CPCT).
To prove the congruence of two triangles we can apply the condition of congruence, which is discussed in the next section.
Conditions of Congruence in Triangles
Two triangles are said to be congruent if their corresponding sides and angles are also congruent. We need not measure all the sides and angles of two triangles to check if they are congruent or not. There are five conditions for two triangles to be congruent, SSS, SAS, ASA, AAS, and RHS. If they follow any one of the given criteria, then they are congruent.
What Are the 5 Types of Triangle Congruence?
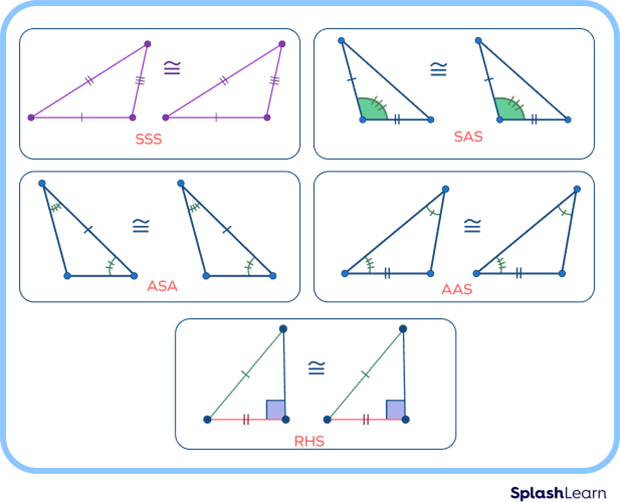
The five types of triangle congruence criteria are as follows
- SSS triangle congruence (Side-Side-Side)
- SAS triangle congruence (Side-Angle-Side)
- ASA triangle congruence (Angle-Side-Angle)
- AAS triangle congruence (Angle-Angle-Side)
- RHS triangle congruence( Right angle-Hypotenuse-Side)
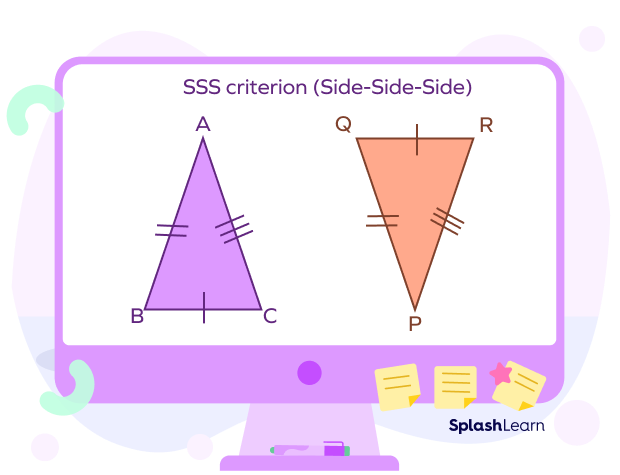
SSS Criterion for Triangle Congruence
Two triangles ABC and PQR are said to be congruent by SSS criteria if their corresponding sides are equal.
In the following image, we have
- AB = PQ
- BC = QR
- AC = PR
Thus, by SSS criterion, △ABC ≅ △PQR.
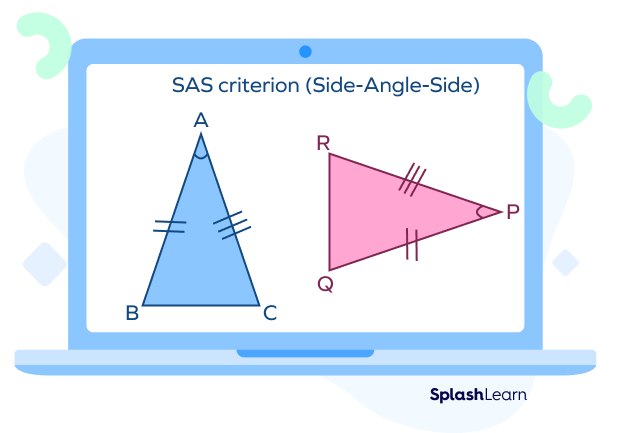
SAS Criterion for Triangle Congruence
Two triangles ABC and PQR are said to be congruent by SAS criteria if two of their corresponding sides and the angle included between them are equal.
- AB = PQ
- ∠A = ∠P
- AC = PR
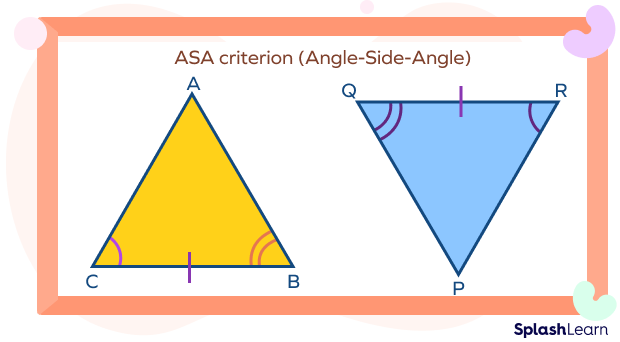
ASA Criterion for Triangle Congruence
Two triangles ABC and PQR are said to be congruent by ASA criteria if any two angles and the side included between the angles are equal.
- ∠B = ∠Q
- BC = QR
- ∠C = ∠R
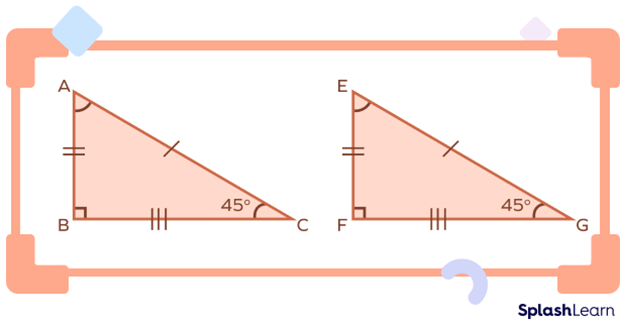
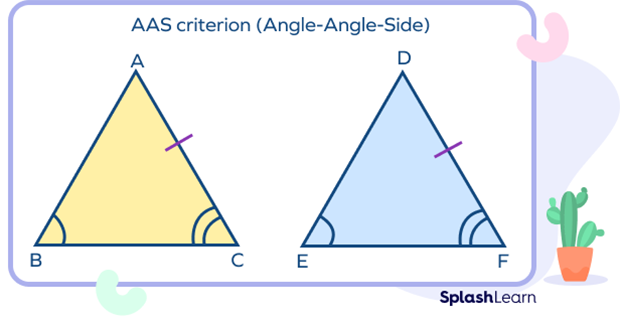
AAS Criterion for Triangle Congruence
Two triangles ABC and PQR are said to be congruent by AAS criteria if any two of their corresponding angles and any non-included side are equal.
- ∠B = ∠E
- ∠C = ∠F
- AC = DF
Thus, triangles ABC and DEF are congruent by AAS criterion.
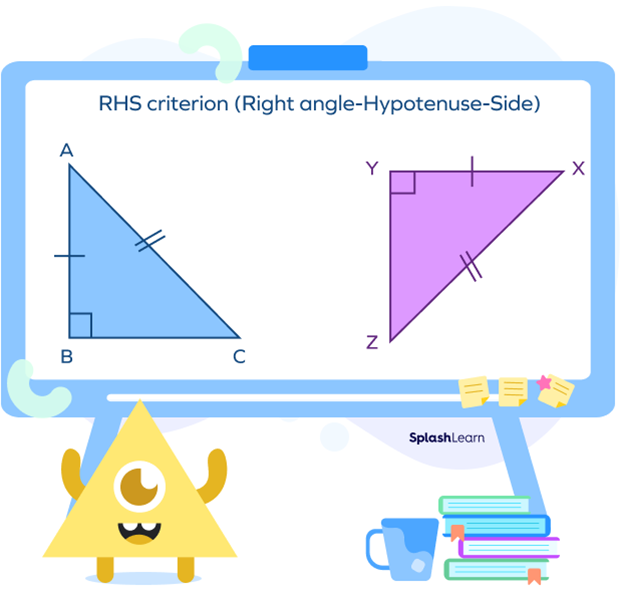
RHS or HL Criterion for Triangle Congruence
Two right triangles ABC and XYZ are said to be congruent by RHS or HL criteria if their corresponding hypotenuse and one pair of corresponding sides are equal.
- ∠B = ∠Y (right angle)
- AC = XZ (hypotenuse)
- AB = XY (side)
Congruent Triangles Examples
Here are a few examples of congruent triangles with different criteria.
CPCTC Rule
The CPCTC theorem is one of the important triangle congruence theorems. It states that when two triangles are congruent, then every corresponding part of one triangle is congruent to the other.
(CPCTC: Congruent Parts of Congruent Triangles are Congruent.)
Facts about Congruence of Triangles
- Congruent triangles can be flipped over and joined along one side to form a parallelogram or quadrilateral.
- In most bridges, congruent triangles are used to maintain a balanced weight.
- Additionally, these triangles are also used in the construction of enormous structures throughout the world.
- There is no AAA criterion since two triangles with three congruent triangles may or may not have the same shape.
- Area and perimeter of two congruent triangles are the same.
Conclusion
In this article, we have learned about congruence of triangles, types of triangles congruence, conditions of congruence, important facts about triangles congruence, frequently asked questions and examples.
Solved Examples on Congruence of Triangles
- Determine whether the triangles listed below are congruent or not, and identify the criterion test for triangle congruence.
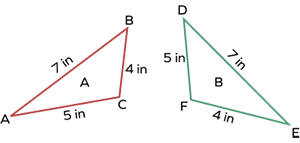
Solution:
In the above triangle, we have
AB = DE = 7 in … side
BC = EF = 4 in … side
AC = DF = 5 in … side
Hence, we can say that Δ ABC ≅ Δ DEF by the SSS congruence criteria.
- Determine whether the triangles listed below are congruent or not, and identify the criterion test for triangle congruence.
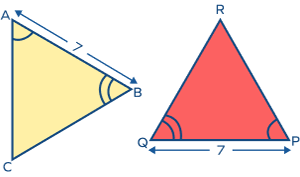
Solution:
In the above triangle, we have
∠A = ∠P … angle
AB = PQ = 7 units …included side
∠B = ∠Q … angle
Now, we can say that ΔABC ≅ ΔPQR by the ASA congruence criteria.
- Determine whether the triangles listed below are congruent or not, and identify the criterion test for triangle congruence.
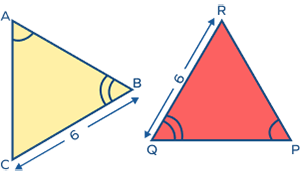
Solution:
In the above triangle, we have
∠A = ∠P
∠B = ∠Q
BC = QR = 6 units
Now, we can say that Δ ABC ≅ Δ PQR by the AAS congruence criteria.
- Two triangles MNO and XYZ are congruent. Mention the corresponding sides and angles that will be equal.
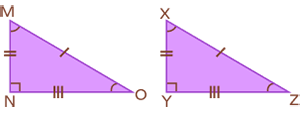
Solution:
Given, ∆MNO ≅ ∆XYZ
As per CPCTC, all the three corresponding sides and angles of congruent triangles ∆MNO and ∆XYZ will be equal to each other.
Therefore,
MN = XY, NO = YZ, and MO = XZ
Also,
∠M = ∠X, ∠N = ∠Y, and ∠O = ∠Z
- Find the length of QR and measure ∠B if ∆ABC ≅ ∆PQR and BC = 7 inches, ∠Q = 600.
Solution:
∆ABC ≅ ∆PQR
BC = 7 inches, ∠Q = 600.
ln ΔABC and ΔPQR,
By applying the CPCT (Corresponding Parts of Congruent Triangles) rule of congruence, we get
QR = BC = 7 inches
∠B = ∠Q = 600.
Hence, length of QR is 7 inches and ∠B is equal to 600.
Practice Problems on Congruence of Triangles
Congruence of Triangles: Definition, Fact, Examples, FAQs
If two figures have the same shape and size, then they are ______.
If two figures have the same shape and size then they are called congruent figures.
Which of the following is the symbol of congruence?
The symbol of congruence is $\cong$.
Which of the following is not a congruence criterion of triangles?
AAA is not a congruence criterion of triangles.
The perimeters and areas of two congruent triangles _________ equal.
Since, two congruent triangles have the same shape and size. Hence, if two triangles are congruent, then their perimeters and areas are also equal.
Two triangles XYZ and STU are said to be congruent by ASA criteria then which of the following is correct?
Given, two triangles XYZ and STU are said to be congruent by ASA criteria.
Hence, according to CPCT ∠X = ∠S, ∠Z = ∠U, and XZ = SU all are correct.
Frequently Asked Questions about Congruence of Triangles
Can two quadrilaterals be congruent ?
Yes, two quadrilaterals are congruent. Two quadrilaterals are said to be congruent if their four corresponding sides and four corresponding interior angles are equal.
What is the meaning of CPCT?
CPCT stands for “corresponding parts of congruent triangles.”
How does RHS/HL congruence work?
Two right triangles are said to be congruent by RHS criteria if their corresponding hypotenuse and one pair of corresponding sides are equal.
Does AAA congruence exist?
The AAA criterion cannot be used to demonstrate congruence in triangles. There is a chance that two triangles are similar if three of their angles are the same as those of the other triangle. For example, all three angles of two equilateral triangles are the same, but their sides could be different, so they won’t be congruent instead of having three angles that are similar. Thus, AAA congruence criterion does not exist.
What are the major differences between the similarity and congruence of the triangle?
Similar shapes can be resized versions of similar shapes, whereas congruent figures have identical lengths. This is the difference between congruence and similarity of triangles. As a result, we can say that a congruent triangle is the same as a similar triangle, whereas a similar triangle can be congruent or not.



























