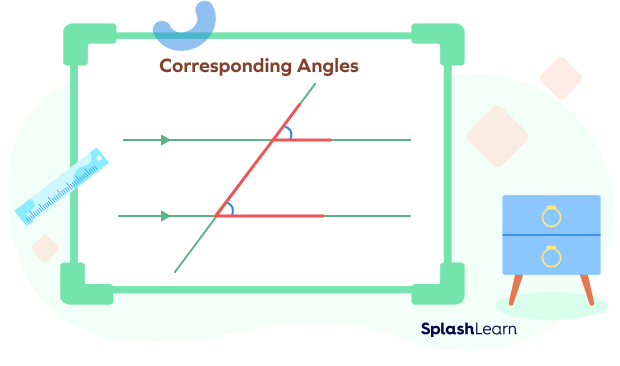
What Are Corresponding Angles?
If two parallel lines or non-parallel lines are cut by a transversal, the angles at the in matching corners or corresponding corners on the same side of the transversal are called “corresponding angles.”
So, what do the corresponding angles look like? In each pair of corresponding angles, one angle is in the interior region of the two lines and one angle is in the exterior region.
Recommended Games
Corresponding Angles: Definition
When two lines are crossed by a transversal, corresponding angles are pairs of angles that are in the same relative position in relation to a pair of intersecting lines.
Recommended Worksheets
Types of Corresponding Angles
The two cases that may arise while checking corresponding angles are as follows:
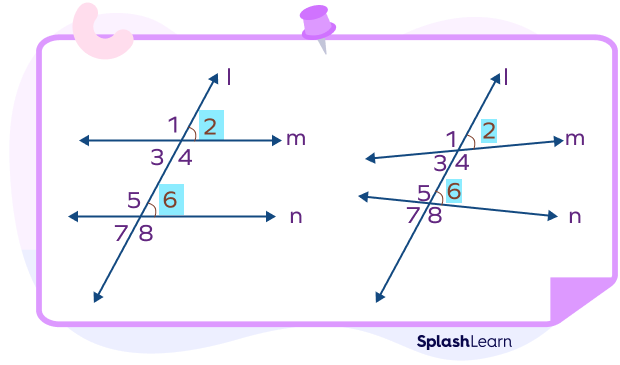
- Corresponding angles formed by parallel lines and transversals
When two or more parallel lines are cut by a transversal, then the corresponding angles are formed at the matching corners or at the same relative position at each intersection.
When the lines are parallel, each pair of corresponding angles are congruent.
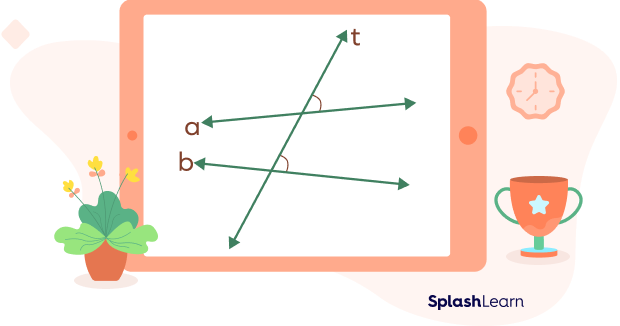
- Corresponding angles formed by non-parallel lines and transversals
In the case of non-parallel lines, the angles in previously stated positions will remain corresponding angles. However, they will not be equal in measure anymore. Two non-parallel lines form pairs of non-congruent corresponding angles.
How to Locate and Identify Corresponding Angles
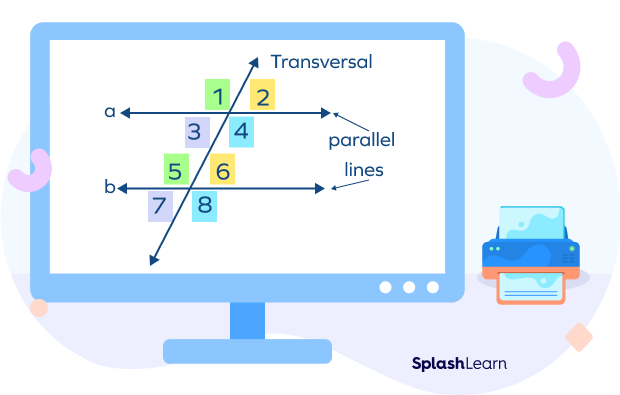
Let’s understand how to identify which angles are corresponding angles when two parallel lines (or non-parallel lines) are cut by a transversal.
- They lie on the same side of the transversal.
- They lie at the matching corners.
- In each pair, one angle is in the interior region and the other is outside the two parallel (or non-parallel) lines.
- Corresponding angles form a F-shaped pattern.
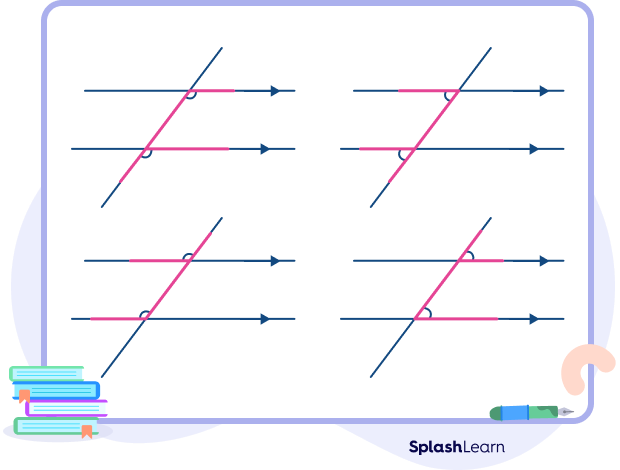
Corresponding Angles Theorem
The corresponding angle theorem states that when parallel lines are cut by a transversal, each pair of corresponding angles are congruent or equal.
Converse of Corresponding Angles Theorem
If the corresponding angles are congruent, the lines intersected by transversal are parallel.
Facts about Corresponding Angles
- If non-parallel lines are cut by a transversal, the corresponding angles are not congruent. There is no specific relationship between the corresponding angles.
- If parallel lines are cut by a transversal, the corresponding angles are congruent.
Conclusion
In this article, we learned about the corresponding angles formed by parallel lines and non-parallel lines with a transversal. Let’s solve a few examples and practice problems based on the concept of corresponding angles.
Solved Examples on Corresponding Angles
1. The measures of corresponding angles formed by two parallel lines and a transversal are (x + 20)° and (3x + 9)°. What is the value of x?
Solution:
The corresponding angles formed by parallel lines and a transversal are always equal.
Thus, they are congruent.
x + 20 = 3x + 9
3x – x = 20 – 9
2x = 11
x = 112
x = 5.5
2. If EG and BD are two parallel lines, find the measure of the angle x.
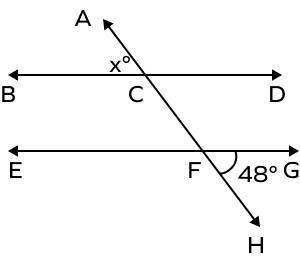
Solution: The angles ∠GFH and ∠EFC are vertically opposite angles.
Vertical angles are always congruent.
Thus, m∠CFE = m∠GFH = 48°
Now, the angles ∠EFC and ∠BCA are corresponding angles formed by parallel lines.
Thus, they will also be equal.
Thus, m∠EFC and m∠BCA = 48°.
3. Write all the pairs of corresponding angles.
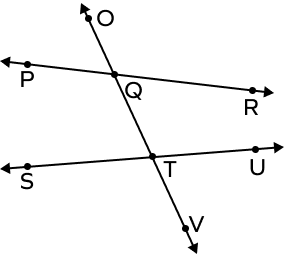
Solution:
Pairs of Corresponding Angles:
- ∠OQR and ∠QTU
- ∠RQT and ∠UTV
- ∠OQP and ∠QTS
- ∠PQT and ∠STV
Practice Problems on Corresponding Angles
Corresponding Angles - Definition, Theorem, Types, Examples
If the corresponding angles are not congruent, then
If the corresponding angles are not congruent, then the lines are not parallel.
Corresponding angles are equal, when ______ lines are cut by a transversal.
Corresponding angles will be equal if the lines cut by a transversal are parallel.
What is the corresponding angle of ∠AGE?
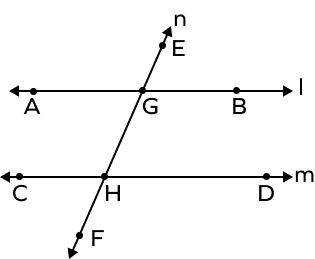
The corresponding angle of ∠AGE is ∠CHG.
Frequently Asked Questions about Corresponding Angles
Are corresponding angles equal?
Corresponding angles formed when parallel lines are cut by a transversal are equal.
What are the relative positions of corresponding angles and a transversal?
Corresponding angles are formed on the same side of the transversal, at the matching corners.
Are corresponding angles supplementary?
No, corresponding angles need not be supplementary.
What is a transversal?
Transversal is the line intersecting two lines (parallel or non-parallel) at two distinct points.





























