In mathematics, a relationship between two expressions or values that are not equal to each other is called ‘inequality.’ So, a lack of balance results in inequality. For example, if you want to buy a new bicycle that costs $250, but you have $225. It is also an inequality as you are comparing two numbers that aren’t equal.
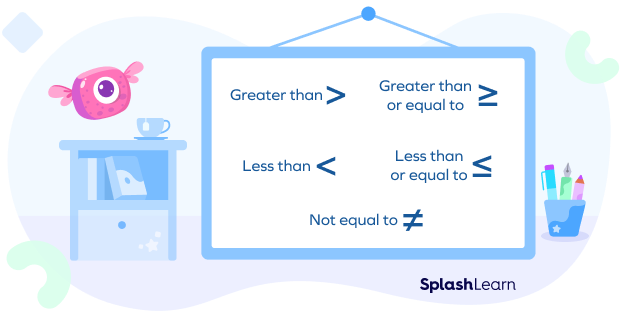
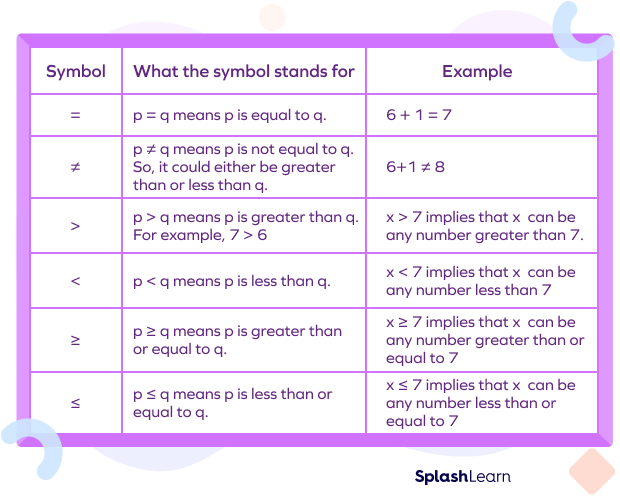
We use ‘=’ when two quantities are equal and when they are not equal we use the symbol ≠ to denote not equal. If two things are not equal, the first value can be either greater than (>) or lesser than (<) or greater than equal to (≥) or less than equal to (≤) the second value. So, as per the above example, $250 > $225.
In Mathematics,

Origin of the Term: Inequality
The term ‘inequality’ comes from the Old French word inequalité and the Latin word inequalitas, meaning ‘unequal, unlike, different’ and changeable. This term is used to compare the magnitude, number, and intensity of two values or expressions.
Recommended Games
Let’s Look at the Rules of Inequalities

Rule 1: When inequalities are linked, you can jump across them. So, if a is greater than b, and b is greater than c, a will also be greater than c.
If a > b > c, a > c, we can jump over b to find out the relation between a and c directly.
Example: If you (5) have more pens than Mia (3), and Mia (3) has more pens than Benj (1), then you (5) automatically have more pens than Benj (1).
Rule 2: If you exchange the values, the sign also reverses.
- If p > q, then q < p
- If p < q, then q > p
Example: If Mia is taller than Ben, then Ben will be shorter than Mia.
Rule 3: An inequality can either be > or < but never both at the same time.
- If x > y, then it is impossible to have an equation x < y at the same time
- If x < y, then it is impossible to have an equation x > y at the same time
Either x will be greater than y or less than y but not both.
Example: If Weight of Ball 1 > Weight of a Ball 2, then it is not possible that Weight of Ball 1 < Weight of Ball 2 at the same time.
Rule 4: Multiplying both sides of the inequality by a negative sign, reverses the sign.
- If p > q, then −p < −q
- If p < q, then −p > −q
Example: 3 > 2, but −3 < −2 in mathematics.
Rule 5: Taking a reciprocal also changes the direction of the inequality.
- If p > q, then $\frac{1}{p}$ < $\frac{1}{q}$
- If p < q, then $\frac{1}{p}$ > $\frac{1}{q}$
Example: 5 > 3 but, $\frac{1}{5}$ < $\frac{1}{3}$ in mathematics.
Rule 6: Adding or subtracting the same quantity to each side of the inequality, does not change the inequality sign.
- If p > q, then p + r > q + r
- If p < q, then p – r < q – r
Rule 7: Dividing or multiplying by a positive quantity on each side of the inequality, does not change the inequality sign.
- If p > q, then pr > qr
- If p < q, then pr < qr
Example: 5 > 3 but, $\frac{1}{5}$ < $\frac{1}{3}$ in mathematics.
Rule 8: Dividing by a negative quantity on each side of the inequality, reverses the sign.
- If p > q, then $\frac{p}{-r}$ < $\frac{q}{-r}$
- If p < q, then $\frac{p}{-r}$ > $\frac{q}{-r}$
These rules of inequalities help us find the solutions of the inequalities.
Graphical representation of inequalities
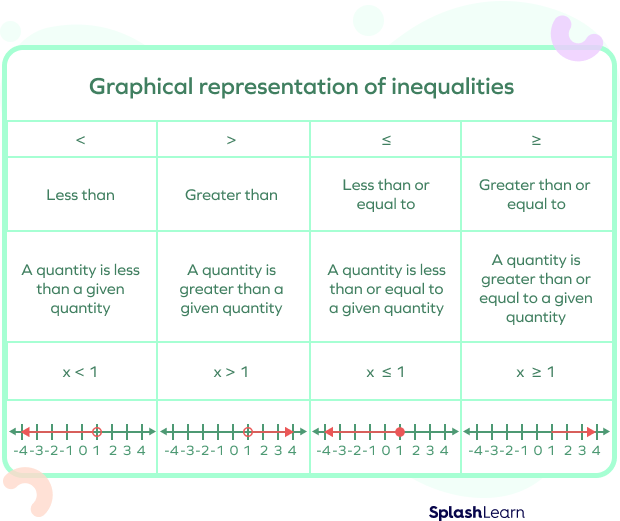
We use an empty circle to show that the limit value is not the solution to the given inequality.
Filled circle is used to show that the limit value is the solution of the given inequality.
Extending an arrow to the right end (if greater than) or left (if less than) signifies all the values the variable can take.
Recommended Worksheets
Real life Example of Inequality
- Speed limit on the road is 30 mph which can be expressed by the inequality:
Speed ≤ 30 mph
- Maximum capacity of a container is 5 liters.
Volume ≤ 5 l
- Children should not be less than 4 feet to ride the roller coaster.
Child’s height > 4 feet
- Plane has to fly at 500 m above sea level or higher.
Plane flying level $\ge$500 m
- Credit card limit per month is $5,000.
Money that can be spent in month ≤ $5,000
Solved Examples
- Given the conditions X > 30 and Y > X; which is the largest quantity?
Solution:
Y is the largest quantity as Y > X > 30.
- Determine the relation of $\frac{1}{x}$ and $\frac{1}{y}$ if x > y.
Solution:
Since signs change in reciprocals, the equation will be $\frac{1}{x}$ < $\frac{1}{y}$.
- Determine the relation of −a and −b if a < b.
Multiplying by a negative number (-1 in this case) reverses the sign.
So, −a > −b
Practice Problems
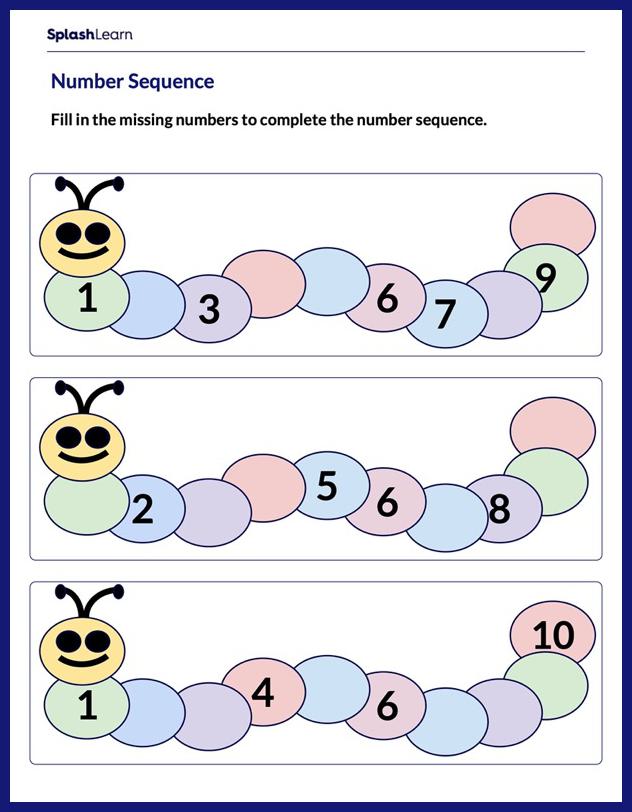
Inequality
Which of the following value satisfy the inequality?
5 - x = 5 − 2 = 3 3 ≥ 3
Identify the correct solution set for the inequality: ‘x is greater than or equal to 15.
Given inequality is x ≥ 15. So all the numbers should be either greater than or equal to 15.
Determine the correct inequality symbol between the given expressions:
(5 + 3) and (1 + 8)
Here, first we have to solve both the expressions.
5 + 3 = 8
1 + 8 = 9
Now, we know that 8 $\lt$ 9. So, (5 + 3) $\lt$ (1 + 8).
Choose the correct graph that best describes numbers greater than 0.




The number is greater than 0. x > 0 so, 0 is the limit value and it is not the solution of given inequality hence an open circle. The variable can take any value greater than 0 so we extend an arrow to the right.

Frequently Asked Questions
Can we add and subtract in the inequality?
Inequalities are very much like equations. If you want to add or subtract from one side of the equation, you must perform the same operation to the other side of the equation.
Does inequality sign remain the same always?
No, the inequality sign is reversed when we multiply or divide each side with a negative number. The sign is also reversed when we exchange the values (If p > q, then q < p) or take reciprocal (If p > q, then $\frac{1}{p}$ < $\frac{1}{q}$).
How many solutions does an inequality have?
Inequalities have infinite solutions. for example x < 5 will have all numbers less than 5 as solutions.
How are inequalities different from equations?
Equations and inequalities are both mathematical sentences formed by relating two expressions to each other. In an equation, the two expressions are deemed equal which is shown by the symbol =. Where as in an inequality we compare the relative size of values, the two expressions are not necessarily equal which is indicated by the symbols: >, <, ≤ or ≥.
Let’s do it!
Learning inequality in math is important as it is a fundamental concept that takes a larger shape in higher classes. To make more mathematical concepts easier and fun for your kids, head over to SplashLearn and sign up for free!