Definition
Equivalent decimals are decimal numbers that have the same value. These decimals are obtained by inserting zeros after the extreme right digit in the decimal part of a decimal number.
Let us look at an example:
0.3 and 0.30
They both seem different, but guess what! They are equivalent decimal numbers.
Let us understand it through an image.
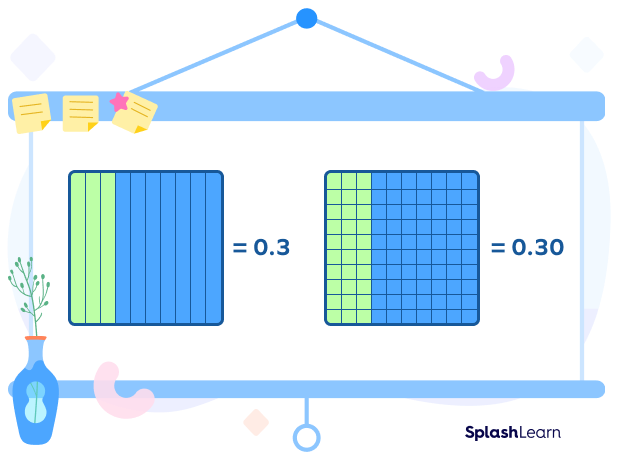
Model 1 shows 0.3 = $\frac{3}{10}$
Model 2 shows 0.30 = $\frac{30}{100}$ = $\frac{3}{10}$
In models 1 and 2, three tenths and thirty hundredths are covering the same amount of space.
The value of the decimal number remains the same whenever we add zero to the right of a decimal. The zero that we add here is called the trailing zero and it does not change the value of the decimal.
For example, 0.7 = 0.70 = 0.700
But the case is different when we place zeroes before the end of decimal. It does change the value of the number.
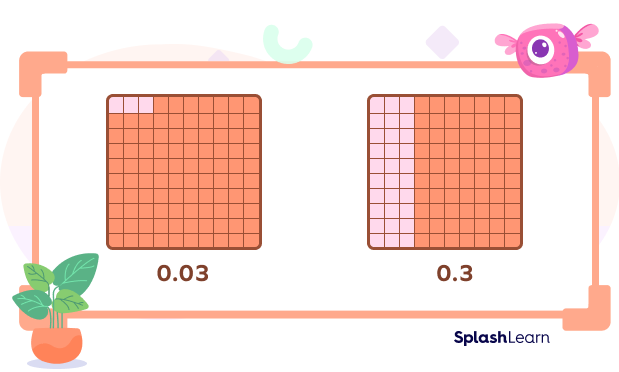
For example, 0.3 and 0.03 are non-equivalent decimals.
0.3 means $\frac{3}{10}$ whereas 0.03 means $\frac{3}{100}$.
Three tenths and three hundredths do not take up the same amount of space.
Below given are the two important concepts to understand equivalent decimals:
- We should know the difference between 0.3, 0.30, and 0.300. The place value shows that the parts of a whole get smaller from tenths, hundredths to thousandths. The reason is that each position is 10 times less as we move to the right of the decimal point.
- We should also know that 0.30 and 0.300 can both be simplified to 0.3. The additional zeros to the right of 0.3 are called placeholders.
Recommended Games
History
Decimal fractions were first developed and used by the Chinese in the end of 4th century BCE, and then spread to the Middle East and from there to Europe.
Recommended Worksheets
Rules to Identify Equivalent Decimals
- Checking the place value of the digits of the decimal numbers.
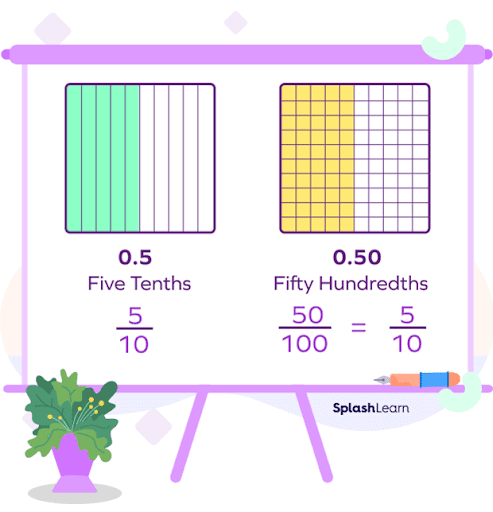
Both the numbers have the same digit (0) in the ones place. So, we will move to the right and check the digits of tenth places in both numbers. The digits in the tenth place digits (5) are also the same. If we move to the hundredth place, we observe in the first number, 0.5, there are no more digits, but in 0.50, there is a digit 0.
Hence, 0.5 and 0.50 are equivalent decimals.
- Converting the decimal numbers into the fraction.
Let us take an example
Converting 0.3 into fraction, we have $\frac{3}{10}$.
Now, converting 0.30 into fraction, we have $\frac{30}{100}$ = $\frac{3}{10}$.
Hence, 0.3 and 0.30 are equivalent decimals.
How can you make equivalent decimals?
We can make equivalent decimals by placing zeros at the end of the decimal.
0.4 = 0.40 = 0.400 = 0.4000
Equivalent Decimals vs Like Decimals
| Like Decimals | Equivalent Decimals |
| The decimals with the same number of decimal places are called like decimals. | Equivalent decimals are decimal numbers that have the same value. |
| For example, 3.42, 6.05 are like decimals as they have two decimal places. | For example, 0.3 and 0.30 are equivalent decimals as they present the same value. |
Solved Examples
Example 1: Write three equivalent decimal numbers of 2.4.
Solution: We know that the equivalent decimals have the same value. We can form them by adding zeros at the end of decimal numbers.
Therefore, 2.40, 2.400, 2.4000 are equivalent.
Example 2: Are 0.20 and 0.200 equivalent?
Solution:
0.20 = $\frac{20}{100}$ = $\frac{2}{10}$ and 0.200 = $\frac{200}{1000}$ = $\frac{2}{10}$. Thus, 0.20 and 0.200 equivalent.
Example 2: Write two non-equivalent decimal numbers of 1.65.
Solution: We can form non-equivalent decimals of the given by adding zeros before 65 in 1.65.
Therefore, two non-equivalent decimals are 1.0650, 1.0065.
Practice Problems
Equivalent Decimals - Definition With Examples
The equivalent decimal to 0.40 is?
We can form equivalent decimals of the given by adding zeros at the end of decimal numbers.
So, the equivalent decimal of 0.4 is 0.400.
Which of the following are equivalent decimals?
We can form equivalent decimals by adding zeros at the end of decimal numbers.
So, the equivalent decimal of 0.2 is 0.20.
Which of the following are non-equivalent decimals?
In option c, the zeros are to the left of 65, which will change the value.
So, 0.65 is not equivalent to 0.0065.
Frequently Asked Questions
How do you find equivalent decimals?
We can find equivalent decimals by adding zero/zeros at the end or the right side of a decimal number.
Are equivalent fractions and equivalent decimals the same?
No, the equivalent fractions and the equivalent decimals are not the same.
To find a fraction equivalent to a given fraction, we multiply/divide the numerator and the denominator of the given by the common, same non-zero number.
To find the equivalent decimals, we need to add zero/zeros at the end of the decimal numbers.
How do we verify whether a decimal number is equivalent to another decimal number?
Generally, we can verify whether a decimal number is equivalent to another by using two methods:
a. Checking the place value of the digits of the decimal numbers.
b. Converting the decimal numbers into fractions.
| Fun Facts – Decimal fractions were first developed and used by the Chinese in the end of 4th century BC, and then spread to the Middle East and from there to Europe. |
 Let’s do it!
Let’s do it!
Instead of teaching equivalent decimals and then handing out practice worksheets to your children, ask them to find the equivalent decimals of the numbers you say or convert the fractions you say into equivalent decimals.




































 Related Math Vocabulary
Related Math Vocabulary