Degrees to Radians: Conversion, Steps, Formula, Examples, Facts

What Is the Degrees to Radians Conversion?

Any angle in degrees can be converted into radians using the degrees to radians conversion. The relationship between degrees and radians is given as $2\pi = 360^{\circ}$ or $\pi = 180^{\circ}$. One complete counterclockwise revolution is represented by $2π$ (in radians) or $360^{\circ}$ (in degrees).

Degree and radian are the units for measuring an angle. An angle is a geometric figure formed when two rays meet at a common point, called vertex. When the angle is measured counterclockwise, it is called a positive angle. Angle measured in a clockwise direction is called a negative angle. 

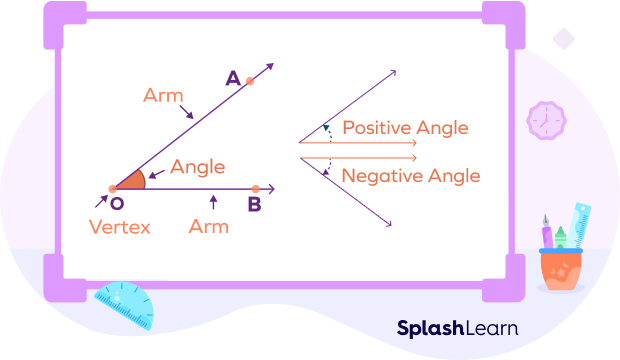
What Are Degrees?

A degree (°) is a unit for measuring the magnitude of an angle. It is the SI unit to measure angles. 

The measure of an angle in degrees is determined by the amount of rotation from the initial side to the terminal side. One complete counterclockwise rotation is $360^{\circ}$. If it is divided into 360 equal parts, each part equals one degree. Thus, 1 degree equals $\frac{1}{360}$ of a complete revolution in magnitude. 

$180° = \pi$ radians

$360=  2\pi$ radians

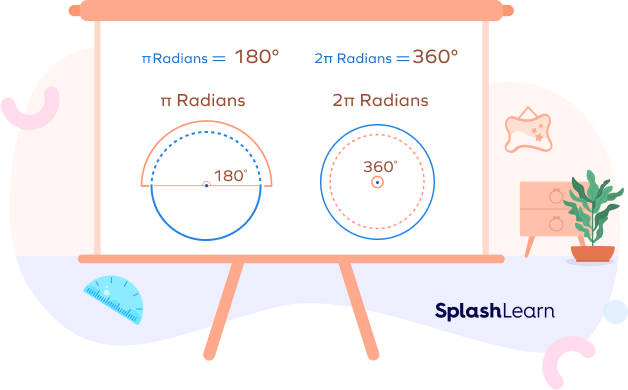
What Are Radians?

Radian is an SI unit used to measure angles. Radian is sometimes denoted by a “c” in the exponent, or by writing rad in the front of the measurement. For example, 2 radian is written as $2^{c}$ or 2 rad. Note that this symbol is often omitted in mathematical expressions.

One radian is the angle where the arc length equals the radius. The formula for angle in radians is

$\theta = \frac{Arc\;length}{Radius}$

For example, consider a unit circle (circle with radius 1 unit). An angle subtended at the center by an arc with a length of 1 unit has the measure of 1 radian. 

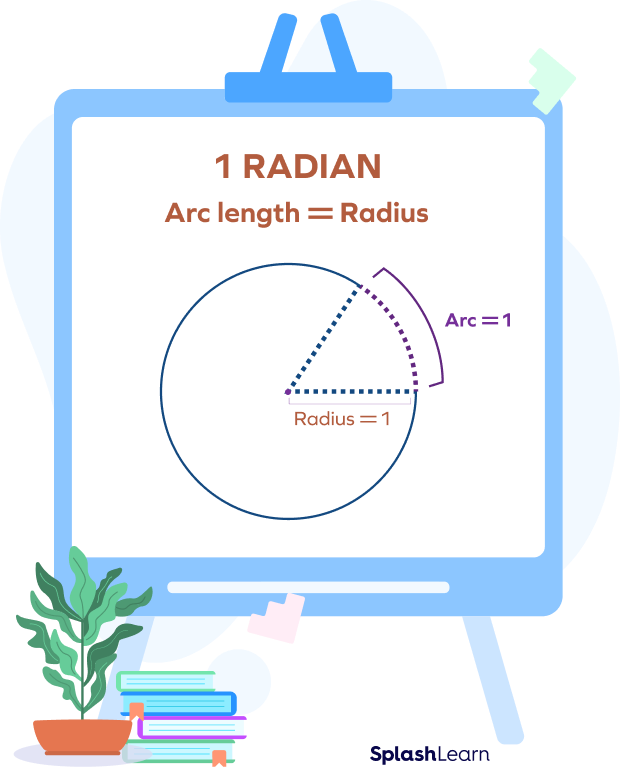
Note that all circles are similar. Thus, the measure of an angle in radians is the same regardless of the size of the circle. So, for any circle, if radius = arc length, the angle is 1 radian. One radian is approximately equal to 57.296 degrees. 

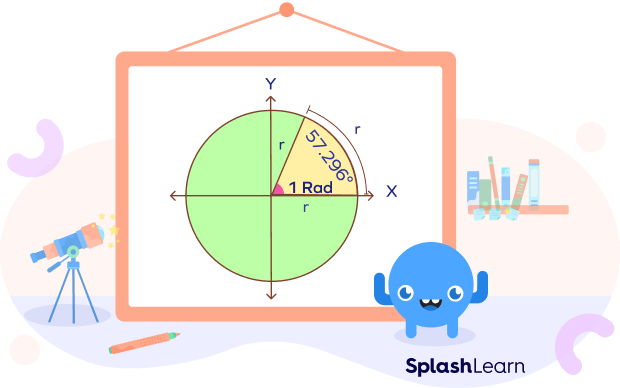
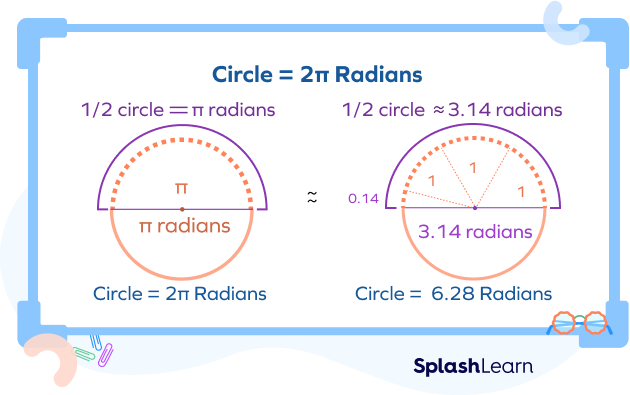
When we are dividing a circle in radians, about 3.14 radians will fit in each half of the circle. So, 6.28 radians will fit in a full circle. The exact amount of radians that fit in half a circle is π, which is about 3.14 radians. So, a full circle fits 2π radians (which is about 6.28 radians).

Degrees to Radians Formula

To convert angle in degrees to radians in terms of , we have to multiply the angle in degrees by $\frac{\pi}{180^{\circ}}$.

Angle in Radians $=$ Angle in Degrees $\times \frac{\pi}{180^{\circ}}$

Derivation of Degrees to Radians Formula

• One complete counterclockwise revolution in degrees $= 360^{\circ}$
• One complete counterclockwise revolution in radians $= 2\pi$

The relationship between degree measure and radian measure can be given as

$360^{\circ} = 2\pi$

Hence, $180^{\circ} = \pi$ radians.

$1^{\circ} = \frac{\pi}{180^{\circ}}$ Radians

Thus, to convert degrees to radians, the formula is

Angle in Radians $=$ Angle in Degrees $\times \frac{\pi}{180^{\circ}}$

To find the value of $1^{\circ}$, use the approximate value to be 3.14.

How to Convert Degree Measure to Radian Measure

We know that, 180°= radians. So, how to change degrees to radians? In order to convert any angle from the degree measure to radians, the value in degrees must simply be multiplied by $\frac{\pi}{180^{\circ}}$.

Angle in Radian $=$ Angle in Degrees $\times \frac{\pi}{180^{\circ}}$

Let’s take a look at a few examples. Convert the given angle measures from degrees to radians in terms of pi.

• $45^{\circ} = 45^{\circ} \times \frac{\pi}{180^{\circ}} =  \frac{\pi}{4}$ radians
• $90^{\circ} = 90^{\circ} \times \frac{\pi}{180^{\circ}} =  \frac{\pi}{2}$ radians

Degrees to Radians Chart

The degrees to radians chart helps us understand the conversions better.

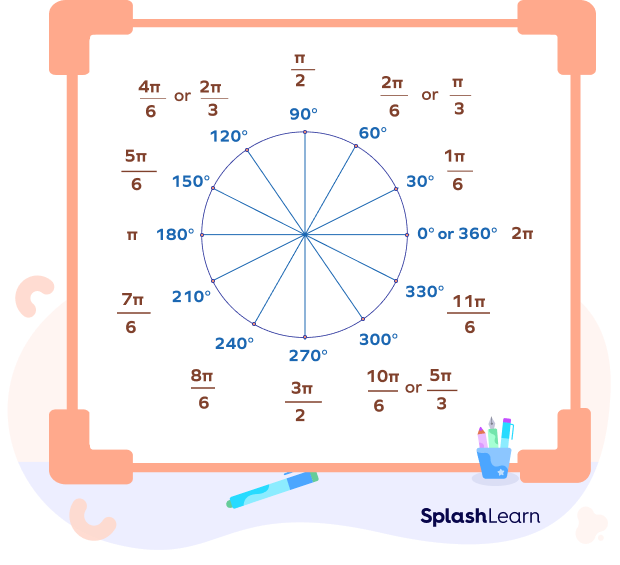
In the chart given above, values of angles are given in degrees as well as the radians that helps to do the calculations faster and easier.

Degrees to Radians Conversion Table

Let’s look at the table with some standard angles in degrees and the corresponding angles in radians.

Degrees	Radians
$30^{\circ}$	$\frac{\pi}{6}$
$45^{\circ}$	$\frac{\pi}{4}$
$60^{\circ}$	$\frac{\pi}{3}$
$90^{\circ}$	$\frac{\pi}{2}$
$180^{\circ}$	$\pi$
$270^{\circ}$	$$\frac{\pi3}{2}$
$360^{\circ}$	$2\pi$

Negative Degree to Radians

An angle measured in a clockwise direction is called a negative angle. The method for converting negative degrees to radians is the same as for positive degrees. We simply have to multiply the value of the angle in degrees by $\frac{\pi}{180^{\circ}}$.

Example: If you need to convert $(\;-\;180^{\circ})$ degrees to radian:

Angle in radians $= (\frac{\pi}{180^{\circ}}) \times (\text{Angle in degrees})$

Angle in radian $= (\frac{\pi}{180^{\circ}}) \times (\;-\;180^{\circ})$

Angle in radians $= \;-\;\pi$

Facts about Degrees to Radians

Conclusion

In this article, we learned about the units, degrees and radians and their interconversions. Let’s solve some examples for better understanding.

Solved Examples on Degrees to Radians

1. Convert each degree measure into radians.

a) $120^{\circ}$

b) $150^{\circ}$

Solution: 

Angle in Radians $=$ Angle in Degrees $ \times \frac{\pi}{180^{\circ}}$

a) $120^{\circ}$ angle in radians $=  120^{\circ} \times\frac{\pi}{180^{\circ}} = \frac{2\pi}{3}$ 

b) $150^{\circ}$ angle in radians $= 150^{\circ} \times\frac{\pi}{180^{\circ}} = \frac{5\pi}{6}$

2. Convert $\frac{2\pi}{6}$ radians to degrees.

Solution: 

Angle in degrees $=$ Angle in Radians $ \times \frac{180^{\circ}{\pi}$

Angle in degrees $=  \frac{2\pi}{6} \times \frac{180^{\circ}{\pi}  = 60^{\circ}$

3. Convert $-\;100^{\circ}$ to radians.

Solution: 

Angle in radians $= (\frac{\pi}{180^{\circ}}) \times$ (angle in degrees)

Angle in radians $= \frac{\pi}{180^{\circ}} \times (-\;100^{\circ})$

Angle in radians $= \;-\;\frac{5\pi}{9}$ radians.

4. Convert $540^{\circ}$ to radians.

Solution:

Angle in Radians $=$ Angle in Degrees $\times \frac{\pi}{180^{\circ}}$

Angle in radians $= 540^{\circ} \times \frac{\pi}{180^{\circ}} = 3\pi$ rad

Thus,  $540^{\circ} =  9.425$ radians

Practice Problems on Degrees to Radians

Frequently Asked Questions about Degrees to Radians