When they first learn how to divide numbers in school, most people are taught the traditional method of finding a common denominator and then doing long division.
However, there’s an alternative that can make the problem of dividing fractions or other numbers much easier. It’s called the area model method. Let’s learn more about it!
What is the Area Model Division?
The area of a shape is the space occupied by the shape.
If a rectangle has a length equal to 32 units and a width equal to 23 units, then we can find its area by calculating the product $32 \times 23$.
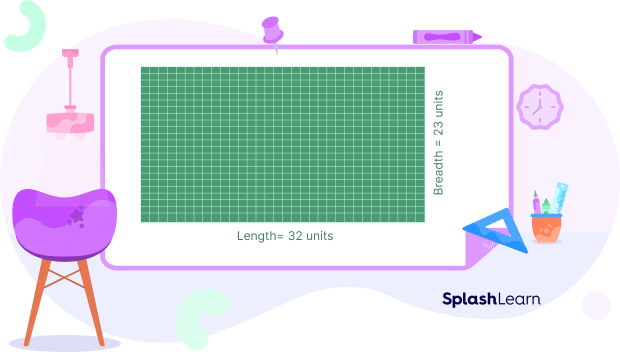
In other words, when we consider the product $32 \times 23$ geometrically, it can be interpreted as the area of a rectangle of length 32 units and width 23 units.
Similarly, we can geometrically interpret a division problem, say $555 \div 15$, as the missing dimension of a rectangle of area 555 square units and one side length 15 units.

- We can divide this rectangle into several small rectangles. Then, we can calculate the length of each small rectangle and add them together to find the length of the large rectangle.
- First, consider a small rectangle of width 15 units and length 20 units. The area of this rectangle is 300 square units. So the area of the rest of the rectangle is $555$ $–$ $300 = 255$ square units.
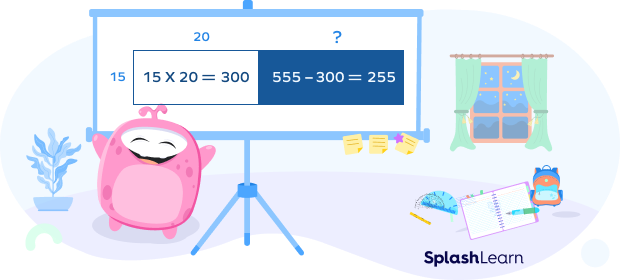
Now, we have an area of 255 square units left. Since $15 \times 10 = 150$, another rectangle of width 15 units and length 10 units can be created.

We are now left with an area of $255$ $–$ $150 = 105$ square units. As $15 \times 7 = 105$, the shaded rectangle has a width of 15 units and a length of 7 units.
Thus, the length of the large rectangle is $20 + 10 + 7 = 37$ units. Therefore, $555 \div 15 = 37$.
Recommended Games
Introducing Area Model Division
Let’s learn how to use area model division to divide 825 by 5.
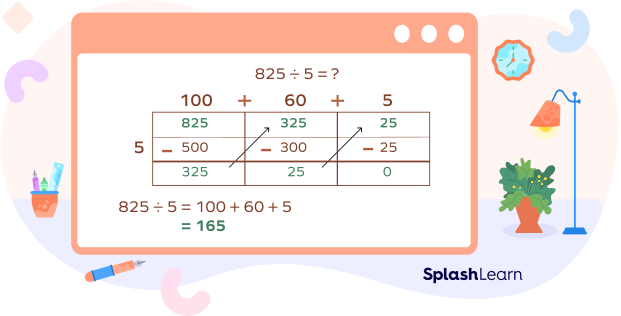
Step 1: Let’s start by breaking 825 into 500, 300, and 25, which are fairly easy to divide by 5.
Step 2: Now, let’s divide these partial dividends by the divisor 5 to get partial quotients:
500 divided by 5 gives us 100,
300 divided by 5 gives us 60,
and lastly, 25 divided by 5 gives us 5.
Step 3: Finally, let’s add all partial quotients to get the final quotient:
100 + 60 + 5 gives us 165. Now, we have our final product, which is 165.
Recommended Worksheets
Area Model Division with a Remainder
Sometimes, you’ll want to divide numbers that don’t divide evenly from one another. In these cases, it can be helpful to use an area model.
Let’s look at some division area model examples.
Divide 443 by 4 using area model division.
Step 1: Let’s break the numbers into 400, 40, and 3.
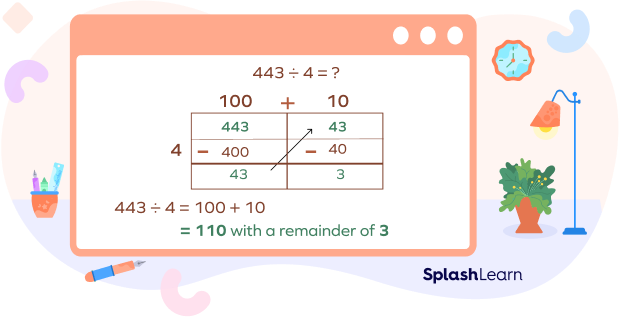
Step 2: Dividing 400 by 4, we get 100,
40 divided by 4 gives us 10,
Since 3 cannot be divided by 4, it will be our remainder.
Step 3: Now, we need to add 100 and 10 together to get a quotient, which gives us 110.
So, our final product is quotient $= 110$, remainder $= 3$.
Area Model for Dividing Decimal Numbers
Dividing decimal numbers can be challenging, but it doesn’t have to be. When you know how to use a few tricks like reducing decimals or using an area model, dividing decimals becomes much easier. Let’s learn the steps through area model division problems.
Divide 225.5 by 5 using area model
Step 1: We can divide the decimal numbers exactly like the regular ones by removing the decimal and adding it in the final step.
So instead of dividing 225.5 by 5, we will divide 2255 by 5.
Step 2: Now, let’s break them into easily divisible numbers, which are: 2000, 200, 50, and 5.
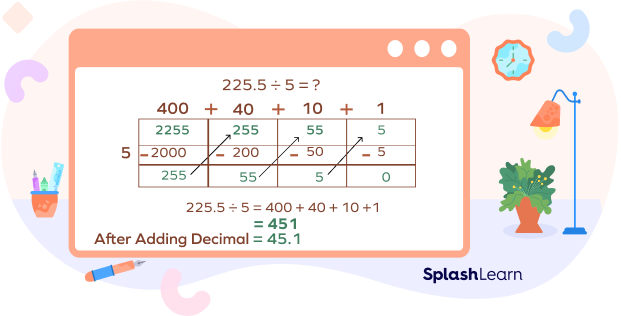
Step 3: Now, let’s divide each by 5:
2000 divided by 5 is 400
200 divided by 5 is 40
50 divided by 5 is 10
5 divided by 5 is 1
Step 4: Now, let’s add them together: $400 + 40 + 10 + 1$, giving us 451.
Step 5: Finally, let’s add the decimal we removed earlier. So, 451 will become 45.1, which is our final quotient.
Benefits of Using Area Model Division
1. It makes it easier to divide fractions or decimal numbers by multiplying them instead of trying to use long division with both parts.
2. It is a good way to help students remember how subtraction or “take away” works.
3. It helps students solve long divisions easily and also helps them understand the process of dividing numbers.
Solved Examples
1. Divide 728 by 14 using the area model.
Solution: Let’s start by breaking down 728 into 700 and 28.
Dividing 700 by 14 gives us 50, and 28 divided by 14 is 2.
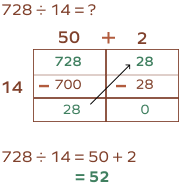
Now, let’s add these two to get the quotient $(50 + 2)$, which gives us 52.
2. Divide 624 by 3 using the area model of division.
Solution: Let’s start by breaking down 624, which gives us 600 and 24.
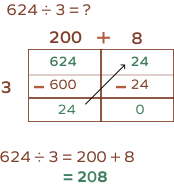
600 divided by 3 gives us 200, and 24 divided by 3 gives us 8.
On adding the two, we get 208.
3. Divide 3213 by 4 using the area model of division.
Solution: Let’s start by breaking down 3214, which gives us 3200 and 14.
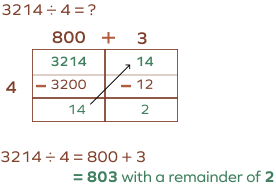
3200 divided by 4 gives us 800,
14 divided by 4 gives us 3, with a remainder of 2.
So, the final answer is 803, with a remainder of 2.
4. What is the quotient when you divide 4977 by 7 using area model?
Solution: First, let’s break down 4977 into 4900 and 77.
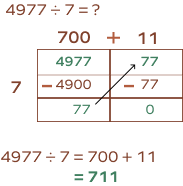
Dividing 4900 by 7, we get 700,
and 77 divided by 7 gives us 11
Adding these numbers $(700 + 11)$ gives us 711
So, the final answer is 711.
Practice Problems
Area Model Division
What is the quotient when you divide 345 by 5 using the area model?
Let’s start by breaking down the numbers, which gives us 300 and 45.
Now, let’s divide them individually.
300 divided by 5 is 60,
45 divided by 5 is 9,
Adding all these numbers together (60 + 9) gives us 69.
So, the quotient is 69.
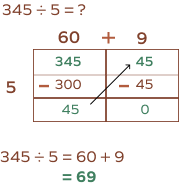
What is the answer when you divide 246 by 4 using the area model?
On breaking down 246, we get: 200, 44, and 2.
200 divided by 4 is 50,
44 divided by 4 is 11,
and 2 can not be divided by 4, so it will be a remainder.
On adding 50 and 11, we get 61.
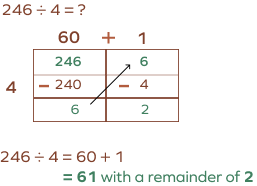
What is the quotient when you divide 29.7 by 3 using the area model?
First, let’s start by removing the decimal, which makes $29.7 = 297$
Let’s break down 297 into 270 and 27.
Dividing 270 by 3, we get 90,
and 27 divided by 3 gives us 9.
Adding these numbers $(90 + 9)$ gives us 99
Using the decimal point makes it 9.9
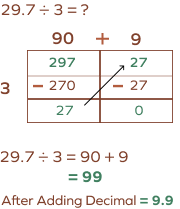
What is the quotient when you divide 69.20 by 4 using the area model?
First, let’s start by removing the decimal, which makes $69.20 = 6920$
Let's break down 6920 into 6800 and 120.
Dividing 6800 by 4, we get 1700,
and dividing 120 by 4 gives us 30.
Adding these numbers $(1700+30)$ gives us 1730
Using the decimal point makes it 17.30
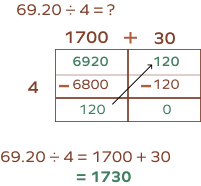
Frequently Asked Questions
Can area model division be used for fractions?
Yes, you can efficiently use area model division to divide fractions.
Can the area model be used for multiplication?
Yes, you can use area models to solve a multiplication problem with large numbers. The multiplicands will be the length and breadth of a rectangle, and their product will be the area of the rectangle.
To find the area, you divide the rectangle into smaller segments. The sum of the areas of the smaller rectangles gives you the total area, which will be the product. This method is also called box multiplication.
What is the purpose of the area model division?
Area model division helps students visualize and make longer division problems easier to solve.
Why is the area model for division important?
Division using area models gives students another perspective on math equations, which is extremely valuable since not all kids (or adults) think in the same way.