What Are Benchmark Fractions?
Benchmark fractions are fractions that are easy to identify and visualize. Let’s understand this using a real-life example. What do you do when you are trying to find a new address or when you explore a new street? You try to identify a benchmark near it or a nearby location you are familiar with and then you find the new address comparing it against the benchmark point.
Similarly, when comparing or ordering fractions becomes difficult, we can take help from benchmark fractions. Let’s brush up some basic concepts first!
A fraction can be defined as a part of a whole. The denominator represents the total number of equal parts of a whole and is written at the bottom. The numerator represents the number of parts taken from the whole and is written at the top.
$\frac{3}{5}$ represents 3 parts out of 5 equal parts. 3 is the numerator, and 5 is the denominator.
Recommended Games
Benchmark Fractions Definition
In math, benchmark fractions can be defined as fractions that we can use when measuring, comparing, or ordering other fractions. They are used as a “benchmark” for other common factors.
Common benchmark fractions examples: $0, 1,\frac{1}{4} , \frac{1}{2}$ , etc.
These fractions are most helpful when the fractions are to be compared or to be placed on a number line. Here’s a benchmark fractions chart placed on a number line, which can help you compare fractions:
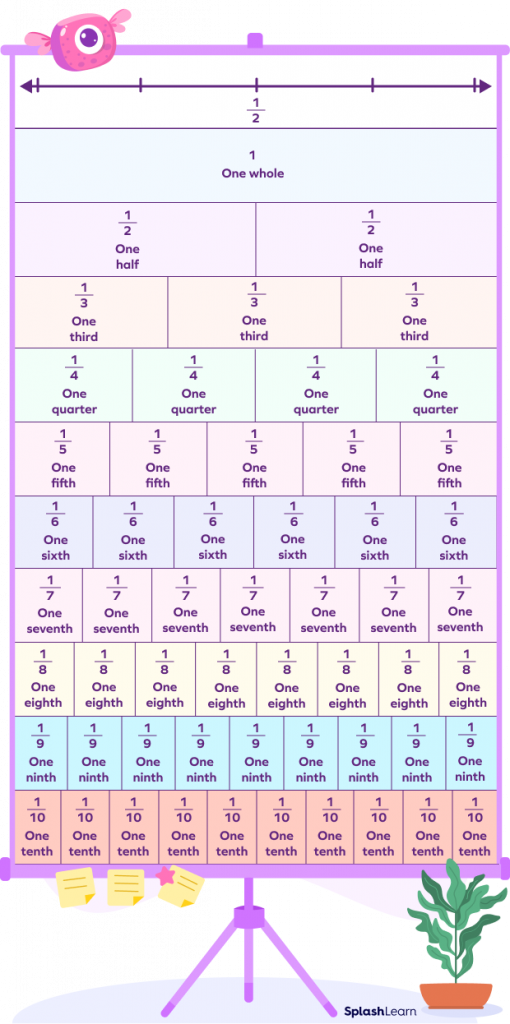
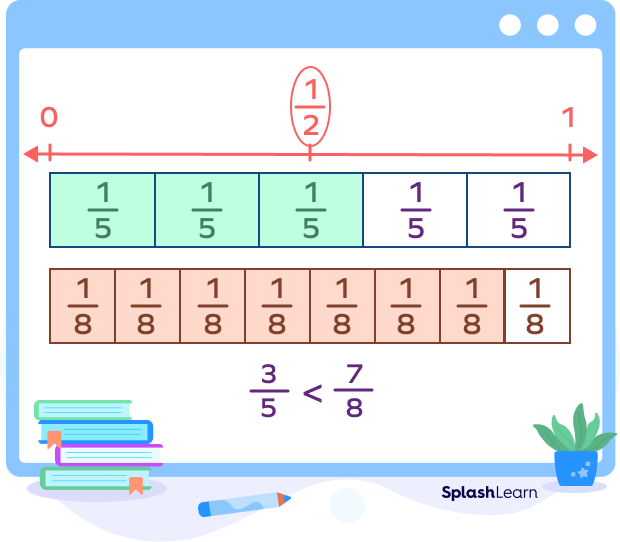
Let’s understand how the fraction strip is helpful. Let’s compare the unlike fractions $\frac{3}{5}$ and $\frac{7}{8}$ easily using this chart.
Observe the one-fifth strip and the one-eighth strip. The 3 parts of the one-fifth strip represent 35and the 7 parts of the one-eighth strip $\frac{7}{8}$. Comparing the region occupied by the shaded parts, we get $\frac{3}{5} \lt \frac{7}{8}$.
Recommended Worksheets
How to Compare Fractions Using Benchmark Fractions
The benchmark chart can be used to compare two or more fractions, considering the length of the corresponding fractions. The process is comparable to using fraction strips for approximating measurements.
The most common benchmark fraction is $\frac{1}{2}$. It is right in the middle of zero and one. It can also be written in the equivalent fraction form as $\frac{2}{4}, \frac{3}{6}, \frac{4}{8}$, and so on.
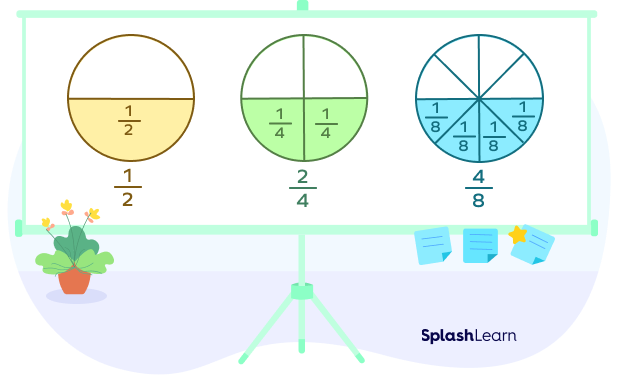
If the numerator is half of the denominator, then the fraction is equivalent to $\frac{1}{2}$.
If a fraction is equivalent to $\frac{1}{2}$, its position on the number line will be the same as $\frac{1}{2}$.
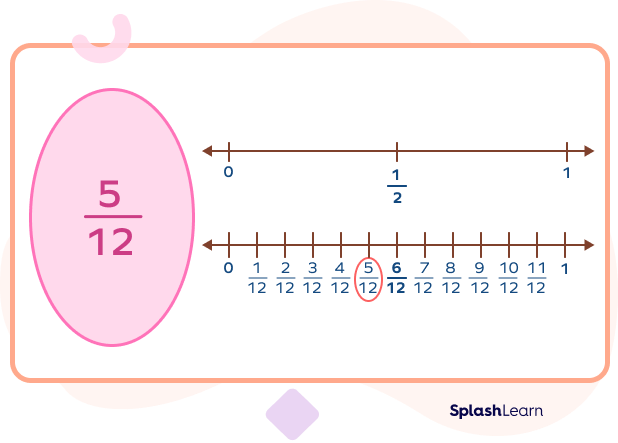
Example 1: Let’s find out if the fraction $\frac{5}{12}$ is less than $\frac{1}{2}$ or greater than $\frac{1}{2}$ or equals $\frac{1}{2}$.
What’s the equivalent fraction of $\frac{1}{2}$ closer to $\frac{5}{12}$? It’s $\frac{6}{12}$.
So, $\frac{6}{12} = \frac{1}{2}$
It is clear that $\frac{5}{12} \lt \frac{6}{12}$ since the denominator is the same and $5 \lt 6$.
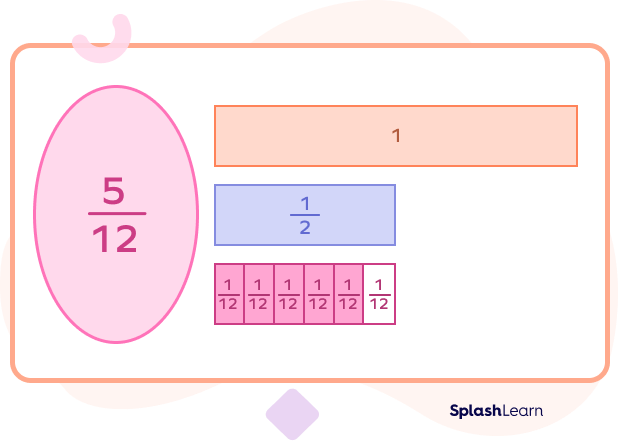
So, what do we know? $\frac{5}{12}$ is less than $\frac{6}{12}$ and $\frac{6}{12}$ equals $\frac{1}{2}$.
We can easily conclude that $\frac{5}{12}$ is less than $\frac{1}{2}$.
We know that $\frac{4}{16} = \frac{1}{4}$.
Also, $\frac{5}{16}$ is greater than $\frac{4}{16}$.
So, we can say that $\frac{5}{16}$ is greater than $\frac{1}{4}$.
Using Benchmark Fractions for Rounding Fractions
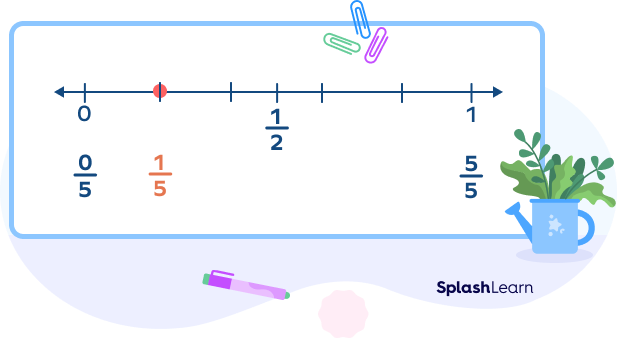
1. If the numerator is much smaller than the denominator, we round the given fraction to 0
Example: $\frac{1}{9}, \frac{1}{5}$ can be rounded to 0 since they are much closer to 0 on a number line.
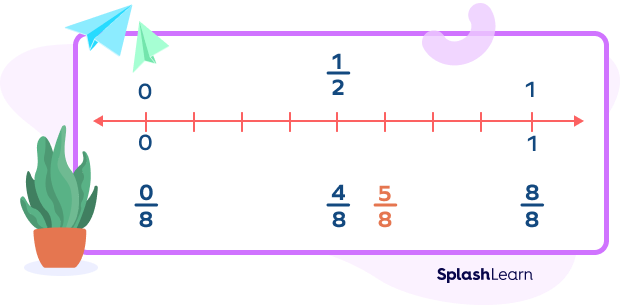
2. If the numerator is almost half of the denominator, then we round the given fraction to $\frac{1}{2}$.
Example: $\frac{5}{11}, \frac{2}{6}, \frac{5}{8}$ can be rounded to $\frac{1}{2}$.
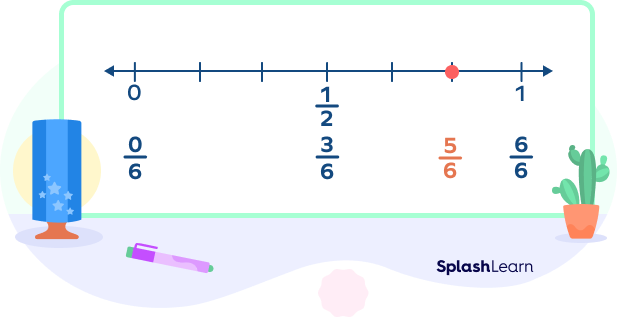
3. If the numerator and denominator are almost equal, then we round the given fraction to 1.
Example: $\frac{10}{11}, \frac{5}{6}$ can be rounded to 1.
Let’s Sing!
When comparing or ordering two different fractions,
Let benchmark fractions be your guiding action!
Just begin by putting the fractions on a number line.
Then, choose the benchmark to compare—it’ll be fine!
Solved Examples
1. Compare $\frac{5}{8}$ and $\frac{1}{2}$.
Solution: We already know that $\frac{4}{8}$ is an equivalent fraction of $\frac{1}{2}$.
Since 5 is greater than 4, we can say that $\frac{5}{8}$ is greater than $\frac{4}{8}$.
So, $\frac{5}{8}$ is greater than $\frac{1}{2}$.
2. Compare whether $\frac{2}{6}$ is less or more than $\frac{2}{3}$.
Solution: $\frac{2}{6}$ is an equivalent fraction of $\frac{1}{3}$.
So, $\frac{2}{6} = \frac{1}{3}$.
Since $\frac{1}{3}$ is less than $\frac{2}{3}, \frac{2}{6}$ is less than $\frac{2}{3}$.
3. Which is greater: $\frac{4}{8}$ or $\frac{6}{12}$?
Solution: $\frac{4}{8}$ can also be written as $\frac{1}{2}$.
$\frac{6}{12}$ can also be written as $\frac{1}{2}$.
So, this means both fractions are equal.
Practice Problems
Benchmark Fractions - Definition with Examples
Which fraction is closer to $0: \frac{1}{2} ,\frac{1}{4}$ or $\frac{3}{4}$ ?
$\frac{1}{2}$ is the midpoint of 0 and 1.
$\frac{1}{4}$ is exactly in the middle of 0 and $\frac{1}{2}$.
$\frac{3}{4}$ is exactly in the middle of $\frac{1}{2}$ and 1.
So, $\frac{1}{4}$ is closer to 0.
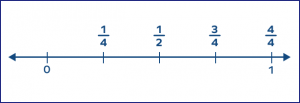
Compare the fractions $\frac{1}{4}$ and $\frac{3}{12}$.
On simplifying $\frac{3}{12}$, we get $\frac{1}{4}$.
Therefore,$\frac{1}{4} = \frac{3}{12}$
Which is greater among $\frac{12}{18}, \frac{14}{21}$, and $\frac{18}{27}$?
$\frac{12}{18}$ can be simplified as $\frac{2}{3}$.
$\frac{14}{21}$ can be simplified as $\frac{2}{3}$.
$\frac{18}{27}$ can be simplified as $\frac{2}{3}$.
This means all three are equal.
Compare $0, \frac{2}{6}$ and $\frac{6}{9}$.
Both the fractions are greater than 0 since they are positive.
$\frac{2}{6}$ can be simplified as $\frac{1}{3}$.
$\frac{6}{9}$ can also be written as $\frac{2}{3}$.
Since $\frac{2}{3} \gt \frac{1}{3}$, we can say that $\frac{6}{9} \gt \frac{2}{6}$.
Frequently Asked Questions
What is the purpose of using fraction strips?
Fraction strips are a practical way for students to grasp the fundamentals of fractions. Fraction strips simplify studying the division of fractions into halves, thirds, quarters, etc.
For example, these strips can be cut into various sizes, so it’s possible to work on multiple problems. They are especially useful for understanding addition, subtraction, and multiplication.
What is the easiest way of comparing fractions?
Converting fractions to decimal numbers makes it much easier to determine which fraction is larger. The fraction with the larger decimal value is the greater the fraction.
What does comparing fractions mean?
You compare the two fractions to determine if one is less than, greater than, or equal to the other.
What are benchmark numbers?
Benchmark numbers are numbers that are used to compare other numbers or quantities. They also help in estimation problems. Common example of benchmark numbers is multiples of 10 or 100.




































