Multiplying Mixed Numbers – Definition With Examples

What Are Mixed Numbers

A mixed number is a whole number and a proper fraction represented together.  It generally represents a number between any two whole numbers. 

Look at the given image, it represents a fraction that is greater than 1 but less than 2. It is thus a mixed number. 

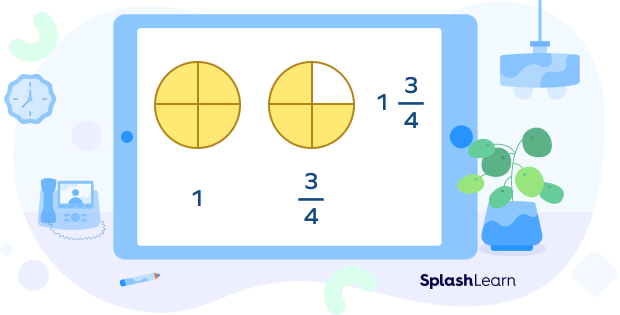
Some other examples of mixed numbers are: 

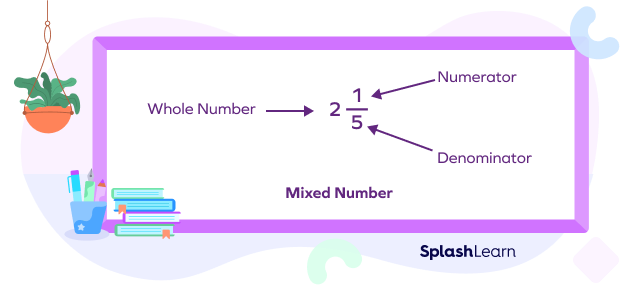
Parts of a mixed number

A mixed number is formed by combining three parts: a whole number, a numerator, and a denominator. The numerator and denominator are part of the proper fraction that makes the mixed number.

Converting Mixed Numbers to Improper Fractions

• Multiply the whole number by the denominator of the fraction.
• Add the answer obtained from Step 1 to the numerator of the fraction. 
• Write an answer obtained from Step 2 over the denominator.

Let us suppose we have to convert $2\frac{2}{3}$ into an improper fraction.

Step 1: Multiply 3 and 2, we get $3 \times 2 = 6$.

Step 2: Add 6 and 2, we get $6 + 2 = 8$

Step 3: The fraction obtained is $\frac{8}{3}$. 

Multiplying a Mixed Number by a Whole Number

Step 1: Convert the mixed number into an improper fraction.

Step 2: Rewrite the whole number as a fraction with the denominator 1.

Step 3: Multiply two fractions by multiplying the numerators and denominators separately.

Step 4: Convert it into simplified form if required.

Suppose we have to multiply 3 and $2\frac{1}{2}$.

$2\frac{1}{2}=\frac{2\times2+1}{2}=\frac{5}{2}$

$3\times\frac{5}{2}=\frac{3}{1}\times\frac{5}{2}=\frac{15}{2}=7\frac{1}{2}$

Multiplying a Mixed Number by a Fraction

Step 1: Convert the mixed number into an improper fraction.

Step 2: Multiply the numerators of the fraction and multiply the denominators of the fraction.

Step 3: Convert it into simplified form if required.

Suppose we have to multiply $\frac{2}{5}$ and $3\frac{1}{2}$.

$3\frac{1}{2}=\frac{3\times2+1}{2}=\frac{7}{2}$

$\frac{2}{5}\times\frac{7}{2}=\frac{14}{10}=\frac{7}{5}=1\frac{2}{5}$

Multiplying Two Mixed Numbers

Step 1: Convert the mixed numbers into improper fractions.

Step 2: Multiply the two fractions by multiplying the numerators and denominators separately.

Step 3: Convert it into simplified form if required.

For example: Multiply $4\frac{1}{2}$ and $3\frac{1}{3}$.

$4\frac{1}{2}=\frac{4\times2+1}{2}=\frac{9}{2}$

$3\frac{1}{3}=\frac{3\times3+1}{3}=\frac{10}{3}$

$4\frac{1}{2}\times3\frac{1}{3}=\frac{9}{2}\times\frac{10}{3}=\frac{90}{6}=15$ 

Conclusion

In this article, we learnt about multiplying mixed numbers. Mixed numbers are also known as mixed fractions. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.

Solved Examples

1. Multiply $5\frac{3}{7}$ by the multiplicative inverse of $7\frac{3}{5}$. 

Solution: $5\frac{3}{7}=\frac{5\times7+3}{7}=\frac{38}{7}$

$7\frac{3}{5}=\frac{7\times5+3}{5}=\frac{38}{5}$

Multiplicative inverse of $\frac{38}{5}$ is $\frac{5}{38}$.

Product $= \frac{38}{7}\times\frac{5}{38}=\frac{5}{7}$

2. Emma walks 523 miles in a day. How much distance will she cover in 9 days?

Solution: Distance traveled by Emma in 1 day $= 5\frac{2}{3}$miles$=\frac{17}{3}$ miles.

Distance traveled by Emma in 9 days $= 9\times\frac{17}{3}= 51$ miles 

3. Multiply $6\frac{2}{5}\times\frac{3}{4}$.

Solution: $6\frac{2}{5}=\frac{6\times5+2}{5}=\frac{32}{5}$

$\frac{32}{5}\times \frac{3}{4}=\frac{32\times3}{5\times4}=\frac{96}{20}=\frac{24}{5}=4\frac{4}{5}$

Practice Problems

Frequently Asked Questions