What is a Prism?
A prism is a three-dimensional solid figure with flat faces and two identical bases. The two bases of a prism are polygons like a triangle, a square, a rectangle, or a hexagram. A prism is usually named after the polygon that forms its base.
For example, a triangular prism has two triangles as its bases.

A rectangular prism has two rectangles as its bases.

Based on this, can you guess what a hexagonal prism is?
What is a Hexagonal Prism?
A hexagonal prism is defined as a prism with a hexagonal base and top. A hexagonal prism has 8 faces, 18 edges, and 12 vertices.
Out of the 8 faces, 6 are parallelograms, and 2 are hexagons, and that’s why it is called a hexagonal prism. These hexagons are at the base and the top as the opposite faces of a prism are the same.
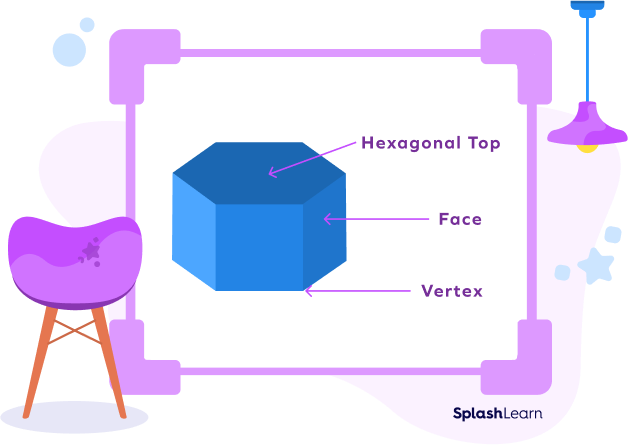
Alt Tag: Solid hexagonal prism marked with base, face, and vertex
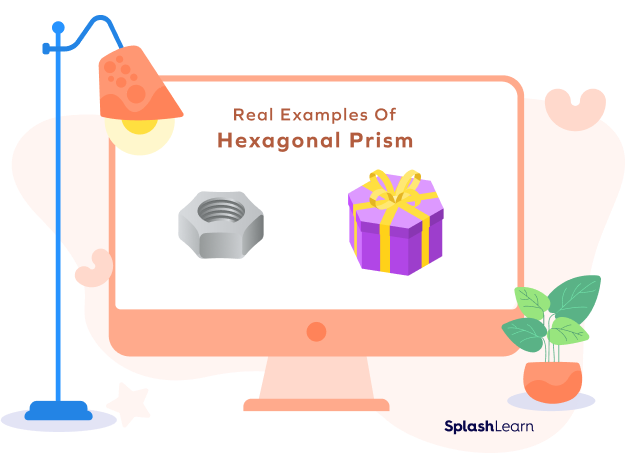
Real-Life Examples of Hexagonal Prisms
Hexagonal prisms might not be as common as other prisms, but they can still be found around us. Some of its examples are boxes, nuts, pencils, weights, buildings, vases, etc.
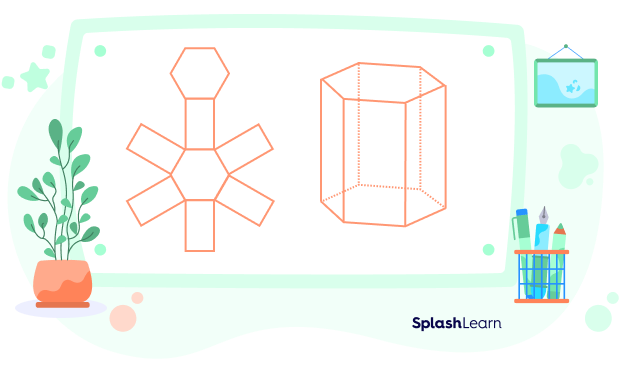
Net of a Hexagonal Prism
We can form a hexagonal prism using its net, as shown below.
The net of a 3D object shows the faces of that object when it is opened flat. On folding the net, we get the 3D object.
How to Calculate the Volume of a Hexagonal Prism?
The volume of a hexagonal prism refers to the space that it occupies. The volume of any prism can be calculated with this equation:
Volume = base area × height of the prism
The base area is the surface area of the polygon base. In this case, it is the hexagon.
It is measured in square units (like square inches or square feet) because it describes the surface area.
The height is the column that connects the two bases of the prism. It is measured in single units (like inches or feet) since it describes the length of the column.
When you multiply the base area with the height, the resulting value is in cubic units, like cubic inches, cubic yards, cubic feet, or cubic meters. These units measure the volume of a three-dimensional figure.
Fun Fact
The hexagonal face of a hexagonal prism can either be a regular hexagon or an irregular hexagon. If it is a regular hexagon, then all the angles of the hexagon are the same. If it is an irregular hexagon, then the angles of the hexagon are different.
Solved Examples
Example 1. How many total faces does a hexagonal prism have?
Alt Tag: Hexagonal prism
Answer. A hexagonal prism has 8 faces in total – two bases and 6 sides.
Example 2. What polygons make up the sides of a hexagonal prism?
Answer. The sides of a hexagonal prism are parallelograms or rectangles.
Example 3. The base of a hexagonal prism has a surface area of 475 inch². The height is 8 inches. Calculate the volume.
Answer. Volume = base area × height
Base area = 475 inch²
Height = 8 inches
Volume = 475 × 8 = 3800 inch³
Example 4. The volume of a hexagonal prism is 150 inch³. The surface area of the base is 10 inch². What is the height?
Answer. Volume = base area x height
Volume = 150 inch³
Surface area = 10 inch²
150 = 10 × height
Height =150/10 = 15
So, the height is 15 inches.
Practice Problems
Hexagonal Prism - Definition With Examples
How many edges and vertices does a hexagonal prism have?
A hexagonal prism has 18 edges and 12 vertices.
The base of a hexagonal prism has a surface area of 250 inch². The height is 20 inches. Calculate the volume.
Base area = 250 inch²
Height = 20 inches
Volume = base area x height
= 250 × 20
Volume = 5000 inch³
The volume of a hexagonal prism is 250000 cm³. The surface area of the base is 1000 cm². What is the height?
Volume = 250000 cm³
Base area = 1000 cm
Volume = base area × height
250000 = 1000 × height
Height = 250000/1000
= 250 cm
Frequently Asked Questions
Why is a hexagonal prism said to be a polyhedron?
A polyhedron is a three-dimensional figure in which all the faces are polygons. It has flat faces, straight edges, and vertices.A cube, a prism, and a pyramid are all examples of polyhedrons. A hexagonal prism is made up of 6 rectangles and two hexagons. Since all its faces are polygons, it is considered a polyhedron.
Why is a hexagonal prism said to be an octahedron?
An octahedron is a polyhedron that has 8 faces. A hexagonal prism has 8 faces (including its 2 bases and 6 sides), so it is an octahedron.
A common example of an octahedron is a regular octahedron, in which the faces are 8 regular triangles.

What are irregular hexagonal prisms?
Irregular hexagonal prisms are those that have irregular hexagons as their bases. In other words, the two base hexagons have different angles, and the sides are not equal in length.

















