Like and Unlike Algebraic Terms – Definition, Facts, Examples, FAQs

What Are Like and Unlike Terms in Algebra?

Like terms and unlike terms in algebra are two important concepts that are very crucial when we carry out operations like addition and subtraction on algebraic expressions/ equations.

The smaller individual expressions separated by the arithmetic operations to complete the larger or whole algebraic expression or equation are called algebraic terms.

What Are Like Terms?

Like terms in algebra are the terms in an expression whose variable part is the same and also the corresponding exponents for each variable are equal. The coefficient of these variables can be different.

In simple words, the variable part of the “like terms” look exactly the same. Same variables are raised to the same powers. 

In addition or subtraction, or when simplifying algebraic expressions, we always combine like terms.

Like terms examples: 

• x and 2x are like terms. 
• st and -5st are like terms.
• $xy^{2} z^{7}$ and $65xy^{2}z^{7}$ are like terms.
• abc and 2abc are like terms.
• 5 and 9 are like terms.

What Are Unlike Terms?

Unlike terms can be defined as the algebraic terms whose variable part is totally different, or the variables are the same but their exponents are different.

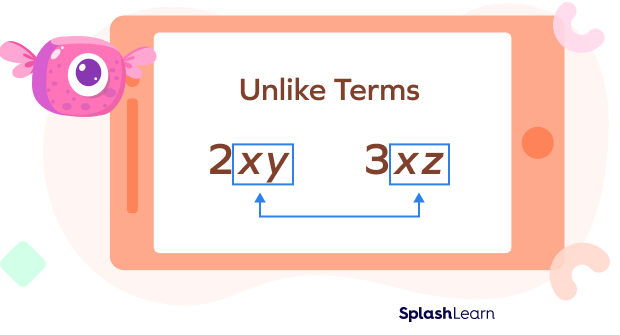
We cannot add or subtract two unlike terms. So, we always keep them separate.

Unlike terms examples: 

• x and y are like terms. 
• xy and $-2x^{3}y$ are like terms.
• 6abc and 6pq are like terms.
• xyz and $x^{2}yz$ are like terms.

How to Identify Like Terms and Unlike Terms

We can identify like and unlike terms by simply checking the variables and their powers.

Like Terms	Unlike terms
s, 2s, -4s, 10s, 999s, -999s	$a,\; ab,\; a^{2}b,\;pqr,\;m^{6}n^{7}$
$x^{2},\; -7x^{2},\; 90x^{2},\; 12345x^{2},\; -x^{2}$	$x, y, x^{2} y^{2}$

Visualizing Like and Unlike Terms

Now, you know how to identify like terms and unlike terms. There’s also an interesting visual approach to understand like and unlike terms. Let’s check it out!

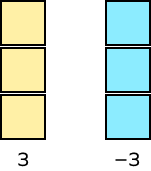	3 and -3 are like terms. Both are constants. Signs do not matter. The coefficients of like terms can be different (Here, the coefficients are 1 and -1).Here, the variable part does not exist in both the terms.
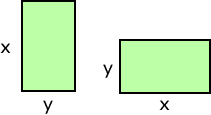	xy and yx are like terms.  Basically, xy = yx  They have the same meaning.  The order of the multiplication does not matter.
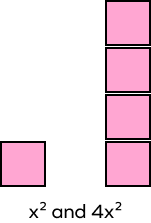	Can you see the similarity in the patterns formed by the like terms?  $x^{2}$ and $4x^{2}$ are like terms.  Coefficients of like terms can be different.  The variable part must be the same.
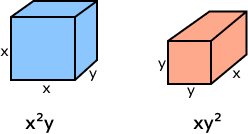	Now, take a look at the visual representation of unlike terms. They do not look similar. $x^{2} y$ and $xy^{2}$ are unlike terms.  The variable parts do not match.

Addition and Subtraction of Like Terms

We can simplify algebraic expressions or equations by combining the like terms for addition or subtraction. Note that when we combine like terms, we take their signs along with them.

To add like terms, only focus on the coefficients. Add the coefficients and keep the variable part as it is. The variables stay the same. 

Similarly, to subtract like terms, subtract the coefficients and keep the variables the same.

Also, you must follow the rules of addition and subtraction keeping the signs of the terms in mind.

Example 1:

• 8x² – 5x² = (8 – 3)x² = 5x²
• 11z + 13z + 16z = (11 + 13 + 16)z = 40z
• -9+5=-4

Example 2: Simplify x + y – x²y + 7y – 87x – xyz + 11x²y – 9 + 8x.

Combine the like terms.

x + y – x²y + 7y – 87x – xyz+ 11x² y – 9 + 8x

= (x + 8x – 87x) + (y + 7y) – x²y + 11x²y – xyz – 9

= 78x + 8y + 10×2²y – xyz – 9 

Addition and Subtraction of Unlike Terms

The simplification of expressions or combining like terms cannot be done on unlike terms, as the variables and exponents are not similar. 

Consider an algebraic expression, 8xy + 6y – 9x – 10x². There are different variables, exponents, and coefficients. This expression cannot be simplified as all the terms are different from each other.

Difference Between Like and Unlike Terms

Following is the difference between like and unlike terms: 

Like Terms	Unlike Terms
Terms with the same variables raised to the same exponents.	Terms with different variables or same variables with different exponents.
Like terms can be simplified by combining them.	Unlike terms cannot be simplified by combining them.
Addition and Subtraction of like terms can be done.	Addition and Subtraction of unlike terms cannot be done.
13x2 + 5x2 is an example of like terms.	7z – 25r is an example of unlike terms.
Like terms are also called similar terms.	Unlike terms are also called dissimilar terms.

Conclusion

In this article, we learned about like and unlike terms, which are essential concepts in algebraic expressions. Understanding the distinction between these terms is crucial for simplifying expressions and solving equations. Let’s reinforce our knowledge by solving examples and practicing MCQs for better comprehension.

Solved Examples on Like and Unlike Terms

1. Identify like terms in the algebraic expression 7x – 8y + 10x – 26y.

Solution: 

The like terms are the terms with the same variable and the same power. 

So, the like terms are: 

• 7x and 10x 
•  – 8y and – 26y. 

2. Simplify 5x + 8y.

Solution: 

We can not simplify 5x + 8y any further since 5x and 8y are unlike terms. 

3. Simplify: 2x² + 6x + 4y + 3x + 15x²

Solution: 

2x² + 6x + 4y + 3x + 15x²

Combining the like terms, we get

= (2x² + 15x²) + (6x + 3x) + 4y

= 17x² + 9x + 4y

4. What should be added to 5x² – 2x to get 2x² + 3x – 1?

Solution: 

Let ‘a’ be the expression added to 5x² – 2x to get 2x² + 3x – 1. 

a + 5x² – 2x = 2x² + 3x – 1

a = 2x² + 3x – 1 – (5x² – 2x)

a = 2x² + 3x – 1 – 5x² + 2x

a = (2x² – 5x²) + (3x + 2x) – 1

a = – 3x² + 5x – 1

5. Simplify the expression: 20xy – 16yx. 

Solution: 

The variables and the power in 20xy and 16yx are the same. 

The only difference is the order. 

Since the multiplication is commutative, 20xy and – 16yx are like terms. 

20xy – 16yx = 4xy = 4yx

Practice Problems on Like and Unlike Terms

Frequently Asked Questions about Like and Unlike Terms