What Is a Linear Pair Of Angles?
A linear pair of angles is a pair of adjacent angles formed when two lines intersect each other at a single point.
“Linear” simply means “arranged along a straight line.” We know that a straight angle is an angle that measures $180^\circ$. It is called a straight angle because it appears as a straight line. Two angles formed along a straight line represent a linear pair of angles.
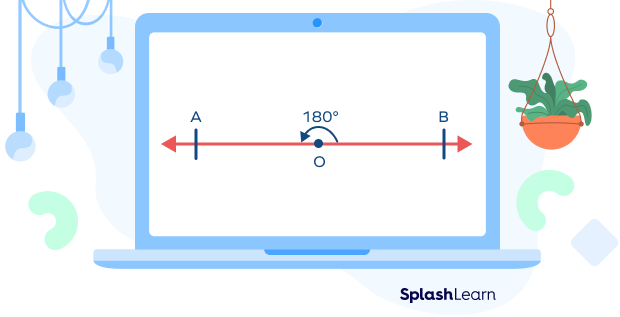
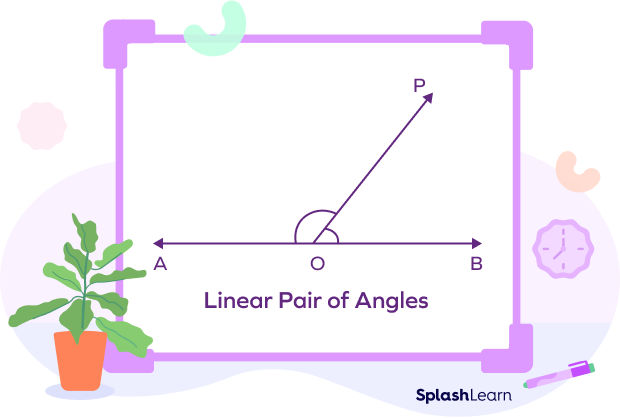
In the diagram shown below, $\angle POA$ and $\angle POB$ form a linear pair of angles. They add up to $180^\circ$. In other words, they are supplementary.
$\angle POA + \angle POB = 180^\circ$
Observe that these angles have one common arm (OP), which makes them adjacent angles. Also, their non-common sides OA and OB are opposite rays.
Examples of Linear Pair of Angles:
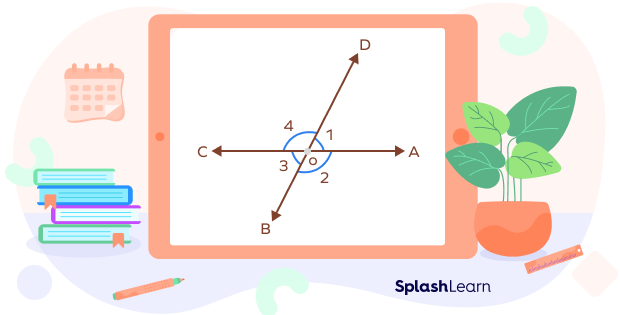
1) In the figure given below, the linear pair of angles are:
$\angle 1 ,\; \angle 4$
$\angle 1 ,\; \angle 2$
$\angle 3 ,\; \angle 2$
$\angle 3,\; \angle 4$
2) Here, $\angle ADC$ and $\angle BDC$ form a linear pair of angles.

Recommended Games
Definition of Linear Pair of Angles in Geometry
Two angles are said to form a linear pair if
- they are adjacent angles
- their non-common arms are opposite rays & form a straight line
Recommended Worksheets
Properties of Linear Pair of Angles
- The angles in a linear pair are supplementary (add up to $180^\circ$).
- A linear pair of angles are always adjacent angles.
- A linear pair of angles always form a straight line.
- They together form a straight angle.
- Two angles forming a linear pair have a common vertex and a common arm. Their non-common sides are opposite rays that form a line.
Linear Pair Postulate
The linear pair postulate states that if two angles form a linear pair, they are supplementary.
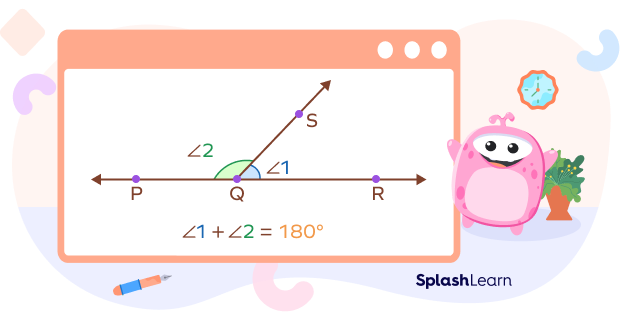
The converse of this postulate is not true. It means that if two angles are supplementary, they do not necessarily form a linear pair of angles.
Counter example:
In the image below, angles M and N are supplementary since
$120^\circ + 60^\circ = 180^\circ$
However, they do not form a linear pair of angles. They are not adjacent.
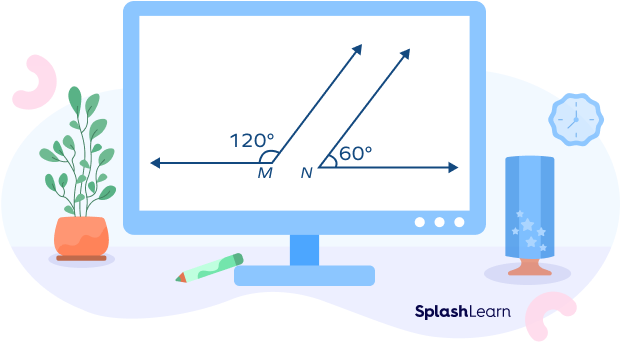
Linear Pair Axioms
Let’s learn two important axioms which are collectively termed as ‘linear pair axioms’. Axiom is a mathematical statement that is self-evident and accepted to be true.
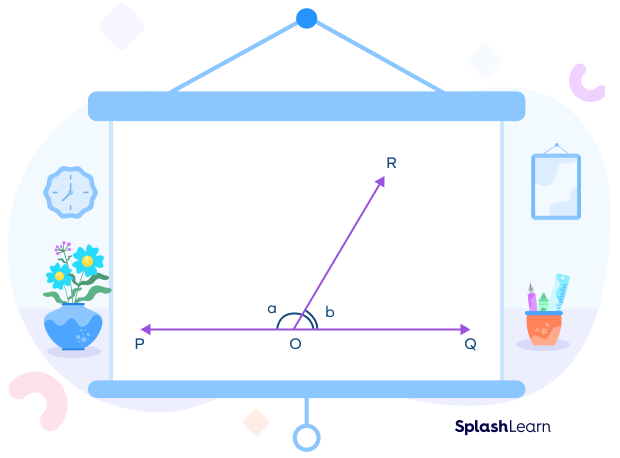
Axiom 1: If a ray stands on a line, then the sum of two adjacent angles formed is $180^\circ$.
The ray OC is standing on a line AB. Thus, the adjacent angles $\angle AOC$ and $\angle BOC$ add up to $180^\circ$.
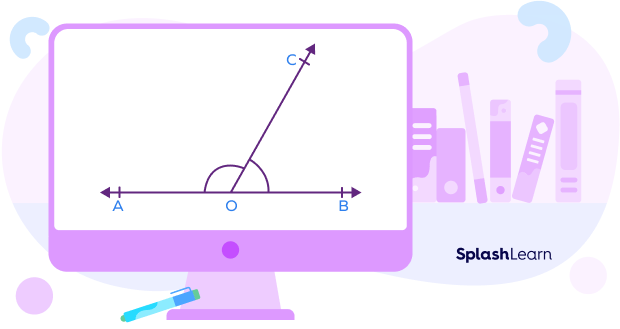
The converse of the axiom 1 is also true.
Axiom 2: If two angles form a linear pair, then non-common arms of both the angles form a straight line.
In the diagram shown above, the rays OA and OB are the non-common arms of the angles $\angle AOC$ and $^\circ BOC$. Rays OA and OB form a straight line AB.
Linear Pair Perpendicular Theorem
If two angles forming a linear pair of angles are congruent, then the lines are perpendicular.
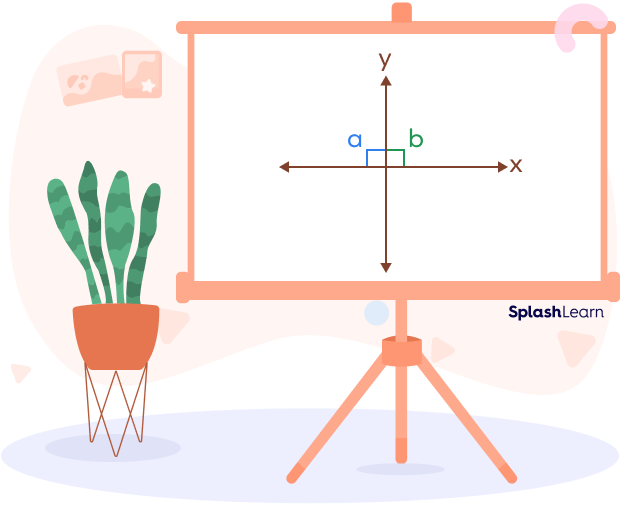
Here, the angles $\angle a$ and $\angle b$ form a linear pair of angles. Also, they are congruent since they measure 90 degrees each.
Thus, the lines x and y are perpendicular to each other.
Linear Pair of Angles vs. Supplementary Angles
It is the most common mistake to confuse supplementary angles with linear pairs of angles due to similarity in their properties. However, these are two different terms. Let’s understand the difference.
| Linear Pair of Angles | Supplementary Angles |
|---|---|
| A linear pair of angles are always adjacent angles. They have a common vertex and a common arm. | Two supplementary angles may or may not be adjacent. |
| These are adjacent angle that add up to $180^\circ$ | These are any two angles that add up to $180^\circ$ |
| All linear pairs of angles are supplementary angles. | Supplementary angles need not form a linear pair of angles. |
 |  |
Solved Examples on Linear Pair of Angles
1. Observe the diagram and identify the linear pair of angles.
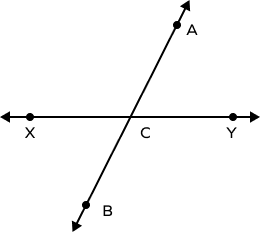
Solution:
The lines AB and XY intersect at a single point C.
Thus, they form linear pairs of angles.
Any two adjacent angles formed here will form a linear pair of angles.
Angles in linear pair are:
- $\angle ACY$ and $\angle BCY$
- $\angle ACX$ and $\angle ACY$
- $\angle ACX$ and $\angle BCX$
- $\angle BCX$ and $\angle BCY$
2. If two angles forming a linear pair are in the ratio of 7:11, then find the measure of each of the angles.
Solution:
Let the measures of the angles be $(7x)^\circ$ and $(11x)^\circ$.
Since the angles form a linear pair, we can write
$(7x)^\circ + (11x)^\circ = 180^\circ$
$(18x)^\circ = 180$
$x = 10$
Two angles are $7 \times 10 = 70^\circ$ and $11 \times 10 = 110^\circ$
3. Angles $^\angle ABC$ and $^\angle DBC$ form a linear pair of angles. Find the measure of $\angle ABC$ in the following figure.
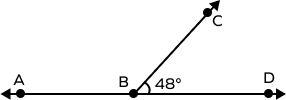
Solution:
Since the angles form a linear pair, they are supplementary.
$m\angle ABC + m\angle DBC = 180^\circ$
$m\angle ABC + 48^\circ = 180^\circ$
$m\angle ABC = 180^\circ \;-\; 48^\circ$
$m^\circ ABC = 132^\circ$
4. If one angle in the linear pair is $40^\circ$, then find the other angle.
Solution:
Measure of one angle $= 40^\circ$
Since the angles form a linear pair, they add up to $180^\circ$.
Measure of the other angle $= 180^\circ \;–\; 40^\circ = 140^\circ$
5. One angle of the linear pair is thrice the other. Find the angles.
Solution:
Let one angle be $x^\circ$ and the other angle be $3x^\circ$.
Since they form a linear pair, we write
$x^\circ + 3x^\circ = 180^\circ$
$4x^\circ = 180^\circ$
$x^\circ = 45^\circ$
Thus, the angles are $45^\circ$ and $135^\circ$.
6. Do angles that measure $107^\circ$ and $72^\circ$ form a linear pair?
Solution:
Angles in a linear pair are supplementary. So, if two angles are not supplementary, they are not a linear pair of angles.
$107^\circ + 72^\circ = 179^\circ 180^\circ$
They do not form a linear pair.
Practice Problems on Linear Pair of Angles
Linear Pair of Angles: Definition, Axioms, Examples, Facts, FAQs
Which of the following is the linear pair of $75^\circ$?
Linear pair of $75^\circ = 180^\circ \;–\; 75^\circ = 105^\circ$
What will be the value of x?
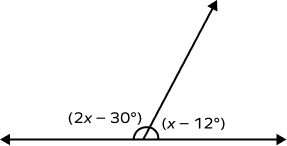
The angles measuring $(2x \;–\; 30)$ and $(x \;–\; 12)$ form a linear pair.
$2x \;–\; 30 + x \;–\; 12 = 180^\circ$
$3x \;–\; 42 = 180^\circ$
$3x = 222^\circ$
$x = 74^\circ$
Which of the following pairs of angles form a linear pair?
$123^\circ + 57^\circ = 180^\circ$. They form a linear pair.
$145^\circ + 25^\circ = 170^\circ$. They do not form a linear pair.
$125^\circ + 45^\circ = 170^\circ$. They do not form a linear pair.
$109^\circ + 70^\circ = 179^\circ$. They do not form a linear pair.
Which of the following pairs of angles form a linear pair?
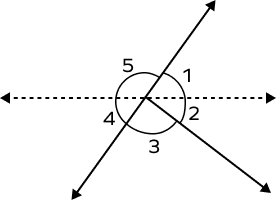
$\angle1$ and $\angle4$ are not adjacent angles.
$\angle2$ and $\angle3$ are adjacent angles but are not supplementary.
$\angle3$ and $\angle5$ are not adjacent.
$\angle1$ and $\angle5$ are adjacent angles and are supplementary. Thus, they form a linear pair.
What will be the value of k in the following figure?
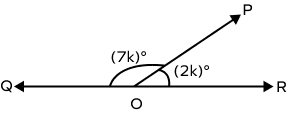
$\angle POQ$ and $\angle POR$ form a linear pair of angles.
$\angle POQ + \angle POR = 180^\circ$
$(7k)^\circ + (2k)^\circ = 180^\circ$
$(9k)^\circ = 180^\circ$
$k = 20$
Frequently Asked Questions on Linear Pair of Angles
How many angles are there in a linear pair?
Only two angles can be found in a linear pair.
Are linear pairs of angles congruent?
Linear pairs of angles are not congruent. When the measure of each of the angles in a linear pair is $90^\circ$, a linear pair of angles are congruent.
Are the linear pair of angles always supplementary?
Supplementary is one of the necessary conditions for angles to be a linear pair. Hence, linear pairs are always supplementary. A linear pair forms a straight angle that measures $180^\circ$.
What is the difference between a linear pair of angles and complementary angles?
A linear pair are two adjacent angles that sum to $180^\circ$. On the other hand, complementary angles are the angles that sum up to $90^\circ$. Complementary angles need not be adjacent.
What is the difference between a linear pair of angles and vertical angles?
A linear pair are two adjacent angles that sum to $180^\circ$. They share a common vertex and a common arm.
Vertical angles are the angles that are opposite angles formed when two lines intersect each other. They only share a common vertex. Vertical angles are always congruent.
































