What Is the nth Term of an AP?
The nth term of an AP is the term that occupies the nth position from the beginning (left side) of an A.P. sequence. It’s a way to identify a specific term in the A.P. sequence based on its position.
Suppose you have a sequence of numbers that increase by the same amount each time. This kind of arithmetic sequence is called an Arithmetic Progression (AP).
Example 1: Consider the sequence 2, 5, 8, 11, 14, …
Here, the first term of this AP is T1 = 2, the second term is T2 = 5, the third term is T3 = 8, and so on. Each number in this series is more than the previous one by 3. Here, 3 is called the “common difference” because the same difference between any two consecutive terms is constant.
Example 2: In the given sequence, the first term is -6. The common difference is 7.

Recommended Games
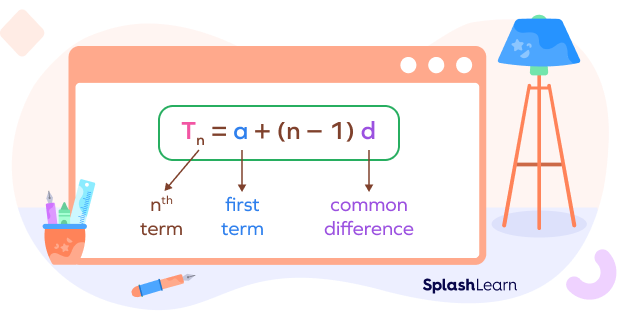
The nth Term of an AP Formula
The nth term of an AP is obtained by adding the common difference (d) multiplied by (n-1) to the first term (a) of the progression.
The nth term of an arithmetic progression (AP) can be calculated using the following formula:
| Tn= a+(n – 1)d |
where:
Tn is the nth term of the AP
a is the first term of the AP
n indicates the position of the term
d is the common difference between consecutive terms of the AP.
Recommended Worksheets
What Is the Importance of the nth Term of an AP Formula?
If you want to find the 6th number in this sequence without counting all the previous numbers, instead of repeatedly adding 3, you can use the “nth term of the AP formula.
It is not practical to keep counting one at a time, especially if we’re searching for a term far down the sequence, like the 25th term for the 100th term.
The formula lets us figure out any term in the sequence without having to count all the previous ones. It works by taking the first term and adding the common difference multiplied by (n – 1). This way, we can jump straight to the term we’re interested in without doing all the intermediate steps.
Derivation of the nth Term of an AP
An arithmetic progression (A.P) is a sequence of numbers where each term is obtained by adding a fixed amount, known as the common difference, to the preceding term.
Consider the A.P. given by
a, a+d, a+2d, a+3d,…
1st term = T1 = a
2nd term = T2 = a+d =a+(2-1)d
3rd term = T3=a+2d=a+(3-1)d
4th term = T4=a+3d=a+ (4-1)d
.
.
.
nth term Tn=a+(n-1)d
This formula represents the value of the nth term in AP whose first term is a and the common difference is d.
How to Find the nth Term of an AP
Let’s understand the steps to find the nth term of an Arithmetic Progression (AP) with the help of an example.
Formula: nth term Tn=a+(n-1)d
Example: Find the 10th term of the arithmetic progression 3, 8, 13, 18,…
Here, first term (a1) = 3
common difference (d) = 4
n = 10
Formula: Tn= a + (n – 1)d
T10= 3+(10-1)4
T10= 3+(10-1)4
T10= 3+(9)4
T10= 3+36
T10 = 39
Thus, the 10th term of the sequence is 39.
Facts about the nth Term of an AP Formula
- The common difference (d) remains constant throughout the entire arithmetic progression. It’s the fixed amount that each term increases or decreases by.
- The first term (a1) of the AP is the value at the first position, i.e., a1=a1+(1-1)d, which simplifies to a1.
- The nth term represents the value of the term at the nth position in the sequence. It’s the term that’s n steps away from the first term.
- The formula works for negative terms as well. If the common difference is negative, adding it will cause the terms to decrease as you move along the sequence.
- The formula can also be used to find terms with non-integer values. As long as the common difference and initial term are real numbers, the formula remains valid.
Conclusion
In this article, we learned about finding the nth term of an arithmetic progression (AP). This formula lets you find any term in an arithmetic progression without having to add the common difference again and again. It’s super useful when you’re dealing with large sequences and want to find terms quickly! Let’s solve a few examples and MCQs for effective practice.
Solved Examples on the nth Term of an AP
Example 1: Find the 10th term of the arithmetic progression: 5, 9, 13, 17, …
Solution:
First term (a1) = 5
common difference (d) = 4
n = 10
Tn = a + (n – 1)d
T10= 5+(10-1)4
T10= 5+(9)4
T10= 5+36 = 41
Thus, the 10th term of the sequence is 41.
Example 2: Find the 15th term of the arithmetic progression: 2, 7, 12, 17, …
Solution:
First term (a1) = 2
common difference (d) = 5
n = 15
Tn= a + (n – 1)d
T15= 2+(15-1)5
T15= 2+(14)5
T15= 2+70 = 72
Thus, the 15th term of the sequence is 72.
Example 3: What is the position of 120 in the given AP?
5, 10, 15, 20,…,120,…
Solution:
First term = a = 5
Common difference (d) = 5.
Tn = 120
We will find the value of n.
Tn= a + (n – 1)d
120 = 5 + (n – 1) 5
120 = 5 + 5n – 5
120 = 5n
n = 1205
n = 24
120 is the 24th term of the given AP.
Example 4: Find the 15th term of an AP whose 8th term is 27 and the common difference is 4.
Solution:
T8 = 27
d = 4
Formula: Tn = a + (n – 1)d
T8 = a + (8 – 1)(4)
27 = a + 28
a = 27-28
a = -1
Let’s find the 15th term.
T15 = a + (15 – 1) d
T15 = -1 + (14) 4
T15 = -1+56
T15 = 55
Thus, the 15th term of the AP is 55
Practice Problems on the nth Term of an AP
Nth Term of AP - Definition, Formula, Examples, FAQs
What is the formula for the nth term of an arithmetic progression (AP)?
The nth term of an arithmetic progression (AP) can be calculated using the formula$T_{n} = a1 + (n - 1)d$, where $a_{1}$ is the first term, d is the common difference, and n is the term number.
What does n represent in the nth term formula of an AP?
n represents the position of the term in the sequence. It helps determine which term's value is being calculated using the formula.
What is the nth term of an AP if the first term is 12 and the common difference is 0?
When the common difference is 0, it means that the terms in the sequence are all the same. In this case, the nth term formula simplifies to $T_{n} = a = 12$.
What information is NOT required to determine the nth term of an arithmetic progression (AP)?
To determine the nth term of an AP, you need the value of the first term, the common difference, and the term number (position). The value of the last term is not necessary to calculate the nth term.
If a = 10 and d = 10, then the first four terms will be:
$a = 10, d = 10, a_{1} = a = 10$
$a_{2} = a_{1} + d = 10 + 10 = 20$
$a_{3} = a_{2} + d = 20 + 10 = 30$
$a_{4} = a_{3} + d = 30+10 = 40$
Frequently Asked Questions about the nth Term of an AP
What is the nth term of an arithmetic progression?
The nth term of an arithmetic progression is the value of the term that occupies the nth position in the sequence.
Can the nth term of an AP be a negative number?
Yes, the nth term can be a negative number if the common difference (d) is negative. The formula accounts for both positive and negative terms.
Do I always need to know the previous terms to find the nth term in an AP?
No, you don’t need to know the previous terms to find the nth term using the formula. The formula directly calculates the term at a specific position based on the first term and the common difference.
Can I use the nth term formula for non-integer terms?
Yes, the nth term formula is applicable for both integer and non-integer terms. As long as the first term and the common difference are real numbers, the formula remains valid.
Is the nth term formula the same for all arithmetic progressions?
Yes, the formula Tn= a1 + (n – 1)d is applicable to all arithmetic progressions, regardless of the values of the first term and common difference. It’s a universal formula.
Is the nth term formula used only in mathematics?
No, the concept of the nth term and the formula have practical applications in various fields, including physics, finance, computer science, and more. It helps model situations where values change in a consistent manner.
How do you find the value of n in AP?
To determine the nth term of an arithmetic progression (AP), start by identifying the first term as “a” and the common difference as “d.” Decide on the term number, “n,” for which you want to find the value. Then, use the formula, Tn= a1 + (n – 1)d, where Tn represents the nth term, “a” is the first term, “d” is the common difference, and here “n” is the term number.




































