Integers

What Are Integers?

An integer is a Latin word that means “whole” or “intact.” Hence, integers include all whole numbers and negative numbers without fractions and decimals.

Let’s discuss the definition, types, and properties of integers and conduct arithmetic operations!

Integers Definition

We can define integers as numbers that can be written without a fractional component. They can be positive, negative, or zero.

Is -1 an integer? Yes!

Is -2 an integer? Yes!

Is $\frac{-1}{6}$ an integer? No!

Integer examples: $-7$, $-1$, 0, 2, 7, 15, etc.

Non-integer examples:  $\frac{8}{5}, 3.14,\sqrt{7}$, etc.

Integer symbol: The set of integers is represented by the symbol ℤ.

Types of Integers

Integer numbers can be divided into three categories: zero, positive integers, and negative integers.

Zero: Zero is an integer that is neither positive nor negative. It is simply written as 0 without any positive or negative sign.

Positive Integers: Positive integers are natural counting numbers greater than zero. They are sometimes denoted by $Z+$. Examples of positive integers are 1, 2, 3, 4, 5, 6, 7, . . .

Negative Integers: Negative integers are integers with a value less than zero. They are represented by $Z-$. Examples of negative integers are -1, -2, -3, -4, -5, -6, . . .

How to Represent Integers on a Number Line?

All three categories of integers can be visually represented on an integer number line.

Zero is placed at the center of the number line. All positive integers lie on the right side of zero, and all negative integers lie on the left side of zero.

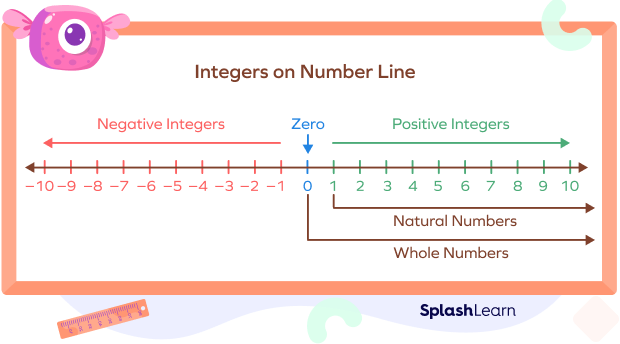
The numbers get bigger as we move from left to right on the number line. Therefore, the integer on the right-hand side is greater than the integer on the left-hand side. For example, $+6$ is greater than $-6$.

The more the integer is positive, the greater it is. For example, $+15$ is greater than $+12$.

The more the integer is negative, the smaller it is. For example, $-33$ is smaller than $-19$.

All positive integers are greater than all the negative integers. For example, $+17$ is greater than $-20$

How to Perform Arithmetic Operations on Integers

 The four basic mathematical operations are:

• Addition
• Subtraction
• Multiplication
• Division

Addition of Integers

For adding integers with the same sign, we simply add the absolute values of the numbers. The absolute value of a number is the non-negative value of the number without regard to its sign. For instance, the absolute value of $–3$ is | $–3$ |$= 3$.

The resultant integer will have the same sign as the given integers.

For example:

• $7 + 3 = 10$

Here, 7 and 3 are positive. So, the answer is +10 or simply 10.

• $(–7) + (–3) = –10$

Here, the absolute values are 7 and 3. Their sum is 10.  Since both the numbers have a (–) sign, the answer is  –10.

For adding integers with different signs, we subtract the absolute value of the integers. The resultant integer should be given the sign of the number that has the largest absolute value.

For example:

• $–4 + 8 = +4$

Here, the absolute values of integers are 4 and 8. On subtracting them, we get 4. Now eight has the largest absolute value, and its sign is $(+)$. So the answer is $+4$.

• $–6 + 2 = –$$4$

Here, the absolute values of integers are 6 and 2. On subtracting them, we get 4. Now six has the largest absolute value, and its sign is $(–)$. So the answer is $–4$.

The rules for addition are summarized in the table below:

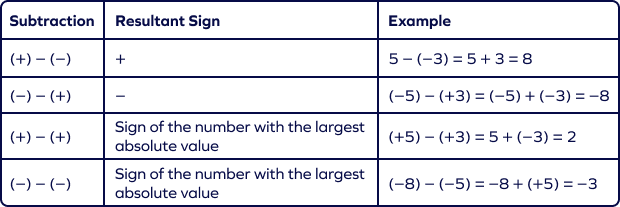
Subtraction of Integers

• Convert the subtraction operation into an addition operation by changing the sign of the second number that is being subtracted.
• Apply the rules for adding integers as discussed above to get the answer.

For example:

• $(–$$6)$ $–$ $(+7) = (–$$6) + ($$–$$7) = –$$13$

Here, we first convert the problem into addition by changing the sign of 7. Then, we follow the rules for addition. The absolute value of the integers is 6 and 7, and their sum is 13. Since both of them have a (–) sign, the answer is $–13$.

• $(+5)$ $–$ $(–$$4) = (+5) + (+4) = +9$

Here, we first convert the problem into addition by changing the sign of 4. Then, we follow the rules for addition. The absolute value of the integers is 5 and 4, and their sum is 9. Since both of them have a (+) sign, the answer is +9.

Multiplication of Integers

• If both integers have the same sign, the resultant product will have a positive (+) sign.
• If the integers have different signs, the resultant product will have a negative (–) sign.

The rules are summarized in the table below:

Division of Integers

• If both integers have the same sign, the result will have a positive $(+)$ sign.
• If the integers have different signs, the result will have a negative $(–)$ sign.

Alt Tag: Division of Integers

Properties of Integers

1. Closure Property
2. Commutative Property
3. Associative Property
4. Distributive Property
5. Additive Inverse Property
6. Multiplicative Inverse Property
7. Identity Property

Let’s learn more about them!

1. Closure Property

The closure property states that the addition, subtraction, or multiplication of integers results in an integer. So, for any two integers a and b:

• $a + b =$ Integer
• $a$ $–$ $b =$ Integer
• $a \times b =$ Integer

For example:

• $–5 + 4 = –1$
• $8$ $–$ $5 = 3$
• $2 \times 3 = 6$

However, the closure property does not work for the division of integers because the division of two integers may result in a non-integer.

For example:  $15 \div 2 = 7.5$

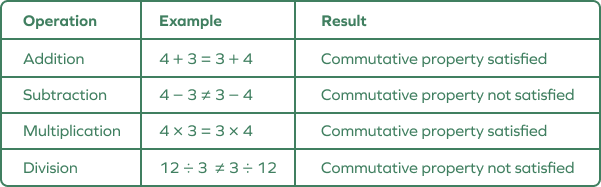
2. Commutative Property 

The commutative property states that changing the position of integers during addition and multiplication does not change the result of the operation.

Interestingly, this property is true only for addition and multiplication and not for division and subtraction.

So, for two integers a and b:

• $a + b = b + a$
• $a \times b = b \times a$

Example:

• $–5 + 2 = 2 + (–$$5) = -$$3$
• $3 \times 6 = 6 \times 3 = 18$

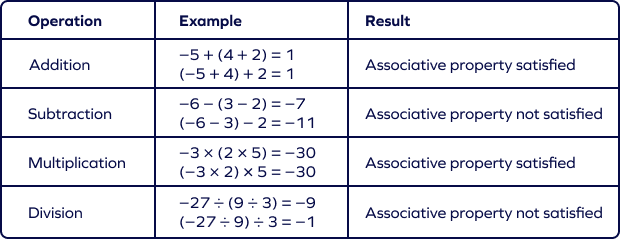
3. Associative Property

According to the associative property, changing the grouping of integers does not change the result of the operation. As above, this property is true for the addition and multiplication but not for division and subtraction.

So, for any three integers a, b, and c:

• $a + (b + c) = (a + b) + c$
• $a \times (b \times c) = (a \times b) \times c$

For example:

4. Distributive Property 

The distributive property states that the multiplication of integers can be distributed over addition and subtraction to make the calculation easier.

So, for three integers a, b, and c:

$a \times (b + c) = (a \times b) + (a \times c)$

For example:

• $5 \times (4 + 3) = (5 \times 4 + 5 \times 3) = 35$
• $–2 \times (6 + 1) = \left\{(–2) \times 6 + (–2) \times 1\right\} = –14$

5. Additive Inverse Property

This property states that the addition of an integer and its negative value will always be zero. So, for any integer a:

$a + (–$$a) = 0$

For example:

• $6 + (–$$6) = 0$
• $15 + (–$$15) = 0$

6. Multiplicative Inverse Property

This property states that the multiplication of an integer and its reciprocal will give the answer 1.

So, for any integer a:

$a \times \frac{1}{a} = 1$

For example:

• $3 \times \frac{1}{3} =1$
• $–15 \times \frac{1-}{15} = 1$

7. Identity Property 

The identity property of an integer states that any integer added to zero will result in the same integer. Similarly, any integer multiplied by one will give the same integer.

So, for any integer a:

• $a + 0 = 0 + a = a$
• $a \times 1 = 1 \times a = a$

Example:

• $10 + 0 = 0 + 10 = 10$
• $10 \times 1 = 1 \times 10 = 10$

Conclusion

So, we’ve covered everything from the definition and properties of integers and how to perform mathematical operations on them. The more you practice, the better you’ll understand integer numbers. Good luck!

Solved Examples on Integers

1. Sort the numbers as integers and non-integers.

–5, 7.5, 100, $\frac{3}{7}$, $–4.25$, 0

Solution:

Integers $= –$$5$, 100, 0

Non-integers $= 7.5$, $\frac{3}{7}$, $–4.25$

Integer numbers do not include fractions and decimals. Hence, $–5$, $100$, and 0 are integer numbers, but 7.5, $\frac{3}{7}$, and $–4.25$ are not.

2. Solve: $(–$$8) –$ $(–$$5)$

Solution:

Step 1: First, we change the operation to an addition operation by changing the sign of the number to be subtracted.

So, (–8) – (–5) = –8 + 5

Step 2: Then we follow the addition operation

Since the signs are different, we need to find the difference in their absolute value.

So, $8$ $–$ $5 = 3$

The sign of the resultant integer will be the sign of the integer with the highest absolute value.

Here, 8 is the integer with the highest absolute value, and its sign is negative.

So the answer is $–3$.

3. Using the number line, find the integer which is:

• 6 more than 3
• 7 less than 4

Solution:

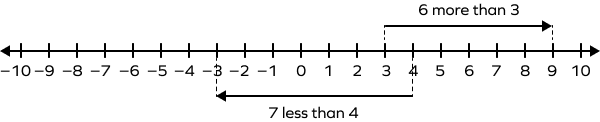
We know that the numbers get larger as we move from left to right. So, to find the number that is 6 more than 3, we have to move six steps to the right from 3. That will give us the answer 9.

Again, to find the number that is 7 less than 4, we have to move 7 steps to the left from 4. That will give us the answer $–3$.

Practice Problems on Integers

Frequently Asked Questions

Related Article Links

• Whole Numbers
• Natural Numbers
• Number System