What Is Pentagram in Math?
A pentagram is a star-shaped polygon with five points. It is also known as a “star pentagon.”
A pentagram consists of a pentagon at the center.
Definition of Pentagram
In mathematics, a pentagram is a five-pointed star-shaped polygon formed by connecting five non-collinear points with line segments.
Vertices, edges, and angles in a pentagram:
Number of Vertices: 5
Number of Edges: 5
Number of Angles: 5 (Each vertex forms one angle)
Types of Pentagram
Based on the geometric shape and symmetry of the pentagram, it can be categorized into two distinct forms:
- Regular pentagram
- Irregular pentagram
Regular Pentagram
A regular pentagram comprises five congruent isosceles triangles that form the five points, with a regular pentagon at its center. In regular pentagrams, all sides and angles are equal. It is a pentagram with balanced symmetry.

Irregular Pentagram
In an irregular pentagram, the triangles forming the five points are not all congruent, resulting in the center pentagon also being irregular. The sides and angles are not equal, thus not meeting the criteria of a regular pentagram.

Angles in a Regular Pentagram
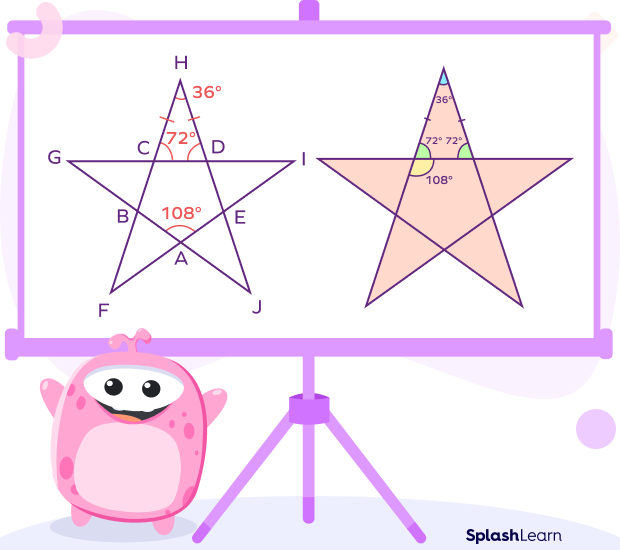
Angles of the Regular Pentagon
As previously mentioned, a regular pentagram encloses a regular pentagon within it. Therefore, each interior angle of this inner pentagon measures 108º.
For the regular pentagon ABCDE, each interior angle measures 108°.
Supplementary Angles
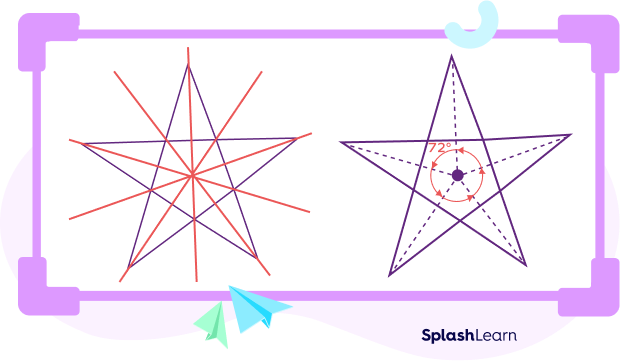
Since the five triangles forming pentagram FGHIJ are isosceles, their base angles are congruent, thus angle HDC = 72°.
Supplementary angles add up to 180°.
In a pentagon, the side acts as the base for an isosceles triangle, resulting in base angles of 72° each, along with an apex angle of 36°. As there are five sides in a pentagon, there are ten angles measuring 72° each.
Considering ∠BCD = 108°, its supplement, ∠HCD = 72°.
Interior Angles of Regular Pentagram
In a regular pentagram, the angles at each of the five points have equal measures of 36°.
The apex angle of the isosceles triangle will be the interior angle of the regular pentagram. These angles are 36° each. As there are five-pointed ends or apex, there are five 36° angles.
Applying the sum of interior angles in a triangle (180°), we get
∠H = 180° – (72° + 72°) = 36°.
The same applies to angles F, G, J, and I, each measuring 36° as well.
How to Construct a Regular Pentagram
- Draw the 5 diagonals of a regular pentagon to create a regular pentagram. Two distinct diagonals can be drawn from any vertex of a regular pentagon.
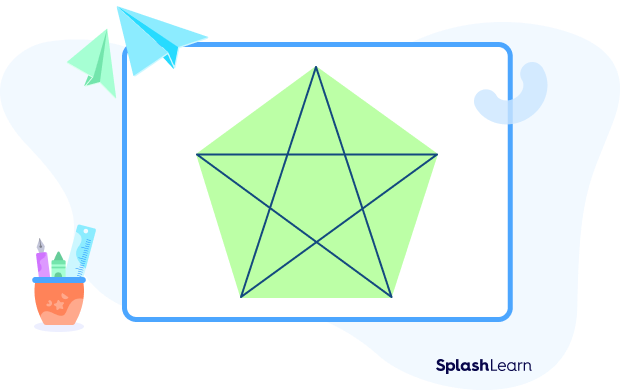
- Extending the sides of a regular pentagon also forms a pentagram. The five points of intersection formed by extending each side of the regular pentagon create the five points of a regular pentagram.

Symmetry in a Regular Pentagram
A regular pentagram has 5 lines of symmetry. It has a rotational symmetry of order 5. If rotated, a pentagram fits the original shape 5 times within 360°.
Facts about Pentagram
- Each regular pentagram comprises five congruent isosceles triangles.
- Some pentagram-shaped culinary items include star anise, pastry and cake decorations and star fruit.
Conclusion
In this article, we learned about the pentagram—a captivating five-pointed star-shaped polygon with unique properties. Let’s explore some examples and practice MCQs to deepen our understanding.
Solved Examples on Pentagram
Example 1: State the difference between pentagram and pentagon.
Solution:
Pentagram vs. pentagon:
- A pentagram is a five-pointed star-shaped polygon, while a pentagon is a five-sided polygon with straight sides.
- In a pentagram, the lines extend outward, creating a star-like appearance, whereas a pentagon has its sides connected, forming a closed shape with five sides.
Example 2: What are properties of a pentagram?
Solution:
- Five-Pointed Star: Pentagram is a star-shaped polygon with five points (five corners or tips of the star).
- Five Intersecting Lines: The lines in a pentagram extend outwards from its points, creating five intersecting lines.
- Symmetry: A regular pentagram has 5 lines of symmetry, dividing it into five congruent sections.
- Rotational Symmetry: It has a rotational symmetry of order 5, meaning it can be rotated five times to match its original shape.
- Pentagrams can be regular (all sides and angles equal) or irregular (sides and angles unequal).
Example 3: What are angles in a regular pentagram?
Solution:
Each interior angle of the inner pentagon measures 108º.
Each apex angle of a regular pentagon is 36°.
Base angles of five isosceles triangles are 72°.
Practice Problems on Pentagram
Pentagram in Math - Definition, Types, Angles, Examples, FAQs
What type of pentagon is formed in the center of a regular pentagram?
A regular pentagram encloses a regular pentagon within it.
How many lines of symmetry does a regular pentagram have?
A regular pentagram shape has 5 lines of symmetry.
What is the rotational symmetry order of a pentagram?
The order of rotational symmetry in a regular pentagram is 5.
Frequently Asked Questions about Pentagram
Are all pentagrams regular?
No, pentagrams can be either regular or irregular.
What does a regular pentagram consist of?
A regular pentagram consists of 5 congruent isosceles triangles forming the 5 points, with a regular pentagon in its center.
How can I construct a regular pentagram?
A regular pentagram can be constructed by drawing 2 diagonals from each vertex of a regular pentagon.
Can you explain the difference between convex and concave pentagrams?
Convex pentagrams have all internal angles less than 180 degrees, while concave pentagrams have at least one angle greater than 180 degrees.
















