What Is a Perfect Square Trinomial?
A perfect square trinomial is a polynomial that can be written as a perfect square of a binomial.
Perfect square trinomials are algebraic polynomials that can be factored into the square of a binomial. They have a specific form and exhibit some distinct properties.
Perfect square trinomial example:
x2 + 6x + 9 is a perfect square trinomial expression, since it can be factored as (x + 3)2, the square of the binomial (x + 3).
(x + 3)2 = x2 + 6x + 9
NOTE:
- Trinomials are polynomials consisting of three terms.
- Binomials are polynomials consisting of two terms.
Recommended Games
Perfect Square Trinomial: Definition
A perfect square trinomial is a polynomial that can be expressed as the square of a binomial. It is an expression of the form (ax)2 + 2abx + b2 or (ax)2 – 2abx + b2.
where a and b are real constants, $a \neq 0$.
Recommended Worksheets
Properties of a Perfect Square Trinomial
- The first term is a perfect square.
- The last term is a perfect square.
- The middle term of the perfect square trinomial is twice the product of the square roots of the first and last terms.
- A perfect square trinomial is a special type of quadratic expression formed when a binomial is multiplied to itself.
Perfect Square Trinomial Formula
We already know that a perfect square trinomial may be factored into the square of a binomial. It means that it is in the following form:
(ax + b)2 = (ax)2 + 2abx + b2
(ax – b)2 = (ax)2 – 2abx + b2
where a and b are real constants, $a \neq 0$.

Example: Multiply the binomial (2y + 5) with itself.w
(2y + 5) $\times$ (2y + 5) = (2y + 5)2
We can use this formula to expand it to a perfect square trinomial as under
(2y + 5)2 = (2y)2 + 2(2y)(5) + 52
(2y + 5)2 = 4y2 + 20y + 25
How to Find a Perfect Square Trinomial
To determine if a trinomial is a perfect square trinomial, you can compare the given trinomial with the form (ax)2 + 2abx + b2 or (ax)2 – 2abx + b2.
If it matches the form, it is a perfect square trinomial.
Step 1: See whether the first term is a perfect square or not.
Step 2: See whether the last term is a perfect square or not.
Step 3: See if the middle term is twice the product of the square roots of the first and last terms.
Example: x2 + 6x + 9
First term: x2 is a perfect square of x.
Last term: 9 is a perfect square of 3.
Middle term: 6x.
6x is twice the product of x and 3.
2(x)(3) = 6x
Therefore, the trinomial x2 + 6x + 9 is a perfect square trinomial. It is the square of the binomial (x+3).
(x + 3)2 = x2 + 6x + 9
How to Factor a Perfect Square Trinomial
Let’s understand the steps to factor a perfect square trinomial of the form (ax)2 + 2abx + b2 or (ax)2 – 2abx + b2.
Step 1: Find the square roots of the first term and the last term. These square roots represent the terms of the binomials.
Here, the roots are (ax) and b.
Step 2: Check the sign of the middle term. If the original trinomial has a positive middle term, write the factored form as (ax + b)2.
If the original trinomial has a negative middle term, write the factored form as (ax-b)2.
Example 1: Factor x2 + 6x + 9.
x2 = xx
9 = 3$\times$3 = 32
The middle term is positive. Thus, the sign of the binomial will be positive.
x2 + 6x + 9 = (x + 3)2
Example 2: 9x2 – 12x + 4
First term = 9x2 = (3x)2
Last term = 4 = (2)2
Middle term has a negative sign.
Middle term = 12x = 2 $\times$ 3x $\times$ 2
Thus, 9x2 – 12x + 4 = (3x – 2)2
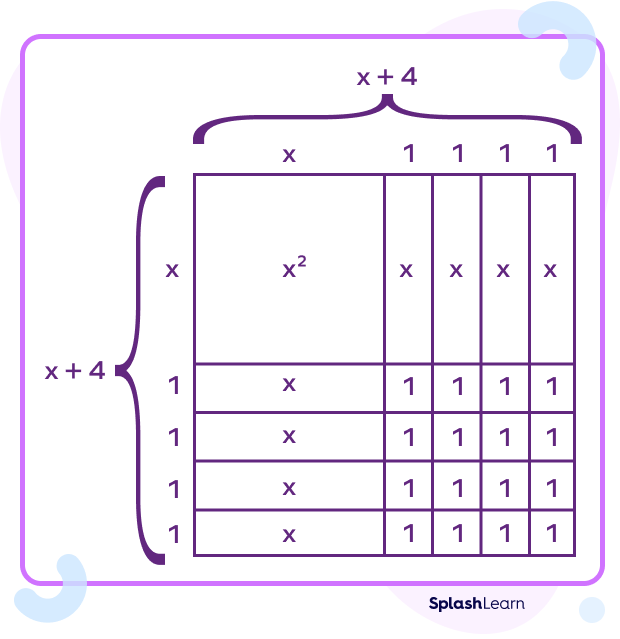
Visualizing Perfect Square Trinomials
We can understand perfect square trinomials and how to factor them using area models.
Observe the big square.
Area of the big square represents the perfect square trinomial. It is composed of one square with area x2 square units, 8 rectangles with area x square unit each, and 16 squares with area 1 square unit each.
(x + 4)2 = x2 + 8x + 16
Facts about Perfect Square Trinomials
- A quadratic expression obtained from the square of a binomial equation is a perfect square trinomial.
- If a trinomial is in the form ax2 + bx + c is said to be a perfect square, if and only if it satisfies the condition b2 = 4ac.
Conclusion
In this article, we learned about the perfect square trinomials, their properties, how to solve a perfect square trinomial and the formulas. Let’s solve a few examples and MCQs for better understanding.
Solved Examples on Perfect Square Trinomials
1. Factorize the perfect square trinomial 4x2 + 12x + 9.
Solution:
Perfect square trinomial: 4x2 + 12x + 9
First term = 4x2 = (2x)2
Last term = 9 = (3)2
Middle term has a positive sign.
Compare the given perfect square trinomial with (ax + b)2 = (ax)2 + 2abx + b2.
Here, a = 2x and b = 3
(2x + 3)2 = 4x2 + 12x + 9
2. Is the trinomial 3x2 + 8x + 4 a perfect square trinomial?
Solution:
Given trinomial: 3x2 + 8x + 4
First term = 3x2 = $(\sqrt{3x})^{2}$
Last term = 4 = (2)2
Middle term = 8x
Compare the given trinomial with (ax + b)2 = (ax)2 + 2abx + b2.
It does not match the form.
The middle term is not twice the product of the roots 2 and 8x.
Therefore, the given expression cannot be factored as the square of a binomial. It is not a perfect square trinomial.
3. Find the factors of the perfect square trinomial 16a2 – 40ab + 25b2.
Solution:
Given expression: 16a2 – 40ab + 25b2
First term = 16a2 = (4a)2
Last term = 25b2 = (5b)2
The sign of the middle term is negative. So, the factors will be of the form (4a-5b).
40ab = 2(4a)(5b)
Compare the given perfect square trinomial with (ax + b)2 = (ax)2 + 2abx + b2
16a2 – 40ab + 25b2 = (4a – 5b)(4a – 5b)
Practice Problems on Perfect Square Trinomials
Perfect Square Trinomial - Definition, Formula, Examples, FAQs
Which of the following expressions is a perfect square trinomial?
$x^{2} + 6x + 9 = (x + 3)^{2}$
What is the factored form of the perfect square trinomial $x^{2} + 10x + 25$?
$x^{2} + 10x + 25 = x^{2} + 10x + 5^{2} = (x + 5)^{2}$
A perfect square trinomial is the product of a _______ with itself.
A perfect square trinomial is the product of a binomial with itself.
Frequently Asked Questions about Perfect Square Trinomials
Where are perfect square trinomials used?
Perfect square trinomials are used in algebra as they let us easily factor and solve quadratic equations.
How to solve a quadratic equation that is a perfect square trinomial?
In a quadratic equation which is a perfect square trinomial, we have to take the square root of both sides and then solve for the variable (x). If applicable, remember to take into account both the positive and negative square roots.
What is the importance of identifying perfect square trinomials?
Recognizing perfect square trinomials helps in the simplification of expressions, factorization, and solving of equations in a more efficient manner.
What is the method of completing squares?
The method of completing a square is a process that involves manipulating the quadratic expression to create a perfect square trinomial. It is extremely useful in simplifying and solving quadratic equations.
How many factors are there in a perfect square trinomial?
A perfect square trinomial has a binomial factor that is repeated twice.
What makes a perfect square trinomial?
The square of any binomial results in a perfect square trinomial.



























