What Is Roster Notation or Roster Form of a Set?
Roster notation or the roster form of a set is represented using curly brackets with elements separated by comma.
Here, the order of elements does not matter. This is a simple and straightforward way to represent a set by listing the elements within curly brackets.
Roster Notation Example: The set of natural numbers less than 10 can be written using roster form as
$A = \left\{1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8,\; 9\right\}$
In mathematics, a set is defined as a collection of distinct, well-defined objects. Each item in the set is known as an element of the set. We always write elements of a set within curly brackets. A set can be presented into two ways:
- Roster Notation
- Set Builder Form
In this article, we will learn about the Roster Notation.
Recommended Games
Venn Diagram for Roster Form
Roster form is the most simple method for representing the elements of a set. In the roster form, the elements are listed in a row.
Drawing a Venn diagram with the help of roster notation is easy since we can easily read the elements and understand the number of elements present. Similarly, writing a set in the roster form using a given Venn diagram is equally not at all difficult.
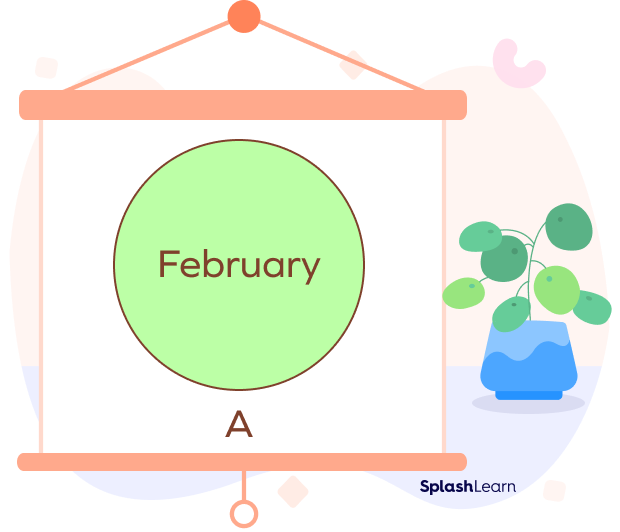
Example 1: Let A be the set of months starting with F.
Thus, A contains a single element. In roster form, the set A can be represented as
$A = \left\{February\right\}$
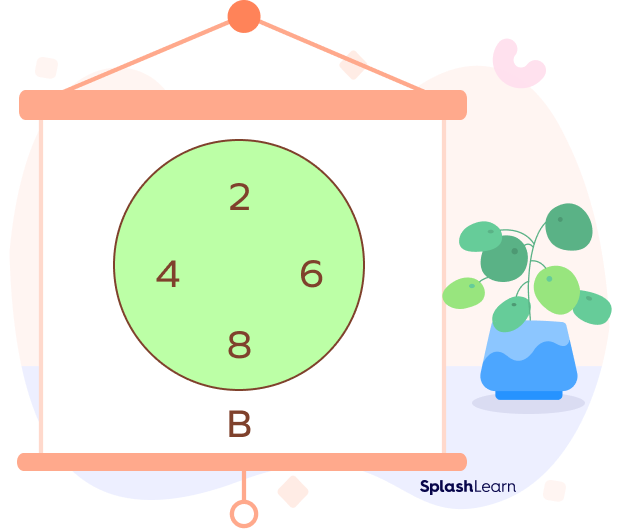
Example 2: Let B be the set of even numbers between 0 and 10.
Set B can be represented in roster form as
$B = \left\{2,\; 4,\; 6,\; 8\right\}$
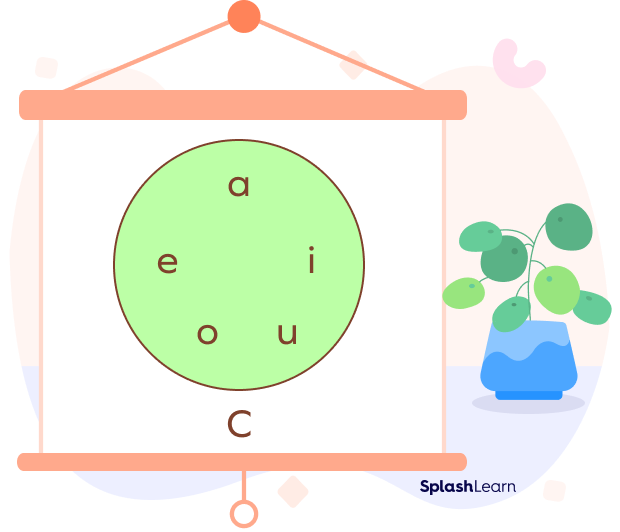
Example 3: Suppose we have a Venn diagram of set C.
We can define the set using the Roster notation as
$C = \left\{a,\; e,\; i,\; o u\right\}$
Limitations of Roster Notation
In the roster notation, we list the elements within curly brackets and separate the elements by comma. Now, imagine listing a large number of elements. It will be time consuming. It will also be difficult to get the idea of what the set actually represents.
Example: Suppose we want to represent the first 1000 natural numbers in a set A. It is not convenient to write 1000 numbers in a single row. We can overcome this limitation by using an ellipsis or three periods (…), which indicates that the same pattern is continued.
Write the first few elements followed by three dots and finally the last element. Separate these elements with a comma.
$A = \left\{1,\; 2,\; 3,\; 4,…, 999\right\}$
Example 2: If a set has an infinite number of elements, like the set of whole numbers, it can be represented in roster form like:
$D = \left\{0,\; 1,\; 2,\; 3,\; 4,…\right\}$
Roster Form to Set Builder Form
We know that a set is a collection of well-defined objects. To represent a set in the set builder form, we first identify the unique property satisfied by all the elements in the given set and use a mathematical statement or a condition with a variable to define the set.
Roster form to the set builder form examples:
| Roster Form | Set Builder Form |
|---|---|
| $A = \left\{1,\; 2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8\right\}$ | $A = \left\{ x\in N | 1 \le x \le 8\right\}$ |
| $B = \left\{1,\; 4,\; 9,\; 16,\; 25,…\right\}$ | $B = \left\{ x^{2} | x \in N\right\}$ |
Roster Notation vs. Set Builder Notation
| Roster Form | Set Builder Form |
|---|---|
| It is represented by listing elements within curly brackets. Elements are separated by comma. | It uses the unique properties or conditions satisfied by all the elements of the set to define the set. |
| We actually write the elements of the set. | We do not write the actual elements of the set, but a logical condition/statement/ formula that leads to the elements of the set. |
| Convenient to use with the sets having fewer number of elements | Convenient to use with the sets having a large or an infinite number of elements |
| Easy to read and understand for a layman | Can be tricky since a lot of math operators and symbols are used. Requires knowledge of math concepts to identify the elements of the set based on a given condition |
| Example: Set of positive multiples of 6 $A = \left\{1,\; 2,\; 3,\; 6\right\}$ | Example: Set of positive multiples of 6 $A = \left\{x | x = 6n\; \text{where}\; n\in N\right\}$ |
Facts about Roster Notation
- The roster form is also known as the enumeration notation as the enumeration is the process of listing things one after another.
- The Roster method is also known as the tabular method.
Solved Examples on Roster Notation
1. Write the set of odd numbers less than 10 in a set notation form. What is the cardinality of the set?
Solution:
Set of odd numbers $= \left\{1,\; 3,\; 5,\; 7,\; 9,\; 11,\; 13,…\right\}$
Set of odd numbers less than $10 = \left\{1,\; 3,\; 5,\; 7,\; 9\right\}$
Cardinality of the set $= 5$
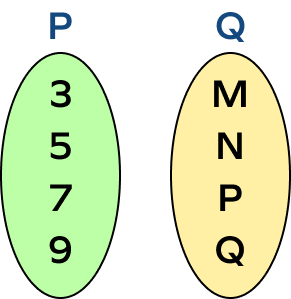
2. Express the sets P and Q in the roster form.
Solution:
In the set P, there are 4 elements. Let’s list them using the roster notation.
$P = \left\{3,\; 5,\; 7,\; 9\right\}$
In the set P, there are 4 elements. Let’s list them using the roster notation.
$Q = \left\{M,\; N,\; P,\; Q\right\}$
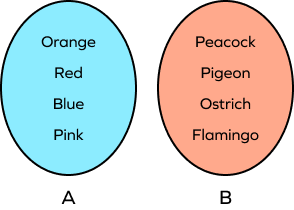
3. Draw the Venn diagram for the given sets.
$A = \left\{Orange,\; Red,\; Blue,\; Pink\right\}$
$B = \left\{Peacock,\; Pigeon,\; Ostrich,\; Flamingo\right\}$
Solution:
$A = \left\{Orange,\; Red,\; Blue,\; Pink\right\}$
$B = \left\{Peacock,\; Pigeon,\; Ostrich,\; Flamingo\right\}$
Venn diagrams:
4. Express the set $P = \left\{p : p = 2k + 1,\; 2 \lt k \lt 7\right\}$ in the roster notation.
Solution:
$p = 2k + 1$
When $k = 3,\; p = 2 \times 3 + 1 = 7$
When $k = 4,\; p = 2 \times 4 + 1 = 9$
When $k = 5,\; p = 2 \times 5 + 1 = 11$
When $k = 6,\; p = 2 \times 6 + 1 = 13$
$P = \left\{7,\; 9,\; 11,\; 13\right\}$
5. Write the given set in the roster notation to the set builder notation.
$A = \left\{1,\; 8,\; 27,\; 64,\; 125, …\right\}$
Solution:
$A = \left\{1,\; 8,\; 27,\; 64,\; 125, …\right\}$
Here, we have a set of cubes of natural numbers.
$A = \left\{x^{3}\; :\; x \in N \right\}$
Practice Problems on Roster Notation
Roster Notation (Roster Form of Set): Meaning, Examples
Identify the roster form for the set of vowels in the word MATHEMATICS.
Vowels in the word MATHEMATICS are A, E, and I.
Note that repetition is not allowed in sets.
The roster form for the first three positive multiples of 9 is
$1 \times 9 = 9$
$2 \times 9 = 18$
$3 \times 9 = 27$
$A = \left\{9,\; 18,\; 27\right\}$
The set $B = \left\{y \;:\; y = 3n^{2},\;-\;3 \le n \le 0\right\}$ can be written in the roster notation as
$-\;3 \le n \le 0$
Possible values of n are $n = \;-\;3,\;-\;2,\;-\;1,\;0$
When $n = \;–\; 3$, we have $y = 3(\;-\;3)^{2} = 27$
When $n = \;–\; 2$, we have $y = 3(\;-\;2)^{2} = 12$
When $n = \;–\; 1$, we have $y = 3(\;-\;1)^{2} = 3$
When $n = 0$, we have $y = 3(\;-\;3)^{2} = 0$ $B = \left\{27, \;12,\; 3,\; 0\right\}$
The correct roster form for the sets in the following Venn diagram is:
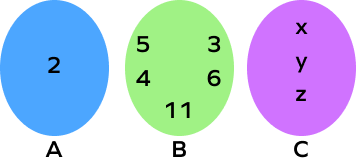
$A = \left\{2\right\}$ $B = \left\{3,\; 4,\; 5,\; 6,\; 11\right\}$ $C = \left\{x,\; y,\; z\right\}$
Frequently Asked Questions about Roster Notation
What is a singleton set?
A set having a single element is called a singleton set.
How do you represent a null set in roster form?
Null set is a set which does not have any element. The null set can be represented as {} in the roster form.
What is meant by the cardinality of the set?
The cardinality of the set is the number of the elements in the set. If the set is A, then its cardinality is represented by n(A).
What is interval notation?
Interval notation is a method of writing the subsets of the real number line. For example: $P = \left\{x : – 2 \lt x \lt 5\right\} = \left( \;–\; 2,\; 5\right)$
What is the meaning of set notation$\in$ ?
Set Notation means “belongs to.” On the other hand, ∉ means “does not belong to.”
If $A = \left\{2,\; 5,\; 8,\; 10\right\}$, then we can say that $2 \in A,\; 3 \in A,\; 5 \in A$, and $10\in A$.
However, $1 \notin A$.
What are the rules for the set roster notation?
Elements are listed in a single row within curly brackets $\left\{ \right\}$. If the set contains more than one element, the elements are separated by a comma. The order of elements is not important.

















