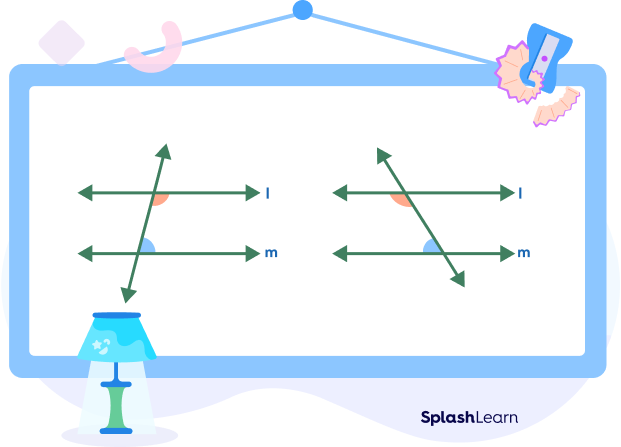
What Are the Same Side Interior Angles in Geometry?
Same side interior angles are a pair of non-adjacent angles formed by two parallel lines (or non-parallel lines) cut by a transversal. They lie on the same side of the transversal and in the interior region between two lines.
The same side interior angles are also called co-interior angles or consecutive interior angles.
The given diagram shows the same side interior angles formed when i) parallel lines are cut by a transversal ii) two non-parallel lines are cut by a transversal
Recommended Games
Same Side Interior Angles: Definition
Two non-adjacent interior angles that lie on the same side of the transversal are known as Same Side Interior Angles.
Recommended Worksheets
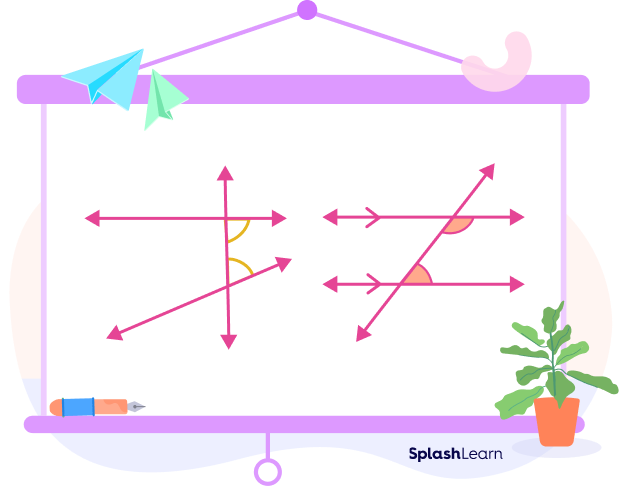
How To Spot or Identify Same Side Interior Angles
Same side interior angles form a C-shaped pattern due to their position.
Properties of Same Side Interior Angles
- They have different vertices.
- They lie on the same side of the transversal.
- They lie in the interior region formed between the two lines.
- They share a common side.
Same Side Interior Angle Theorem (Same Side Interior Angles Postulate)
Same Side Interior Angle Theorem Statement: If a transversal intersects two parallel lines, then each pair of same side interior angles are supplementary (they add up to 180°.)
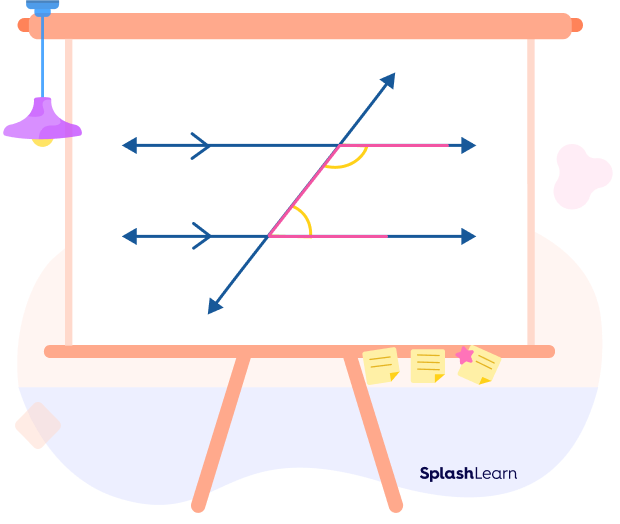
Proof of Same Side Interior Angles Theorem
Given: l || m are parallel, and n is the transversal.
To prove:
∠4 + ∠5 = 180°
∠3 + ∠6 = 180°
Proof:
∠1 = ∠5 (corresponding angles)
∠1 + ∠4 = 180° (Linear pair of angles)
On Substituting ∠1 = ∠5, we get
∠4 + ∠5 = 180°
Similarly, we can show that
∠3 +∠6 = 180°
Thus, the same side interior angles are supplementary.
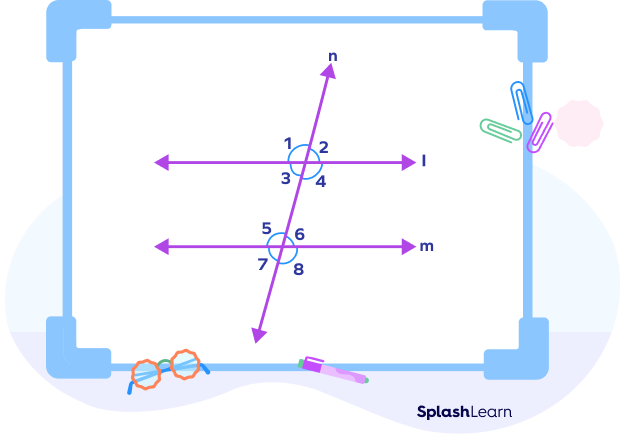
Converse of the Same Side Interior Angles Theorem
Converse of Same Side Interior Angle Theorem: If a transversal intersects two lines in a way that a pair of the same side interior angles are supplementary, then the two lines are said to be parallel.
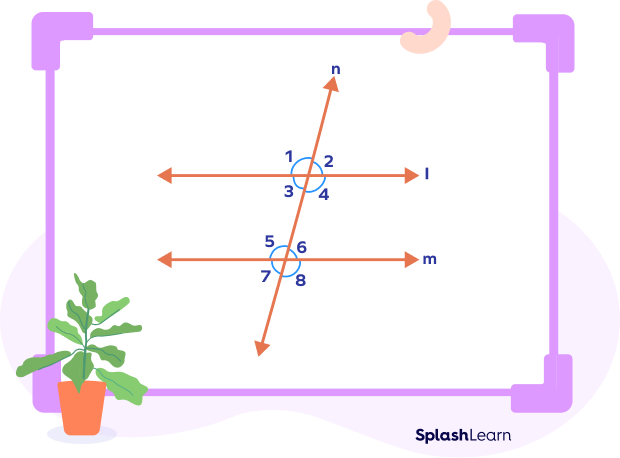
Given:
∠3 +∠6 = 180°
∠4 + ∠5 = 180°
To prove: l || m
∠5 + ∠4 = 180° (given)
∠1 + ∠4 = 180° (linear pair of angles)
On comparing, we get
∠1 + ∠4 = ∠5 + ∠4
∠1 = ∠5
∠1 and ∠5 are a pair of corresponding angles.
l is parallel to m. (Converse of corresponding angles postulate)
Same Side Interior Angles of a Parallelogram
The opposite sides of a parallelogram are parallel. So, any two adjacent angles of a parallelogram are basically the same side interior angles formed by two parallel lines and a transversal.
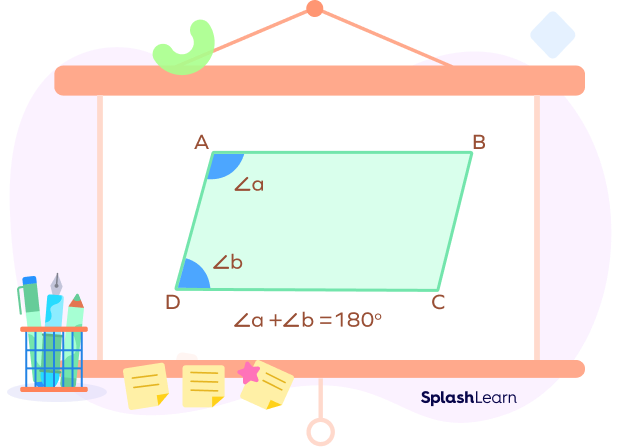
We know that same side interior angles are supplementary when lines are parallel. This gives rise to the important property in parallelograms which states that:
Two adjacent angles of a parallelogram are always supplementary.
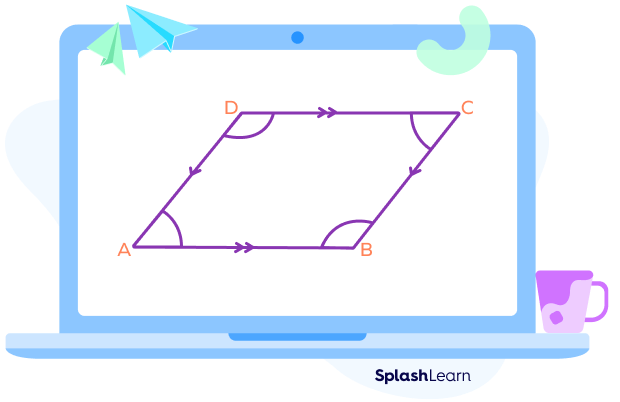
In the following parallelogram, ∠A and ∠B, ∠B and ∠C, ∠C and ∠D, and ∠D and ∠A are pairs of consecutive interior angles.
| Parallel sides | Transversal | Property |
|---|---|---|
| AB ∥ CD | BC | ∠B + ∠C = 180° |
| AB ∥ CD | AD | ∠A + ∠D = 180° |
| AD ∥ BC | CD | ∠C + ∠D = 180° |
| AD ∥ BC | AB | ∠A + ∠B = 180° |
Facts about Same Side Interior Angles
- Same-side interior angles are supplementary when the lines intersected by the transversal line are parallel.
- Same side interior angles are also known as consecutive interior angles or co-interior angles.
Conclusion
In this article, we learned about same side interior angles, which are also known as co-interior angles. We learned the important theorem based on same side interior angles that helps to determine whether two lines are parallel or not. Let’s solve a few examples for better understanding.
Solved Examples on Same Side Interior Angles
1. Is l parallel to m?
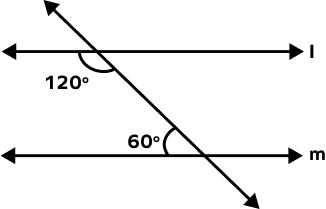
Solution:
The given pair of angles are the same side interior angles.
120° + 60° = 180°
The angles are supplementary.
Hence, l is parallel to m.
2. In the following figure, find the value of x.
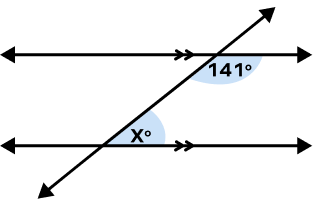
Solution:
Two parallels are cut by a transversal.
Given angles represent a pair of same side interior angles.
They must add up to 180°.
So, 141° + x = 180° (Same Side Interior Angles)
x = 180° – 141°
x = 39°
3. Find the value of x in the following figure,
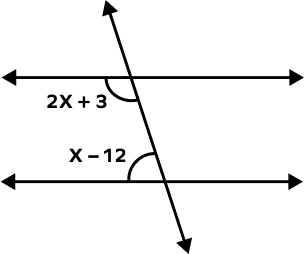
Solution:
2x + 3 + x – 12 = 180° (Same Side Interior Angles)
3x – 9 = 180°
3x = 180° + 9°
3x = 189°
$\Rightarrow x = \frac{189^{\circ}}{3} = 63^{\circ}$
4. Two parallel lines are cut by a transversal, and a pair of same side interior angles measure (3y + 6)° and (9y – 24)° respectively. Find the value of y.
Solution:
(3y + 6)° + (9y – 24)° = 180° (Same Side Interior Angles)
12y – 18° = 180°
12y = 180° + 18°
12y = 198°
y $= \frac{198^{\circ}}{12}$
y = 16.5°
Practice Problems on Same Side Interior Angles
Same Side Interior Angles - Definition, Theorem, Examples, Facts
Which of the following is the pair of Same Side Interior Angles?
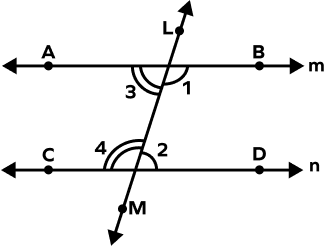
Consecutive Interior Angles are the angles which are on the same side of transversal and are on the interior part. So, ∠3 and ∠4 are same side interior angles.
Which of the following is true for the following figure?
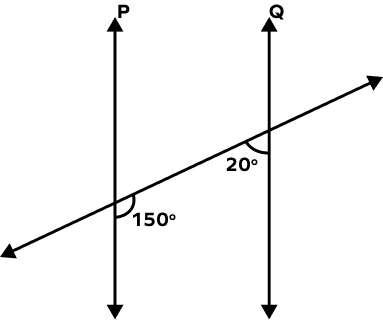
150° + 20° = 170°
Angles are not supplementary.
Hence, line P is not parallel to line Q.
If one of the same side interior angles is double the other, then what will be the value of each of the angles?
Let one consecutive interior angle be x°.
Other interior angle = 2x°
x° + 2x° = 180°
3x° = 180°
x = 60°
2x = 2 60° = 120°
For which value is each of the same side interior angles equal?
Let each consecutive interior angle be x.
x + x = 180°
2x = 180°
x $= \frac{180^{\circ}}{2} = 90^{\circ}$
What is the value of each angle in the following figure?
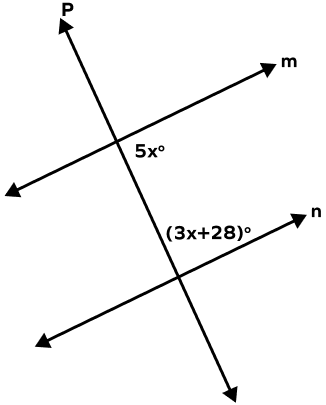
m is parallel to n and p is the transversal.
5x° + (3x+28)° = 180° (Same Side Interior Angles)
8x + 28° = 180°
8x = 180° – 28°
8x = 152°
x $= \frac{152^{\circ}}{8} = 19^{\circ}$
Angles = 5 19° = 95° and 3 19° + 28° = 57° + 28° = 85°
Frequently Asked Questions about Same Side Interior Angles
Are Same Side Interior Angles Always Supplementary?
No. Same Side Interior angles are supplementary when the lines are parallel.
What is another name for Same Side Interior Angles?
The other name for Same Side Interior angles is co interior angles or interior angles on the same side of transversal.
Are the same side interior angles congruent? When are the same side interior angles equal?
Same side interior angles formed by two parallel lines and a transversal are supplementary and not congruent. Same Side Interior angles are equal only in a rectangle.
What are the Same Side Exterior Angles?
Same side exterior angles are the angles which lie on the exterior side of the two lines and are on the opposite side of transversal. They are supplementary when lines are parallel.
How to solve the same side interior angles?
If the lines are parallel and you know one angle in the pair of same side interior angles, then you can find the other angle by subtracting the given angle from 180 degrees.




































