What Is a Segment Bisector in Geometry?
The segment bisector simply means a geometric figure that bisects a line segment. It refers to any geometric figure (a line, a point, a line segment, or a ray) that cuts a line segment precisely in two equal parts.
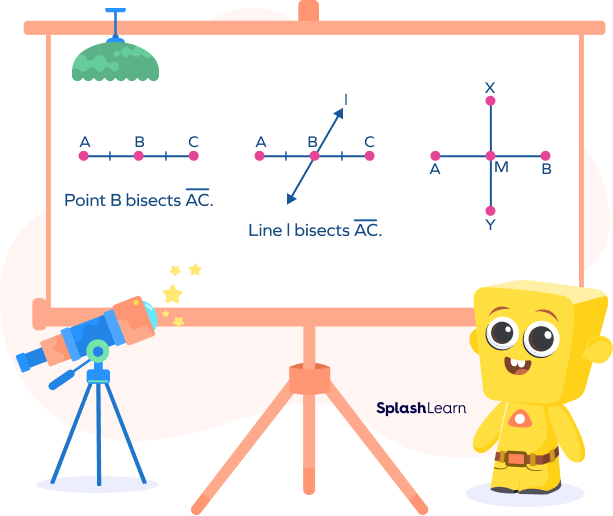
When a line segment is cut or split at its midpoint into two equal halves by any geometric figure such as a point or a line, we refer to the geometric figure as a segment bisector. The bisector of a line segment could be
- a point
- a line
- a line segment
- a ray
Recommended Games
What Is a Line Segment?
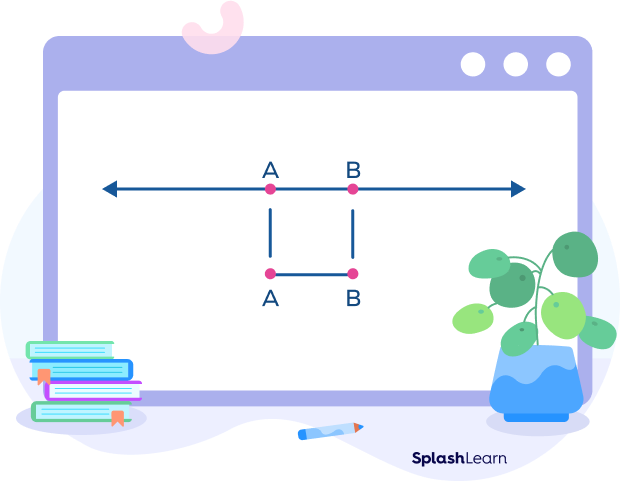
A line segment is a section or a part of a line that can connect two endpoints. A line has no endpoints and extends infinitely in both directions.
If you mark two points A and B on a line, then the section of the line joining A and B is called a line segment AB, as shown in the figure below. Thus, a line segment has two endpoints and a definite length.
Segment Bisector: Definition
A geometric figure (a point, a line, a line segment, or a ray) that cuts a line segment exactly in half is called a segment bisector.
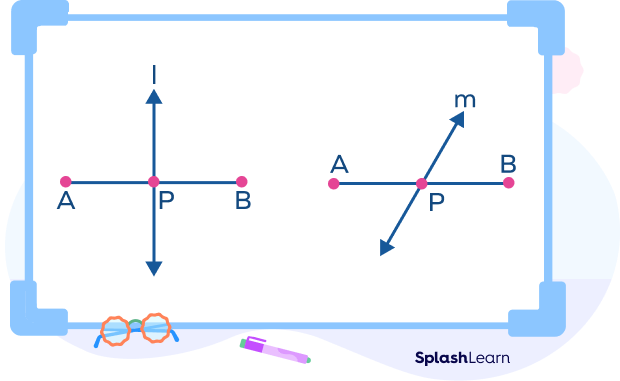
A segment bisector can be a vertical line or a slanted line.
In the above figure lines ‘l’ and ‘m’ are segment bisectors that bisect the segment AB at point P.
Thus, AP = BP.
Types of Segment Bisectors
- Point
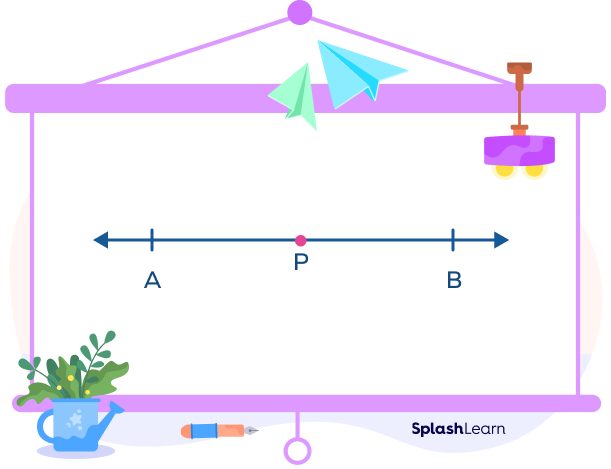
A point plays a crucial role in a segment bisector because it marks the midpoint of the line segment or point on the line that divides the line into two halves. Every line segment has a midpoint.
Here, the point ‘P’ is the midpoint of line segment AB. It bisects the line segment AB.
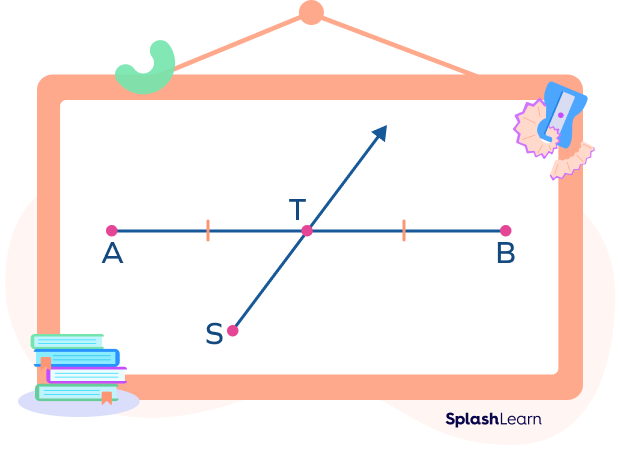
- Ray
A ray is a section or a part of a line that only has one fixed point and has no end at the other point. A ray as a segment bisector can be represented as shown in the figure below.
Here, ray ‘ST’ acts as a segment bisector of line segment AB.
- Line and line segment
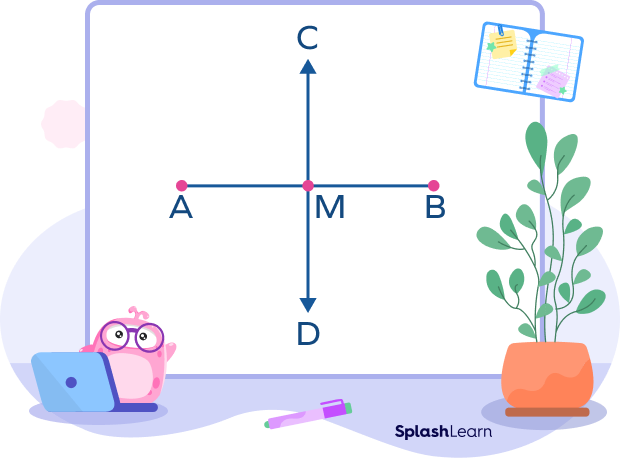
In geometry, a line is a straight one-dimensional figure that does not have a thickness, and it extends endlessly in both directions.
A line as a segment bisector can be represented as shown in the figure below. Also, any line segment on the line CD is also a segment bisector of AB.
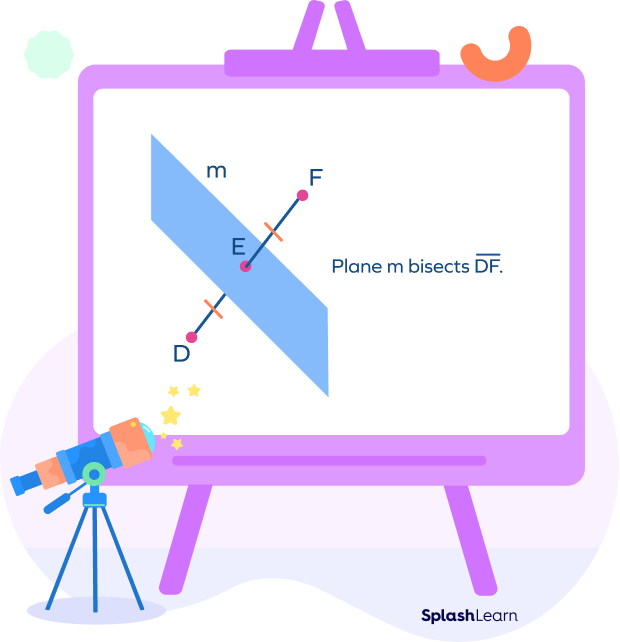
- Plane
A plane that passes through the midpoint of the line segment also acts as a segment bisector.
Segment Bisector and Midpoints
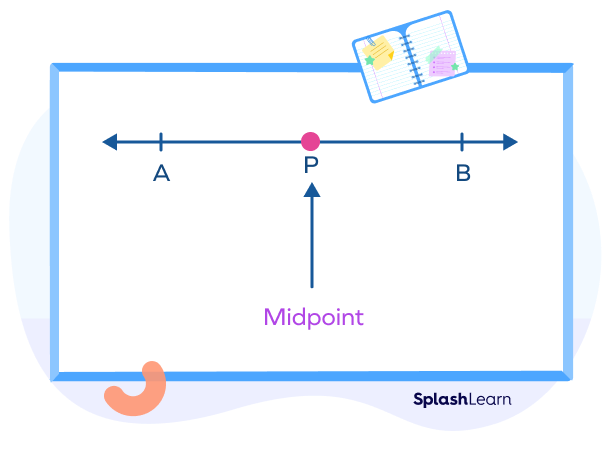
The midpoint of a segment bisector is the point at which the lines get divided into two equal halves. The midpoint for the two points is a point in the middle of the line that is equidistant from the two points.
Here, the point ‘P’ is the midpoint of line segment AB.
Segment Bisectors and Perpendicular Bisectors
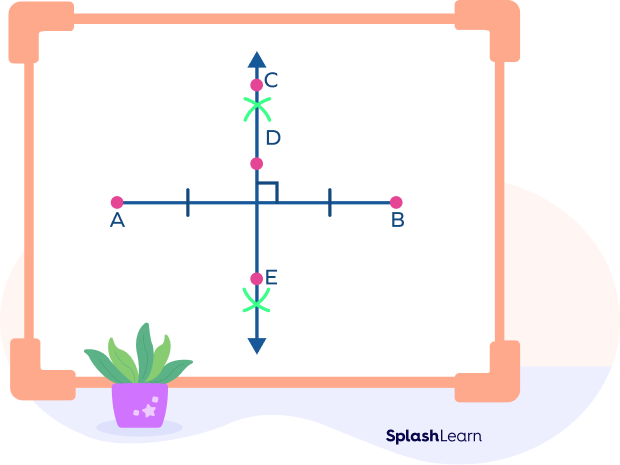
If a segment bisector is perpendicular to the line segment, it is known as a perpendicular bisector. In other words, a line segment that intersects another line segment at a right angle and divides it into two equal parts at its midpoint is known as a perpendicular bisector. Every line segment has only one perpendicular bisector.
In the given image, line CE is the perpendicular bisector of line segment AB.
How to Find the Segment Bisector of a Line
To find the segment bisector, identify the midpoint of that line segment and mark it with a point. A ray, or a line segment or a line passing through it is the required segment bisector.
- What is the segment bisector formula?
You can easily find the midpoint of a line segment using the midpoint formula if the coordinates of the endpoints are known. If the coordinates of the endpoints are given by (x1,y1) and (x2,y2), then the coordinates of the midpoint are given by
(xm, ym) = (x1 + x22,y1 + y22)
How to Draw a Bisector of a Segment
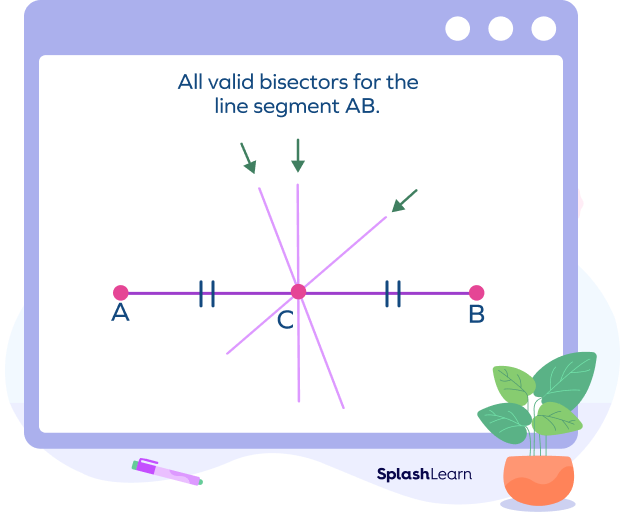
- Case 1: No constraints on the angle made by the bisector
When there are no restrictions on the bisector’s angle. The only thing left to do is figure out where the midpoint is. Mark The midpoint and draw the necessary bisector point, line, line segment, or ray through the midpoint.
As long a line or a segment or a ray passes through the midpoint, it is considered as a segment bisector. Note that infinitely many bisectors possible for a given line segment but only one perpendicular bisector.
- Case 2: Perpendicular Bisector
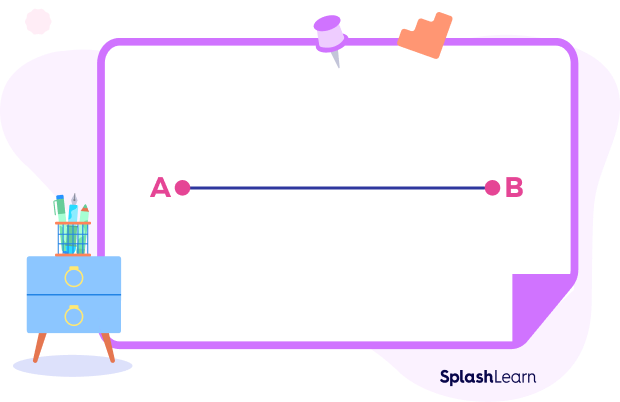
Using a compass and a ruler, follow these steps to draw a perpendicular bisector of a line segment.
Step 1: Draw a line segment AB.
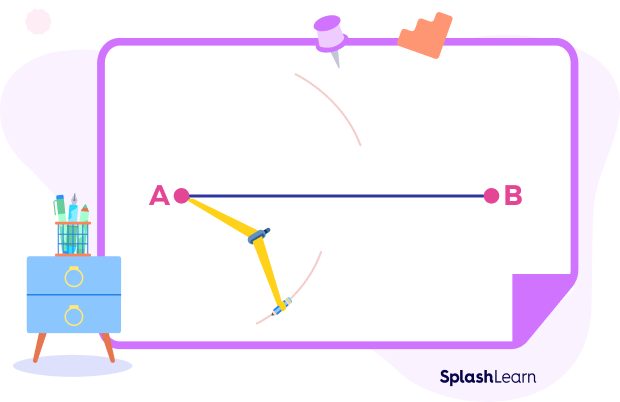
Step 2: Set the compass so that its length is slightly more than half of the length of AB. Place the compass pointer at point A and draw arcs below and above the line.
Step 3: Place the compass pointer at point B while maintaining the same length in the compass. Similarly, draw two arcs below and above the line.
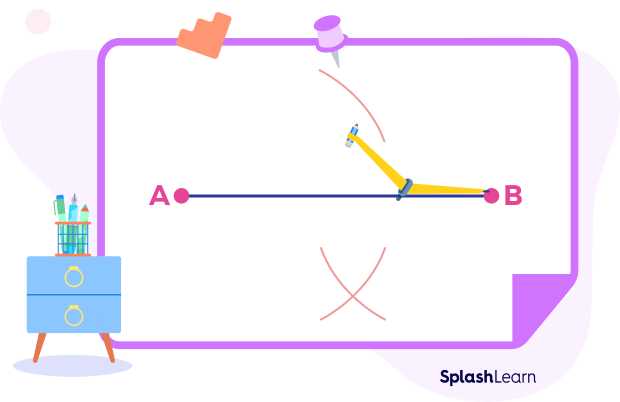
Step 4: Mark the points where the opposite arcs cut at points P and Q.
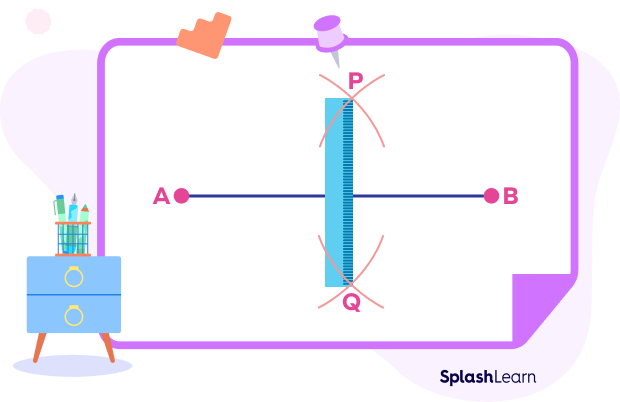
Step 5: Using a ruler, draw a line PQ, which is a required perpendicular bisector of a segment AB.
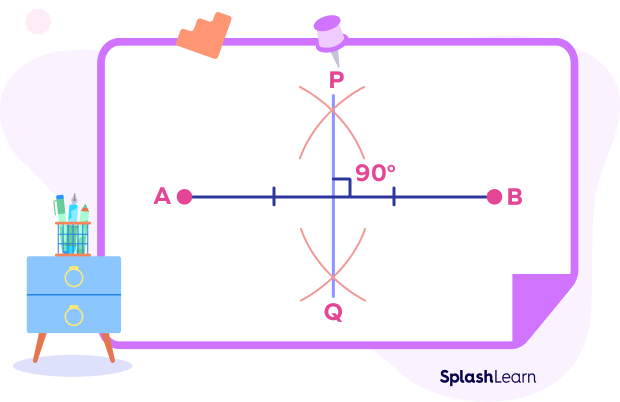
Facts about Segment Bisector
- A segment bisector always divides a segment into two equal parts by passing through its midpoint.
- A segment bisector may or may not be a perpendicular bisector.
- The perpendicular bisector of any line segment is unique.
Conclusion
In this article, we have learned the definition of a segment bisector, to identify the various forms of segment bisectors, such as line segments, lines, rays, and points and steps to find and draw segment bisectors.
Solved Examples on Segment Bisector
- If a bisector is drawn to a 14 inches long line segment, what is the measure of each part of the line segment?
Solution:
A bisector divides a line segment into two equal parts.
Given, the measure of the line segment is 14 inches.
The measure of each part thus formed = 142 = 7 inches.
- Identify whether the given figure is a ray, a line, or a segment of a line.
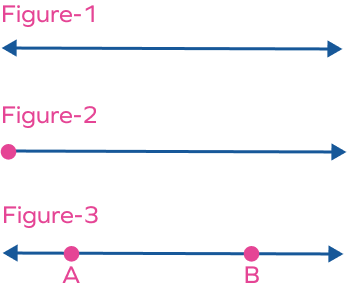
Solution:
Figure 1 is a line, Figure 2 is a line, and Figure 3 is a line segment,
- What information is enough to identify point D and ray CD as the segment bisector?
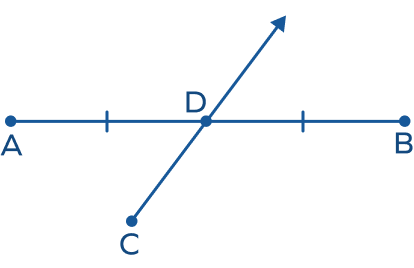
Solution:
If the point D is the midpoint of the segment AB, we can say that point D and the ray CD is the segment bisector.
- In the figure given below, find the value of ‘x’.
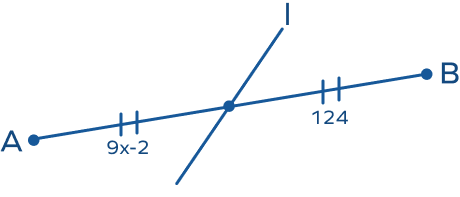
Solution:
In the given figure, line ‘l’ is a segment bisector.
So, 9x − 2 = 124
⇒ 9x = 124 + 2 = 126
⇒ 9x = 126
⇒ x $= \frac{126}{9} = 14$
Hence, the required value of ‘x’ is 14.
- Find the value of ‘x’ and ‘y’.
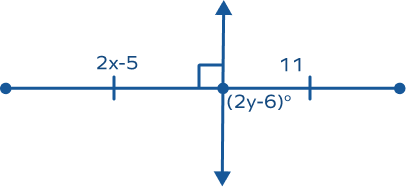
Solution:
In the given figure, the vertical line is a perpendicular bisector.
So, 2x − 5 = 11
⇒ 2x = 11 + 5
⇒ 2x = 16
⇒ x $= \frac{16}{2} = 8$
Also,
3y − 6 = 90
⇒ 3y = 90 + 6
⇒ 3y = 96
⇒ y $= \frac{96}{3} = 32$
Hence, the required value of ‘x’ and ‘y’ is 8 and 32 respectively.
Practice Problems on Segment Bisector
Segment Bisector - Definition, Types, Facts, Examples, FAQs
_____ has a line that has a fixed beginning and no definite end.
A segment of a line has a single endpoint and goes in the same direction forever known as a ray.
Point ‘B’ in the figure is _____.
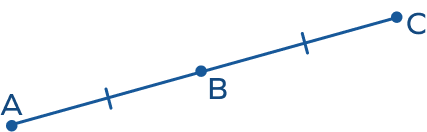
Point ‘B’ in the figure is the midpoint of line segment AC.
Which of the following is not a type of segment bisector?
Point, ray, and line are types of segment bisectors but the angle is not a segment bisector.
Frequently Asked Questions about Segment Bisectors
What are the different types of segment bisectors?
Different types of segment bisectors are point, ray, line, line segment, etc.
What is the perpendicular bisector?
A line segment that intersects another line segment at a right angle and divides it into two equal parts at its midpoint is known as a perpendicular bisector.
What is the point from which the segment bisector passes?
The point name of the point from which the segment bisector passes is the midpoint of the segment.
Which tool is used for drawing segment bisectors?
A compass and a ruler can be used to draw a segment bisector.
How many bisectors (lines) does a segment have?
We can draw infinitely many lines passing through the midpoint of the line segment that intersect the segment at different angles.


















