What Is a Superset?
We call set B a superset of set A if B contains all the elements of A. In other words, if A is a subset of B, then B is the superset of A.
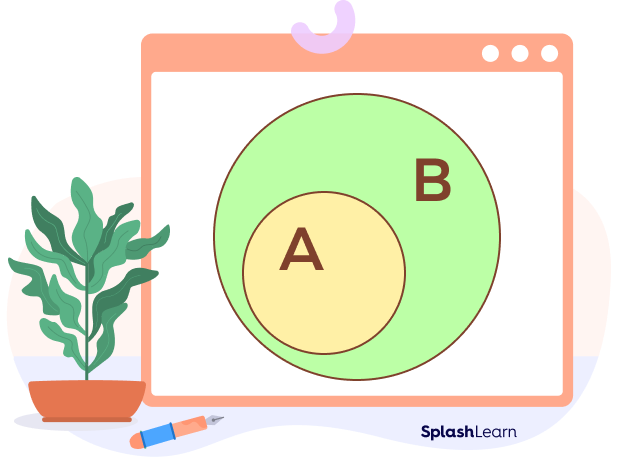
We know that set A is called a subset of set B if all the elements of A are present in B. Then what does superset mean? Let’s understand this with a Venn diagram.
In the following figure, set B contains set A.
A is a subset of B.
B is a superset of A.
Superset Meaning
In mathematics, a superset is a set that consists entirely of the elements of the smaller set. If P is the superset of Q, we can infer that Q is the smaller set and P contains all elements of Q.
Superset Definition
A superset of a given set is a set that contains all the elements of the given set.
If B is a superset of A, then A is a subset of B.
Example: A = {1, 2}, B= {1, 2, 3, 4, 5}
B contains all the elements of A.
Thus, B is a superset of A.
Also, A is a subset of B.
What Is a Proper Superset?
The proper superset or a strict superset is a superset that contains all the elements of the smaller set but also has some extra elements of its own.
If set B is the proper superset of set A, then all the elements of set A are in B, but set B must contain at least one element that is not present in set A.
Suppose we have two sets:
A={1, 3, 5}
B={1, 3, 4, 5}
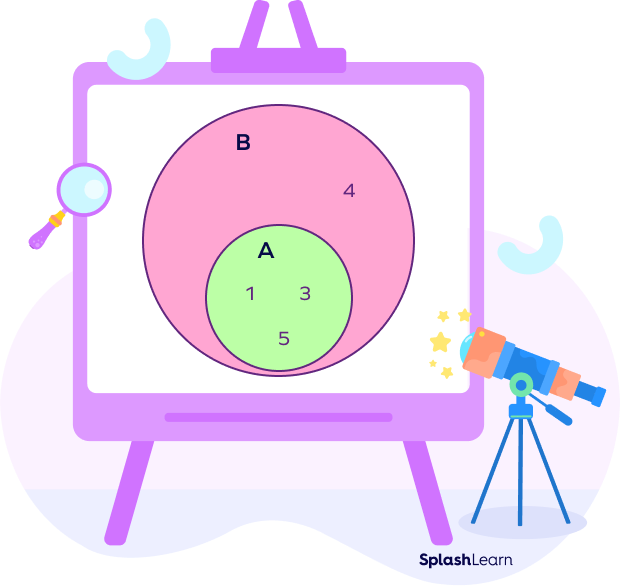
Here, B is a superset of A.
We can see that B is not exactly equal to A.
B contains the element 4, which is not present in A.
Such a superset is called a proper superset.
Superset Symbol
The symbols “⊃” or “⊇” are used to denote the superset.
- B ⊃ A means that B is a proper superset or a strict superset of set A such that A B (the sets are not equal.)
- B ⊇ A means that B is a superset of A, but the possibility of A = B is also considered.
Properties of Superset
- Empty set contains no elements. So, every set is a superset of the empty set.
For any set A, we have A ⊃ ∅.
- Every set is a superset of itself.
For any set A, we have A ⊇ A.
- For the given two sets (P and Q), if P ⊂ Q, then P ⊃ Q is true, indicating that subset and superset are opposite to one another.
- If B is a superset of A, then
A ∩ B = A
A ∪ B = B
- The cardinality of the superset is always greater than or equal to the other set.
Difference between Superset and Subset
| Subset | Superset |
|---|---|
| If A is a subset of B, the set A is contained in B. | If B is a superset of A, then B contains A. |
| A ⊂ B means that A is a proper subset of A. | B ⊃ A means that B is a proper or strict superset of A. |
| Subset is a smaller set compared to the other set. | Superset is a bigger set compared to the other set. |
| If A ⊂ B, then B ⊃ A. | If B ⊃ A, then A ⊂ B. |
| The empty set is a subset of every set. | Every set is a superset of the empty set. |
| Every set is a subset of itself. | Every set is a superset of itself. |
Facts on Superset
- A superset contains all the elements of the smaller set (it may or may not contain some extra elements as well.)
- The set of real numbers is a superset of the set of integers, the set of natural numbers, the set of rational numbers, the set of whole numbers.
- The set of whole numbers is a superset of the set of natural numbers.
N = {1, 2, 3, 4, …}
W = {0, 1, 2, 3, 4, …} - If A ⊂ B and B ⊃ A, then A = B
Conclusion
A superset is a set that contains almost all of the components of a smaller set that it is composed of. We understand that if B is contained within A, then A includes B. The following solved examples and practice problems will further ease understanding of the concept of supersets.
Solved Examples on Superset
1. Let Y= {1, 2, 3, 4, 5} and X= {1, 3, 5}. Identify the superset.
Solution:
Y= {1, 2, 3, 4, 5} and X={1, 3, 5}
Every element of X is also an element of Y.
The set Y contains the set X.
Y ⊃ X
Hence, Y is the proper superset of X.
2. E is the set of positive even integers. Write two supersets of E.
Solution:
E is the set of positive even integers.
E = {2, 4, 6, 8, 10, …}
We know that the set of integers is given by
Z = {…, -3, -2, -1,0, 1, 2, 3, 4, …}
Thus, Z is a superset of E.
The set of natural numbers is given by
N = {1, 2, 3, 4, 5, …}
Thus, N is a superset of E.
3. Let P is a set of all polygons. Identify the sets for which P will be a superset.
i) Set of convex polygons
ii) Set of quadrilaterals
iv) Set of triangles
v) Set of circles
vi) Set of 2D shapes
Solution:
P is a set of all polygons.
In geometry, a polygon can be defined as a flat or plane, two-dimensional closed shape bounded with straight sides. It does not have curved sides. Also, we need at least three sides to form a polygon.
i) Set of convex polygons will be a subset of the set P. Thus, P is a superset of the set of convex polygons.
ii) All quadrilaterals are polygons. So, the set P is a superset of the set of quadrilaterals.
iii) Triangles are the polygons with three sides. So, P is a superset of the set of triangles.
iv) Circles are not polygons since they are not formed by straight lines. Thus, P is not a superset of the set of circles.
v) Polygons are 2D shapes, but 2D shapes contain polygons and many other shapes like circles. So, the set of polygons is a subset of the set of 2D shapes. The set of 2D shapes is a superset of the set of polygons.
4. If A = {4, 5, 7, 8} and B = {4, 7, 8}, justify why A is a proper superset of B.
Solution:
A = {4, 5, 7, 8}
B = {4, 7, 8}
A is the proper superset of B because all elements of B are in A. The set A also has one extra element, 5, which is absent in B.
Practice Problems on Superset
Superset in Maths: Definition, Symbol, Properties, Example
If set C is a proper superset of B, then ______.
If C is a proper superset of B, then we represent it as $C \supset B$.
If X = {1, 2, 3}, Y= {}, Z = {1, 2}, then which of the following is true?
Every set is a superset of the empty set.
Also, here Z is a subset of X. Thus, X is a superset of Z.
Which of the following statements is not true?
The set of real numbers is the superset of the set of rational numbers.
Frequently Asked Questions about Superset
What is a proper subset?
If A is a proper subset of B, then all the elements of A are present in B, but A is not equal to B (B contains at least one extra element).
What are the symbols for a superset and a subset?
The superset is denoted by the sign “⊃” and the subset by the symbol “⊂.”
What is the universal set?
Universal set is a set that contains all the elements of all possible subsets under discussion.
Is every set a superset of an empty set?
Yes, since a null set has no elements, we can say that every set is thought of as the superset of a null set.
Can a set be a superset of itself?
Yes, a set is always thought of as a superset of itself since every set has all of its own elements.
















