What Is the Volume of a Hollow Cylinder?
The volume of the hollow cylinder can be defined as the space occupied by the hollow cylinder in a 3D plane. It is calculated by finding the difference between the volume of the outer cylinder and the inner cylinder.
A cylinder is made up of a rolled surface with a circular top and a circular base.
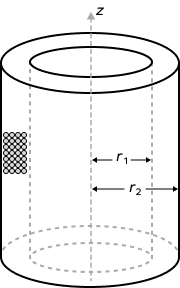
A hollow cylinder is also known as the cylindrical shell. It is empty from the inside and has some difference in its outer and inner radius. The space between the outer and inner cylinders defines the volume of the hollow cylinder.
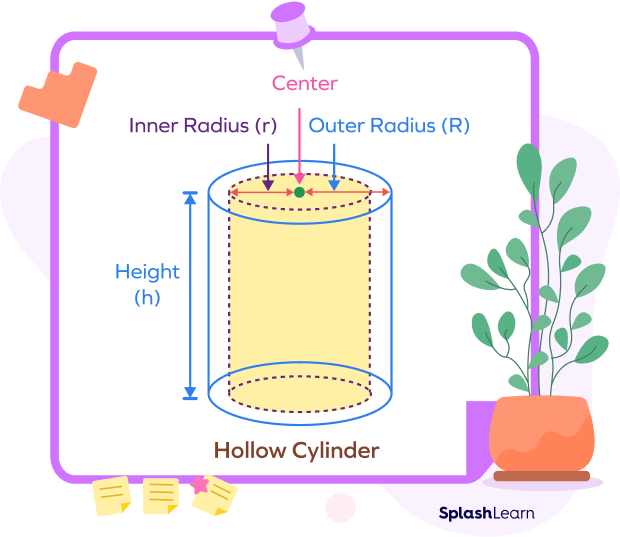
A hollow cylinder has some thickness at the peripheral. A cylinder is considered to be hollow from the inside if there is some difference between the internal radius and external radius
To put it another way, it is a cylinder that is hollow within and has some thickness at the edges.
Recommended Games
Volume of a Hollow Cylinder Formula
The formula for the volume of a cylinder can be used to determine the volume of a hollow cylinder. The volume of a hollow cylinder is equal to the difference in volume between the external and internal cylinders.
Note that the volume of a solid cylinder with radius r and height h is given by $= \pi r^{2}\;h$.
Volume of a hollow cylinder $=$ External cylinder volume $-$ Internal cylinder volume
- Volume of hollow cylinder using radius:
When the hollow cylinder’s outer and inner radii are known, its volume may be calculated as follows:
Volume of a hollow cylinder $= V =\pi (R^{2} \;–\; r^{2})$ h cubic units.
where
$R =$ outer radius
$r =$ inner radius
$h =$ height of the hollow cylinder
- Volume of hollow cylinder using diameter:
We know that diameter is twice the radius, $D = 2r$. So, if the diameter is given instead of the radius, we simply divide the value of diameter by 2 to get the value of radius, substitute the value into the above formula and solve the equation.
Recommended Worksheets
Volume of a Hollow Cylinder Derivation
To derive the volume of a hollow cylinder formula, we have to use the volume of the cylinder formula.
The formula to calculate the volume of a solid cylinder is given as,
Volume of a cylinder $=$ Base area$\times$ Height $= (\pi R^{2}) h$ cubic units
where,
$R =$ radius of a cylinder
$h =$ height of cylinder
The volume of a hollow cylinder having outer radius, “R” and inner radius, “r” can be written as the volume of a solid cylinder of radius, “R” and height, “h” minus the volume of a solid cylinder of radius, “r” and height, “h”,
Volume of a hollow cylinder $=$ Volume of External Cylinder $-$ Volume of Internal Cylinder
Volume of hollow cylinder $= \pi R^{2}\;h \;-\; \pi r^{2}\;h = \pi (R^{2}\;-\; r^{2})\;h$ cubic units
where,
$R =$ outer radius,
$r =$ inner radius, and,
$h =$ height of the hollow cylinder
How to Calculate the Volume of Hollow Cylinder
To calculate the volume of a hollow cylinder we have to follow the steps given below:
Step 1: Note down the given dimensions of the hollow cylinder. Make sure that they have the same units.
Step 2: Apply the formula and substitute the values to calculate the volume of a hollow cylinder.
Volume of hollow cylinder $= \pi (R^{2}\;-\;r^{2}) h$
Step 3: Solve the equation and represent the answer in cubic units.
Facts about the Volume of a Hollow Cylinder
- The volume of a hollow cylinder, also known as a cylindrical shell, is the difference between the volumes of two concentric cylinders.
- The volume of a hollow cylinder is affected by both the height and the difference in radii of the two cylinders.
- In a hollow cylinder, there are two circular bases in the shape of rings. The shape formed at the base is called an annulus ring.
- The bases of the cylinder are always congruent and parallel to each other.
- The height of the hollow cylinder is the perpendicular distance between its two circular bases.
Conclusion
In this article, we have learned about the hollow cylinder, its volume, formulas, and facts. Let us solve some volume of hollow cylinder examples and practice MCQs for better understanding!
Solved Examples on the Volume of a Hollow Cylinder
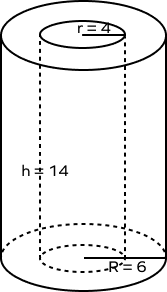
1. Find the volume of the given hollow cylinder.
Solution:
Here, $R = 6$
$r = 4$
$h = 14$
Volume of a hollow cylinder, $V = \pi (R^{2} \;–\; r^{2})\; h$ cubic units.
$= \frac{22}{7} \left[(6)^{2} \;-\; (4)^{2} \right]\times 14$
$= \frac{22}{7} ( 36 \;-\; 16 ) 14$
$= \frac{22}{7} (20) (14)$
$= 22 \times 20 \times 2$
$= 880$ cubic units.
The volume of the given hollow cylinder is 880 cubic units.
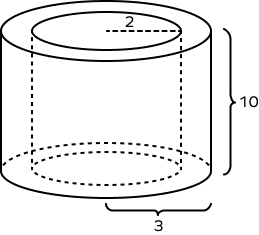
2. The figure shows a hollow cylinder with internal radius $= 2$ units, external radius $= 3$ units and the height $= 10$ units. Find the volume of the hollow cylinder.
Solution:
Volume of hollow cylinder $= \pi (R^{2}\;-\;r^{2})\;h$
$= \pi \times (9\;-\;4) 10$
$= 5 \times 3.14 \times 10$
$= 157$
Volume of metal used $= 157\; unit^{3}$.
3. Determine the inner radius of a hollow cylinder whose outer radius is 6 units, height is 10 units and volume is $847.8\; unit^{3}$. (Use $\pi = 3.14$)
Solution:
Outer radius, $R = 6$ units
Height $= 10$ units
Volume $= 847.8\; unit^{3}$
Substituting the values in the volume of the hollow cylinder formula,
$V = \pi (R^{2} \;–\; r^{2})\; h$
$847.8 = (3.14) \times (6^{2} \;-\; r^{2}) \times 10$
$\frac{847.8}{31.4} = 6^{2} \;-\; r^{2}$
$27 = 36 \;-\; r^{2}$
$r^{2} = 36 \;-\; 27$
$r^{2} = 9$
$r = \sqrt{9}$
$r = 3$ units
Therefore, the inner radius of a hollow cylinder is 3 units.
4. Calculate the height of a hollow cylinder whose outer radius is 9 units, the inner radius is 5 units, and the volume is $1408\; unit^{3}$. [Use $\pi = \frac{22}{7}$]
Solution:
We know that,
The volume of hollow cylinder, $V = \pi (R^{2} \;–\; r^{2})\; h$
$1408 = \frac{22}{7} (9^{2} \;-\; 5^{2})\times h$
$1408 = \frac{22}{7} (81 \;-\; 25 )\times h$
$1408 = \frac{22}{7} \times 56 \times h$
$1408 = 22 \times 8 \times h$
$1408 = 176 \times h$
$h = \frac{1408}{176}$
$h = 8$
The height of a hollow cylinder is 8 units.
Practice Problems on the Volume of a Hollow Cylinder
Volume of a Hollow Cylinder: Definition, Formula, Examples, FAQs
The volume of a solid cylinder is given by
The volume of a solid cylinder is given by $\pi r^{2}h$.
Volume of a hollow cylinder, $V =$ ________.
Volume of a hollow cylinder $=$ Volume of External Cylinder $-$ Volume of Internal Cylinder
Volume of hollow cylinder $= \pi R^{2}h\;-\;\pi r^{2}h = \pi(R^{2}\;-\;r^{2})\;h$ cubic units.
In the formula of volume of cylinder $V = (R^{2}\;-\;r^{2})\;h$, the term “R” stands for _______.
Volume of hollow cylinder $= \pi(R^{2}\;-\;r^{2})\;h$ cubic units
where,
$R =$ outer radius,
$r =$ inner radius, and,
$h =$ height of the hollow cylinder
Frequently Asked Questions on the Volume of a Hollow Cylinder
If the height of a hollow cylinder is doubled, how does the volume change?
We know that the volume of hollow cylinder $= (R^{2} \;–\; r^{2}) h$.
So, the height of a hollow cylinder has a direct relationship with the volume of the hollow cylinder. As a result, when the height of the hollow cylinder doubles, the volume also doubles.
What is a hollow cylinder’s annular ring?
An annular ring is a 2D object created at the bottom of a hollow cylinder. It is defined as a region surrounded by two concentric circles. The annular ring of the hollow cylinder is the base region of the cylinder.
What is the total surface area of a hollow cylinder?
Lateral surface area $= 2\pi Rh + 2\pi rh = 2\pi h (R + r)$
Area of 2 bases $= 2\pi R^{2} \;-\; 2\pi r^{2} = 2\pi (R^{2}\;-\;r^{2})$
Total surface area of hollow cylinder $=$ Lateral surface area $+$ area of solid basesTotal surface area of hollow cylinder $= 2\pi h(R + r) + 2\pi (R^{2}\;-\;r^{2})$
What is the annular ring of a hollow cylinder?
The 2D shape formed at the bottom of a hollow cylinder or the region bounded by two concentric circles is called the annulus or annular ring. The base area of the hollow cylinder is the area of the annular ring of the cylinder.


























