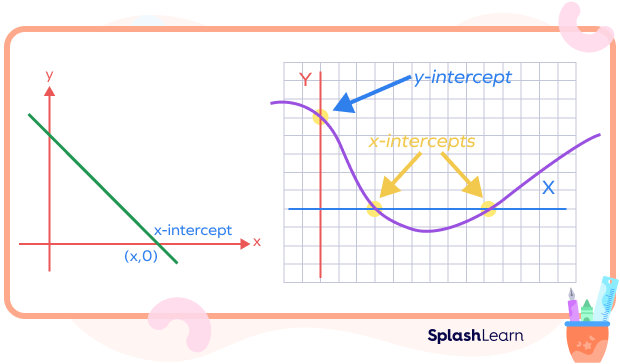
What Is X–intercept?
The x-intercept is a point where the graph of a function or a curve intersects with the x-axis of the coordinate system.
So, what does x-intercept mean on the Cartesian plane? The value of the x-coordinate of a point where the value of y-coordinate is equal to zero is known as the x–intercept. The x-intercept is also called “horizontal intercept.”
Recommended Games
X-Intercept Definition
For any line or a curve, the point at which the graph cuts the x-axis is called the x-intercept. For the x-coordinate, the value of the y-coordinate is zero.
Recommended Worksheets
X-Intercept on a Graph
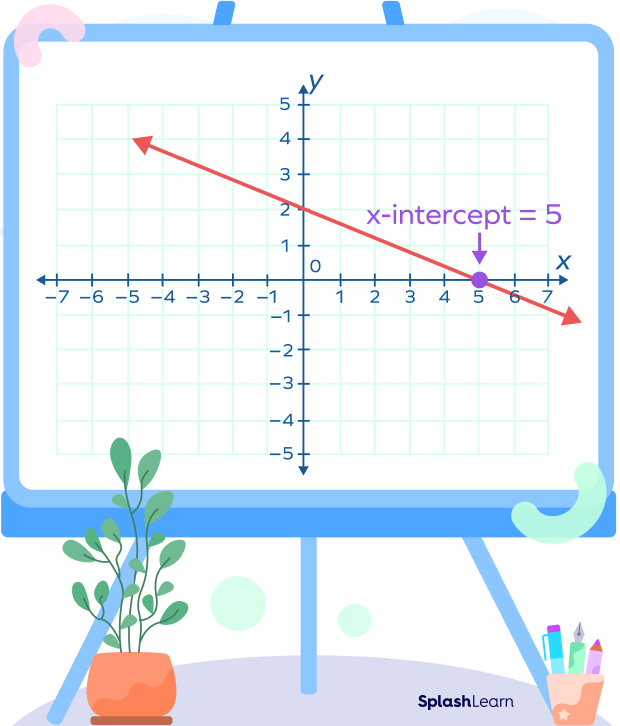
Let’s understand how to find x intercept on a graph. X-intercept is a point where the line crosses the x-axis.
Consider the line shown in the graph below. The line cuts the x-axis at point (5,0). Thus, the x-intercept of the line is 5.
X-Intercept Formula
We can find the x-intercept by substituting $y = 0$ in the equation of line. Let’s see how to get the x-intercept in terms of different forms of the equation of a line.
- The general form of a straight line is given by $ax + by + c = 0$, where a,b,c are constants.
If we substitute $y = 0$, we get
$ax + b.0 + c = 0$
$ax + c = 0$
$ax = \;-\; c$
$x = \frac{- c}{a}$
- The slope-intercept form of a straight line is given by $y = mx + c$, where m is the slope of the line and c is the y-intercept.
If we substitute $y = 0$, we get
$0 = mx + c$
$-\;c = mx$
$x = \;-cm$
- The point-slope form of a straight line is given by $y\;-\;b = m(x\;-\;a)$, where m is the slope of the line and (a,b) is a point on the line.
If we substitute $y = 0$, we get
$0\;-\;b = m(x\;-\;a)$
$\;-\;b = mx\;-\;am$
$am\;-\;b = mx$
$x = \frac{am\;-\;b}{m}$
- The intercept form of a straight line is given by $\frac{x}{a} + \frac{y}{b} = 1$, where a is its x-intercept and b is its y-intercept.
How to Find the X-Intercept
Let’s discuss three methods to find the x-intercept.
Finding X-intercept Using the Graph
Let’s understand how to find x-intercept on a graph. Consider the graph of a line given below:
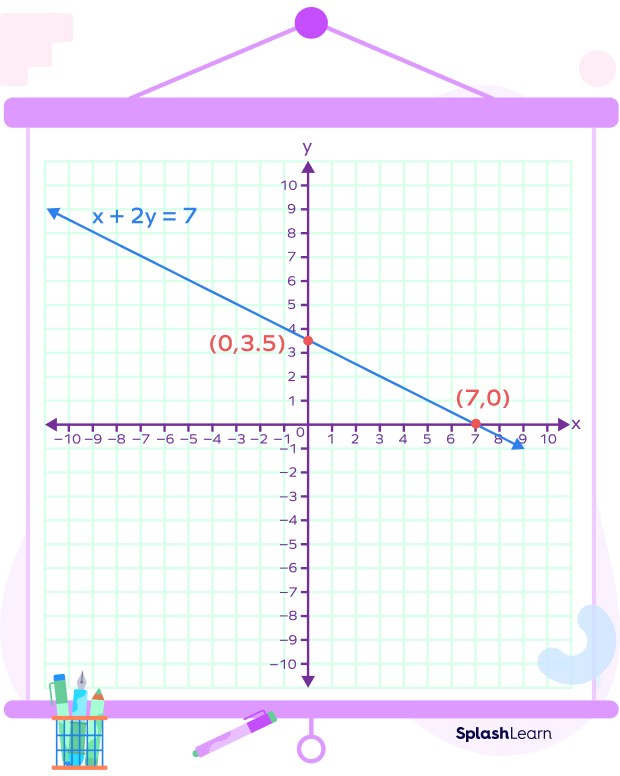
We can find the x-intercept from the graph by finding the point where the line touches the x-axis.
In this case, the line cuts the x-axis at 7.
So, x-intercept $= 7$
Finding X-intercept Using the Equation of a Line
The equation of a line is given by$ax + by + c = 0$.
Suppose we have a equation of a line $3x + 4y = 12$.
On converting it into general form, we get $3x + 4y\;-\;12 = 0$
x-intercept $= \frac{-c}{a} = \frac{-(-12)}{3} = 4$
Finding X-intercept Using the Quadratic Formula
The quadratic formula is given by: $ax^2 + bx + c = 0$
We can find the x-intercept using the formula: $x = \frac{-b \pm \sqrt{b^2 \;-\; 4ac}}{2a}$
Example: $x^2\;-\;5x + 6 = 0$
Here, $a = 1,b = \;-\;5, c = 6$
$x = \frac{5 \pm \sqrt{25 \;-\; 24}}{2} = \frac{5 \pm 1}{2}$
$x = \frac{4}{2},\;\frac{6}{2}$
$x = 2,\;3$
Finding Equation of a Line Using X-Intercept and Slope
Let’s understand how to find the equation of a line using x-intercept and slope with an example.
Example: Find the equation of a line with the slope = 3 and the x-intercept $= -4$.
We know that the general equation of a line with slope m is given by
$y = mx + b$
Using the formula of the x-intercept
$x = \frac{-b}{m}$
$-4 = \frac{-b}{3}$
$b = 12$
On substituting the value of c and m, we have
$y = 3x + 12$
Facts about X-intercept
A function may have one, 0, or many x-intercepts.The x-intercept is a point where the function crosses the x-axis. These points are also known as roots, zeros, and solutions.
Solved Examples on X-intercept
1. Find the x-intercept of the line $5x\;-\;6y + 15 = 0$.
Solution:
The equation of the line of the form $ax + by + c = 0$ has the x-intercept as $\frac{-c}{a}$.
In $5x\;-\;6y + 15 = 0,\; a = 5,\; b = -6,\; c = 15$
x – intercept $= \;-\;ca = -155 = \;-3$
Another way:
Simply substitute $y = 0$.
$5x\;-\;6(0) + 15 = 0$
$5x = -15$
$x = – 3$
2. What is the x-intercept of the quadratic equation given by: $2x^2 + 7x\;-\;9 = 0$?
Solution:
The quadratic formula of the form ax2+bx+c=0 has the x-intercept as $x = \frac{\;-b\pm \sqrt{b^2 – 4ac}}{2a}$.
Here, $a = 2,\;b = 7,\;c = -9$
So, x – intercept $= \frac{- \pm \sqrt{749\;-\;4\times 2\times (-9)}}{2\times2} = \frac{-7\pm \sqrt{49 + 72}}{2\times2} = \frac{-7\pm\sqrt{121}}{4} = \frac{-7\pm11}{4}$
$x = \frac{\;-\;7\;-\;11}{2},\;\frac{\;-\;7+11}{2}$
$x = \frac{-18}{2},\; \frac{4}{2} = \;-9,\;2$
3. Find the equation of the line if slope $= 6$ and the x-intercept $= 7$.
Solution:
We know that the general equation of a line with slope m is given by: $y = mx + c$. Using the formula of the x-intercept
$x = \frac{-c}{m}$
$7 = \frac{-c}{6}$
$c = -\;42$
On substituting the value of c and m, we have,
$y = 6x\;-\;42$
4. Find the x-intercept of a line passing through points (2,3) and (4,7)?
Solution:
The slope of the line passing through the points (2, 3) and (4, 7) is
$m = \frac{7 \;-\; 3}{4 \;-\; 2} = \frac{4}{2} = 2$
The equation of the line is: $y\;−\;b = m (x\;−\;a)$
$y\;−\;7 = 2(x\;−\;4)$
Substituting $y = 0$, we get
$\;-\;7 = 2(x\;-\;4)$
$\frac{-7}{2} + 4 = x$
$x = \frac{-7 + 8}{2} = \frac{1}{2}$
Practice Problems on X-intercept
X Intercept - Definition, Formula, Graph, Examples
We can find the x-intercept by
We can find the x-intercept by substituting $y = 0$ in the equation of the line.
The equation of line with slope $–\; 3$ and x-intercept 5 is
We know that the general equation of a line with slope m and y-intercept b is given by: $y = mx + b$.
Using the formula of the x-intercept
$5 = \frac{-b}{-3}$
$b = 15$
On substituting the value of c and m we have,
$y = 3x + 15$
In the graph given below, what is the x-intercept?
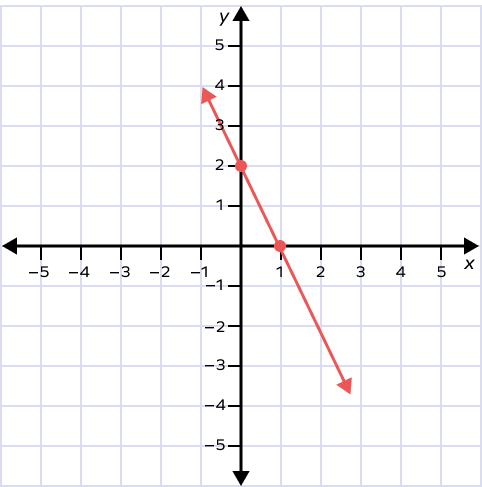
The line cuts the x axis at (1,0). So, the x intercept is 1.
What will be the x-intercept of $\frac{x}{3} + \frac{y}{7} = 1$?
In the intercept form of the equation of a line $\frac{x}{a} + \frac{y}{b} = 1$, the x-intercept is given by (a,0).
Here, $a = 3,\;b = 7$
So, x-intercept is 3.
Find the x-intercept for $y\;-\;3 = 2(x\;-\;4)$
Put $y = 0$
$-3 = 2(x\;-\;4)$
$-3 = 2x\;-\;8$
$2x = 5$
$x = \frac{5}{2}$
Frequently Asked Questions on X-intercept
Can x-intercept be 0?
Yes, the x-intercept is 0 for the line of the form $y = mx$, where m is the slope of the line.
What is the difference between x-intercept and y-intercept?
The x-intercept is the point where the graph cuts the x-axis, whereas y-intercept is the the point at which the graph cuts the y-axis.
How to find the y-intercept of a line using the equation?
To find the y-intercept, simply put $x = 0$ in the equation of the line and solve for x.




































