How To Convert 2 Radians to Degrees? Methods, Examples, FAQs

What Is 2 Radians to Degrees Conversion?

2 radians to degrees is approximately equal to 114.592°. 

2 radians to degrees in terms of $\pi = \frac{360^{\circ}}{\pi}$

Degrees and radians are the units used to measure angles. Let’s first understand what 1 degree and 1 radian represent to understand the 2 radians to degrees conversion.

Degree: A degree (denoted by °) is the amount of rotation from the initial arm to the terminal arm. A complete rotation or full turn around the center of a circle is 360°. If it is divided into 360 equal parts, each part represents 1 degree.

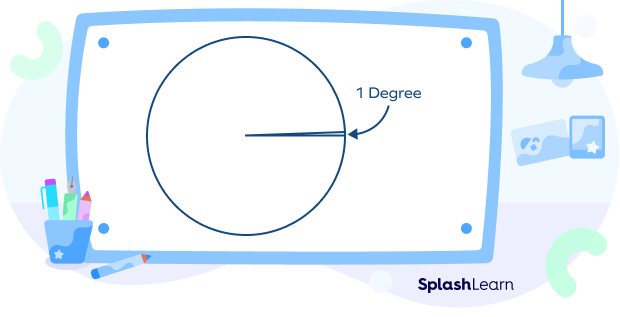
(Note: The figure shown above is not up to the scale.)

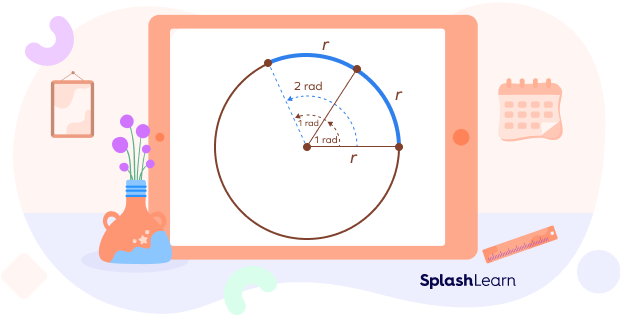
Radian: An angle of 1 radian is defined to be the angle, in the counterclockwise direction, which spans an arc whose length is equal to the radius of the circle. Thus, if arc length = r, then angle is 1 radian. This is true for all circles. 1 radian is quite big compared to 1 degree. 

1 rad ≈ 57.296° 

What Is Meant by 2 Radians to Degrees?

2 radians is the central angle made by an arc having arc-length equal to 2r which is basically the length of the diameter. Thus, when arc-length equals the diameter of the circle, the angle subtended by the arc is 2 radians. 

Note that if the arc-length equals the total circumference of the circle which is 2πr, it represents an angle of 2π radians. Thus, a complete circle represents 2π radians. 

1 rad ≈ 57.296°

2 rad ≈ 114.592°

How to Convert 2 Radians to Degrees

Let’s understand how to find 2 radians in degrees using different methods. 

• Using the approximate value of 1 radian in degrees
• Using the conversion formula 
• Using the relation $2\pi$ radians = 360°

Method 1

We know that 1 radian in degrees ≈ 57.296°

1 radian = 57.296°

On multiplying both sides by 2, we get

$2\times$ (1 radian) ≈ $2\times$ (57.296°)

2 radians in degrees ≈ 114.592°

Therefore, we get 2 radians to degrees approximately equal to 114.592°.

Method 2

In this method, we use the conversion formula for radian to degree for converting 2 radians to degrees.

For converting radian to degree, multiply the angle by $\frac{180^{\circ}}{\pi}$

Angle in degree = Angle in radian $\times \frac{180^{\circ}}{\pi}$

Here, angle in radian = 2 radians

Angle in degree = 2 $\times \frac{180^{\circ}}{\pi}$

Angle in degree ≈ 2 $\times$ 57.296°

Angle in degree ≈ 114.592°

Method 3

We know that the angle formed at the center of a circle is equal to 360°. 

360° in the form of radians is equal to 2 radians. 

$2\pi$ radians = 360°

Divide both sides of equation by .

2 radians = $\frac{360^{\circ}}{\pi}$

2 radians 114.592°

Therefore, we can use the 2 radians to degrees conversion to find the value of 2 radians to degrees.

Facts about 2 Radians to Degrees Conversion

Conclusion

In this article, we learned how to convert 2 radians to degrees using different methods. We also learned about degrees and radians in detail to understand the conversion. Let’s solve a few examples and practice MCQs.

Solved Examples on the 2 Radians to Degrees Conversion

Example 1: Convert 4 radians to degrees. 

Solution : 

2 radians to degrees is approximately equal to 114.592°. 

Thus, 4 radians = 2 $\times$ 114.592°

4 radians = 229.183°

Example 2: Convert 10 radians if 2 radians ≈ 114.592°.

Solution: 

2 radians ≈ 114.592°.

Multiply both sides by 5.

2 radians $\times$ 5 ≈ 114.592° $\times$ 5 

10 radians ≈ 572.958°

Example 3: Convert 0.2 radian to degrees. 

Solution: 

2 radians to degrees is approximately equal to 114.592°. 

2 radians ≈ 114.592°.

Divide by 10 on both sides.

Thus, 0.2 radian = $\frac{114.592^{\circ}}{10}$ = 11.459°

We can also do this another way.

We know that 1 radian ≈  57.296°

Therefore, 

0.2 radian ≈  0.2 $\times$ 57.296°

0.2 radian ≈  11.459°

Practice Problems on the 2 Radians to Degrees Conversion

Frequently Asked Questions about the 2 Radians to Degrees Conversion