What Is the (a + b)3 Formula?
In algebra, the (a + b)3 formula allows us to find the cube of a binomial and helps us to simplify expressions.
The formula for the cube of the sum of two terms, (a + b)3, can be expanded using the binomial theorem or by applying the distributive property multiple times. The result is:
(a + b)3 = a3 + 3a2b + 3 ab2 + b3
This formula shows how to find the cube of the sum of a and b by raising both terms to the power of 3, along with the combinations involving a and b raised to the power of 2 and 1.
Recommended Games
(a + b)3 Formula
The (a + b) whole cube formula or (a + b)3 formula represents the cube of a binomial. It represents the result of cubing the sum of ‘a’ and ‘b’.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
It’s important to note that this formula holds true for any values assigned to both ‘a’ and ‘b.’
Recommended Worksheets
Derivation of (a+b)3 Formula
To understand the derivation of the a + b whole cube formula, let’s start by expanding the expression (a + b)3.
We can achieve this by multiplying the binomial (a + b) by itself three times:
(a + b)3 = (a + b)(a + b)(a + b)
On expanding this expression, we get
(a + b)3 = (a2 + 2ab + b2)(a + b)
Let’s use the distributive property to expand the above expression.
(a + b)3 = a3 + a2b + 2a2b + 2ab2 + ab2 + b3
On combining like terms, we arrive at the final form of the (a + b)3 formula:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Alternatively, we can express the (a + b)3 formula as:
(a + b)3 = a3 + 3ab (a + b) + b3
This derivation showcases the algebraic manipulation required to arrive at the (a + b)3 formula.
How to Use the (a+b)3 Formula
Let’s use the formula (a + b)3 = a3 + 3a2b + 3ab2 + b3 to expand some expressions.
Example: (x + 2y)3
Here, a = x, b = 2x
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 2y)3 = x3 + 3x2 (2y) + 3x(2y)2 + (2y)3
(x + 2y)3 = x3 + 6x2y + 3x(4y2) + 8y3
(x + 2y)3 = x3 + 6x2y +12xy2 + 8y3
Facts about the (a+b)3 Formula
- The formula (a + b)3 represents the cube of the sum of two terms, “a” and “b.” (a + b)3 = a3 + 3a2b + 3ab2 + b3
- The a plus b whole cube formula represents the cube of the sum of “a” and “b.” It can also be expressed as (a + b)3 = (a + b)$\times$(a + b)$\times$(a + b).
- By the commutative property of addition, we have (a + b)3 = (b + a)3.
- The (a + b)3 formula is part of a group of related formulas known as the binomial coefficients, which are used to expand powers of binomials.
For example, (a + b)2 = a2 + 2ab + b2
- The coefficients of the terms in the expansion of (a + b)3 correspond to the numbers in the fourth row of Pascal’s Triangle. Pascal’s Triangle is a triangular arrangement of numbers where each number is the sum of the two numbers directly above it.
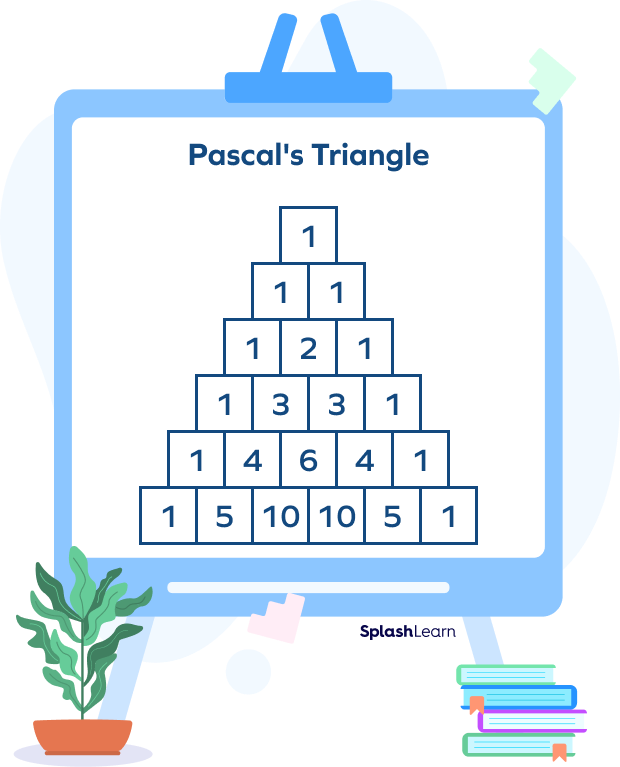
In the expansion (a + b)3 = a3 + 3a2b + 3ab2 + b3, the coefficients (1, 3, 3, 1) are the same as the fourth row of Pascal’s Triangle. This relationship between binomial expansions and Pascal’s Triangle extends to higher powers as well.
Conclusion
The (a+b)3 formula is a powerful tool in algebra for expanding and simplifying cubic binomials. By understanding its derivation, properties, and applications, you can enhance your problem-solving skills and tackle a wide range of mathematical challenges. Let’s solve some (a + b)3 formula examples and practice problems to understand the concept better.
Solved Examples on the (a+b)3 Formula
Example 1. Expand (x + 2)3.
Solution:
Using the (a + b)3 formula, we have:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 2)3 = x3 + 3x2(2) + 3x(2)2 + 23
Simplifying each term, we get
(x + 2)3 = x3 + 6x2 + 12x + 8
Example 2: Evaluate 143 using the (a + b)3 formula.
Solution:
Hare, we can write
143 = (10 + 4)3
Here, a = 10, b = 4
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(10 + 4)3 = 103 + 3(10)2(4) + 3(10)(4)2 + (4)3
(10 + 4)3 = 1000 + 3(100)(4) + 3(10)(16) + 64
(10 + 4)3 = 1000 + 1200 + 480 + 64
(10 + 4)3 = 2744
143 = 2744
Example 3: Find the coefficient of the term a²b in the expansion of (3a + 2b)³.
Solution:
Using the (a + b)3 formula, we get
(3a + 2b)3 = (3a)3 + 3(3a)2(2b) + 3(3a)(2b)2 + (2b)3
(3a + 2b)3 = 27a3 + 3(9a2)2b + 3(3a)(4b2) + 8b3
(3a + 2b)3 = 27a3 + 54a2b +36ab2 + 8b3
So, the coefficient of the term involving “a²b” is 54.
Practice Problems on the (a + b)3 Formula
$(A+B)^{3}$ Formula - Solved Examples, FAQS, Practice Problems
What is the expansion of $(a + b)^{3}$?
The correct expansion of $(a + b)^{3}$ is $a^{3} + 3a^{2}b + 3ab^{2} + b^{3}$.
What does $(a + b)^{3}$ represent?
The $(a + b)^{3}$ formula represents the cube of the sum of a and b
Which pattern do the coefficients in the expansion of $(a + b)^{3}$ follow?
The coefficients in the expansion of $(a + b)^{3}$ follow the arrangement of Pascal's triangle, where each coefficient is obtained by adding the two coefficients directly above it.
What is the expanded form of $(x + 2y)^{3}$?
The expansion of $(x + 2y)^{3}$ is obtained by applying the $(a + b)^{3}$ formula, resulting in $x^{3} + 6x^{2}y + 12xy^{2} + 8y^{3}$
Frequently Asked Questions about the (a + b)3 Formula
What is the purpose of the (a + b)3 formula?
The formula is used to expand and simplify cubic binomials, making algebraic manipulations easier.
Can the (a + b)3 formula be applied to other powers?
Yes, the formula is a specific case of the binomial theorem and can be extended to any positive integer power.
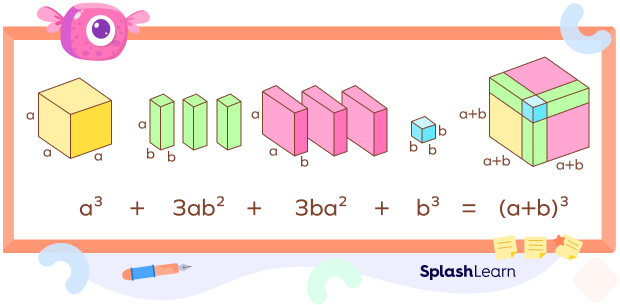
How can the (a + b)3 formula be proven geometrically?
By visualizing a cube with side lengths (a+b) and observing how its faces, edges, and corners correspond to the expanded terms.
What is the coefficient pattern in the expansion of (a + b)3?
The coefficients follow Pascal’s triangle: 1, 3, 3, 1.
How is the (a + b)3 formula related to real-world problems?
Can the (a + b)3 formula be used with negative values of “a” and “b”?
Yes, the (a + b)3 formula can be used with negative values of “a” and “b.” The formula works regardless of the signs of the variables.




































