What Is a Double?
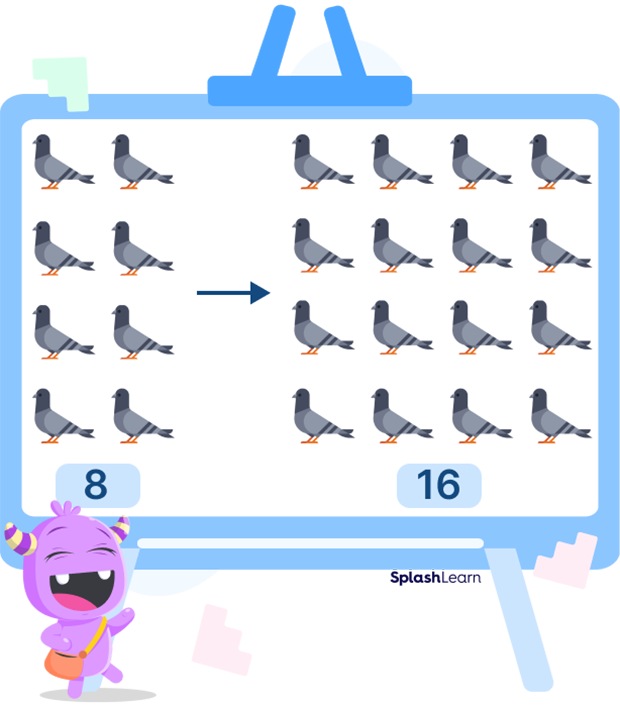
A magician has 8 pigeons. She covers them, waves her magic wand to show a “double trick!” What happens next? The pigeons double in number! So, how many pigeons does she have now? Let’s see!
Recommended Games
Double Meaning
Double numbers or doubles simply represent twice the given amount or number.
In the previous example, the pigeons double in number! It means that there are 16 pigeons now.
Recommended Worksheets
Double Definition
A double is a number or an amount that is twice as large as the given number or amount.
So, if we multiply a number by 2 or if we add a number to itself, we say that the number is doubled.
Let’s take a few more examples.
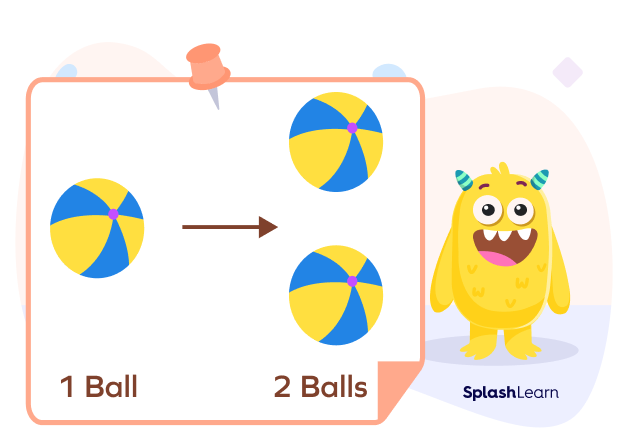
Doubling 1 ball results in 2 balls!
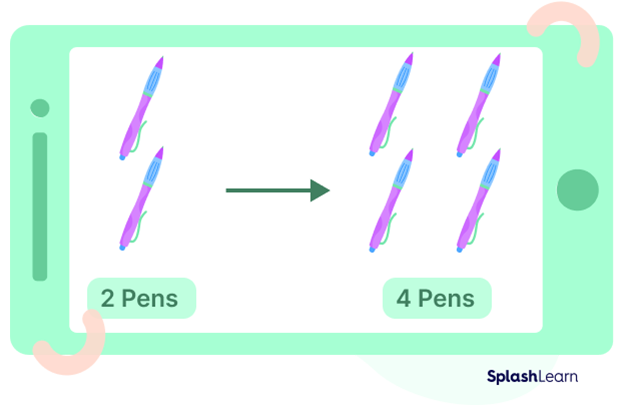
If we double 2 pens, we will get 4 pens!
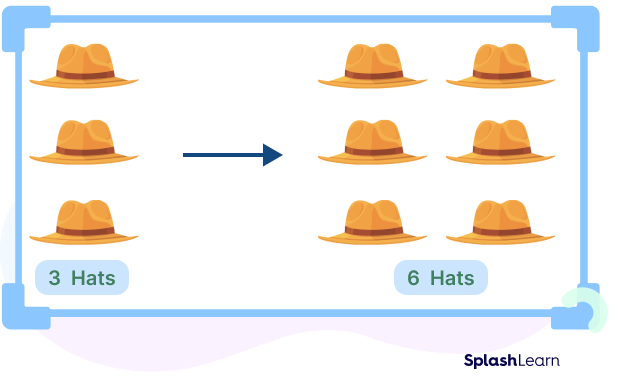
Double 3 hats and you get 6 hats!
Now, let’s double the numbers up to ten and make a chart. It is easy to remember the numbers we get by doubling one-digit numbers.

How to Double a Number?
Let’s discuss the formula for doubling numbers.
We can double any number in two ways.
1) Multiply the number by 2.
Double of $n = 2 \times n = 2n$
2) Add the number to itself.
Double of $n = n + n$
Example: Michelle has 4 balls, and Jane has double the number of balls that Michelle has. How many balls does Jane have?
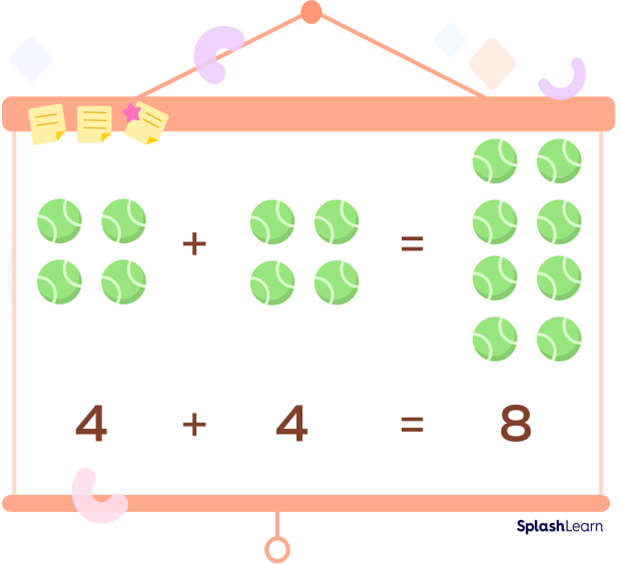
First, let’s double the number of balls Michelle has.
The double of four is $4 + 4 = 8$ or $4 \times 2 = 8$.
Therefore, Jane has eight balls.
Doubles in Action
In this section, we’ll see how we can use double of any number to solve some real-time math.
Doubles in Addition
Did you know that you can use doubles to add numbers?
The addition of two consecutive numbers can be done using the “double plus 1” or “double minus 1” or simply “near doubles” strategy.
Near Doubles
A near double is a number close to a double. For example, $7 + 8$ is considered a near double because it is close to the double number $7 + 7$. Near doubles could be doubles plus 1, doubles plus two, or doubles minus one.

Example: Evaluate $2 + 3$.
We can write 3 as $2 + 1$.
So, $2 + 3$ can be shown as:
$2 + 3 = 2 + 2 + 1$
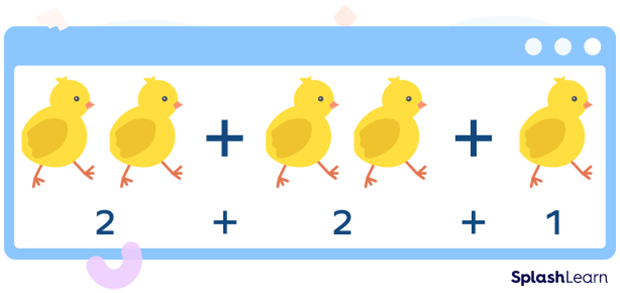
We know that the double of 2 is 4.
So, the required sum is one more than double, i.e., $4 + 1 = 5$.
Therefore, $2 + 3 = 5$.
Example: Evaluate $7 + 6$.
$6 = 7$ $–$ $1$.
So, $7 + 6$ can be shown as:

We know that the double of 7 is 14.
So, the required sum is one less than double, i.e., $14$ $-$ $1 = 13$.
Therefore, $7 + 6 = 13$.
“Double plus 1” and “double minus 1” are also called “near doubles” strategies.
You can also extend it to the numbers that are not immediately next to each other.
Doubles in Subtraction
We can subtract two numbers easily using doubles.
Example: Evaluate $12$ $-$ $6$.
We know that $6 + 6 = 12$. So, 12 is a double of 6.
$12$ $–$ $6 = 6$
We can illustrate it as:
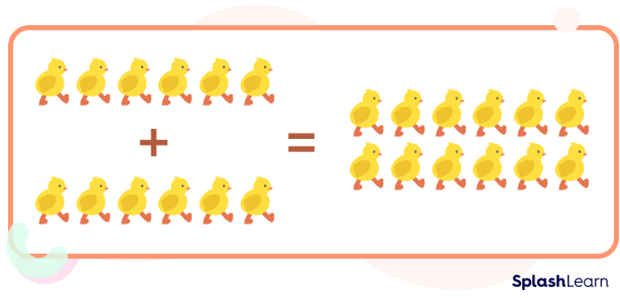
If we take away 6 from 12:
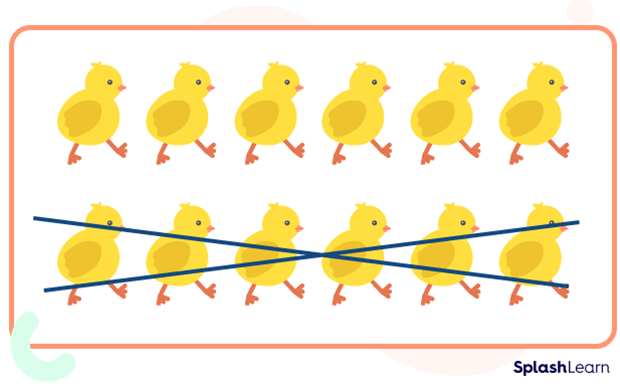
The remaining amount is 6.
Doubles Facts in Math
Let’s see some hacks that you can use to solve problems:
- If you subtract a number from its double, you will get the same number.
For instance, $12$ $–$ $6$ is 6.
- Since 2 + 3 is the same as $3 + 2$, we can apply any of the near doubles strategies to find the sum.
$2 + 3 = (2 + 2) + 1 = 4 + 1 = 5$
OR
$3 + 2 = (3 + 3)$ $–$ $1 = 6$ $–$ $1 = 5$ - If x is the factor of a number, its double will be a multiple of x.
For instance, 2 and 3 are factors of 6. The double of 6 is 12, a multiple of 2 and 3.
- The GCF of a number and its double is the number itself.
- The LCM of a number and its double is the double.
Solved Examples on Double
1. Joe has double the candies Jack has, Jack has double the candies Lily has, and Lily has double the candies Harry has. How many candies does Joe have if Harry has 2 candies?
Solution: Harry has 2 candies. So, Lily has 4.
Lily has 4 candies. So, Jack has 8.
Jack has 8 candies. So, Joe has 16.
Therefore, Joe has 16 candies.
2. What is the LCM (Least Common Multiple) of 9 and 18?
Solution: 18 is the double of 9. Since the LCM of a number and its double is the double number, the LCM of 9 and 18 is 18.
3. Evaluate $12 + 15$ using doubles.
Solution: We can write 15 as $12 + 3$.
So, $12 + 15 = 12 + 12 + 3$
$= (12 + 12) + 3$
$= 24 + 3$
$= 27$
Practice Problems on Double
Doubles in Math
Jane’s brother is double her age. If Jane is six years old, how old is her brother?
Jane is six years old. Her brother is double her age. So, her brother’s age is $6 + 6 = 12$ years.
What is the GCF (Greatest Common Factor) of 25 and 50?
The HCF of a number and its double is the number itself.
So, GCF of 25 and 50 is 25.
If 3 is a factor of a number x, then 2x will be a multiple of:
If 3 is a factor of x, 2x will be the multiple of 3.
Example: 3 is a factor of $\text{x} = 9$. Double of $\text{x} = 9$ is $2\text{x} = 18$ and it’s a multiple of 3.
Frequently Asked Questions on Double
Does the “doubles plus one” method apply to numbers more than 1000?
Yes, the doubles plus one method applies to all the counting numbers.
What is doubles minus one?
Doubles minus one is a strategy used to add two consecutive numbers. We simply add the bigger number twice or double it and then subtract 1 from it to get the final result.
What is the importance of the doubles strategy?
Children who can remember the double facts in math will be able to manipulate single-digit numbers more effectively and improve their ability to add and subtract.




































