What Is X Squared?
The term “$x$ squared” is an algebraic expression that represents x multiplied with itself.
Certain concepts can help simplify calculations in math. For example, multiplication simplifies addition when we have to add the same number multiple times.
Instead of writing $2 + 2 + 2 = 6$, we can write it as $2 \times 3 = 6$.
Similarly, a square of a number is a concept that simplifies multiplication. So, what does $x^2$ mean? It’s simple! The product of variable $x$ with itself is $x^2$.

Recommended Games
x Squared: Definition
For any variable x, x squared or $x^2$ is a mathematical notation that refers to a number being multiplied by itself. It represents the expression “$x \times x$” or “x times x”.
x squared symbol is $x^2$.
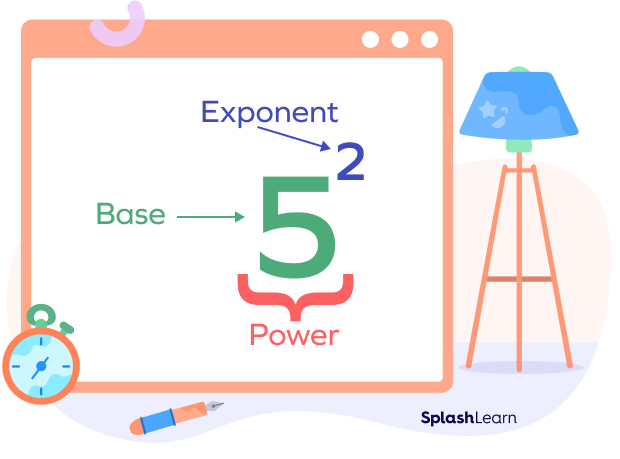
Here, $x$ is known as the base, and 2 is called the exponent. The whole expression $x^2$ is called the power.
If $x = 5$, then $x^2 = 5^2= 5 \times 5 = 25$
Here, 5 is the base, 2 is the exponent and the whole expression 52 is the power.
x2 can be written as different expressions in algebra. These expressions are:
- x × x
- x⋅x
- x(x)
- xx
Recommended Worksheets
How to Find the Value of x2 ?
x2 can be calculated by multiplying the value of x with itself.
Example 1: Let’s say x represents the number 7.
$x^2 = 7 \times 7 = 49$.
Example 2: x squared plus x squared equals 2 times x squared.
$x^2 + x^2 = 2x^2$
Example 3: x squared times x squared equals x to the power 4
$x^2 \times x^2 = x^4$
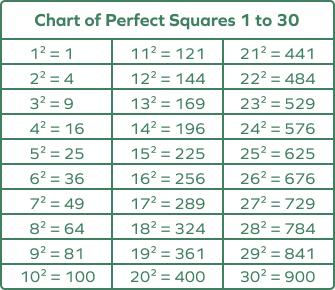
Perfect Squares
A perfect square is a number we get by multiplying an integer with itself. In other words, $x^2$ or x squared is called a perfect square if x is an integer.
Square Root of x
The square root of a number x is a number, which, when multiplied by itself, results in x.
Symbolically, it is written as follows:
Square root of $x = \sqrt{x} =$ $x^1/2$
The square of the square root of x is x itself.
For example, $(\sqrt{6} )^2 = 6$
The square root of x squared is either $+ x$ or $-x$, since
$x \times x = ($$-$$x) \times ($$-$$x) = x^2$
So, So, $\sqrt{x²} = \pm$ $x$
For example, $5^2 = 25$.
So, $\sqrt{25} = \pm$ $5$.
$5$ and $-$$5$ are both square roots of 25 since
$($ $-$ $5) \times ($$-$ $5) = 25$ and $5 \times 5 = 25$
Is x Squared the Same as 2x?
$x^2$ does not equal 2x.
$x^2$ involves a different operation than 2x.
x² is x multiplied by itself, which can be written as xx or x(x) as an algebraic term and is denoted by $x^2$.
In $x^2$, 2 is an exponent. It indicates that x is multiplied with itself two times.
$x^2 = x.x$
$2x$ represents x multiplied by the number 2.
In $2x$, $2$ represents the coefficient, which indicates that the number 2 is being multiplied by x, or two x’s are being added to each other.
$2x = x + x$
Example 1: If x equals 5, then
$x^2 = 5 \times 5 = 25$.
$2x = 2 \times 5 = 10$.
Example 2: If x equals 7, then
$x^2 = 7 \times 7 = 49$.
$2x = 2 \times 7 = 14$.
Algebraic Expression for (a + b)² and (a – b)²
In algebra, the square of the sum of two variables or $(a + b)^2$ can be expressed as $(a + b)(a + b)$. Solving this expression, we get:
$(a + b)(a + b) = a^2 + + ab + ab + b^2$
Therefore, $(a + b)^2 = a^2 + 2ab + b^2$
Similarly,
$(a$ $−$ $b)^2 = a^2$ $−$ $2ab + b^2$
Sum of Squares and Difference of Squares
The formula for the sum of two squares is:
$a^2 + b^2 = (a + b)^2$ $–$ $2ab$
The formula for the difference of two squares is:
$a^2$ $–$ $b^2 = (a + b)(a$ $–$ $b)$
Difference of Two Perfect Squares
When writing algebraic expressions as factors, the formula for the difference of two squares helps simplify complex algebraic expressions.
If we have to calculate the difference between the squares of two numbers X and Y, the algebraic expression will be $x^2$ $–$ $y^2$.
The formula to factorize this expression is as follows:
$x^2$ $–$ $y^2 = (x + y)(x$ $–$ $y)$
For example, let’s say $x = 5$ and $y = 3$.
$x^2$ $–$ $y^2 = 5^2$ $–$ $3^2$
$= (5 + 3) (5$ $–$ $3)$
$= 8 \times 2$
$= 16$
What Is Completing a Square?
Completing a square is a method used to change the form of a quadratic equation so that its LHS becomes a perfect square, which is also known as vertex form. We do this by rearranging the expression. The quadratic equation $ax^2 + bx + c$, after completing the square, has the form $a(x + d)^2 + e$.
Consider a quadratic equation $x^2+ 4x + 5$.
It is not a perfect square since it does not fit into the formula $(a + b)^2 = a^2 + 2ab + b^2$ .
We can rearrange the numbers and balance the equation to make it a perfect square.
Focusing on the first two terms, we set a $= x$ and b $= 2$
We know that, $(x + 2)^2 = x^2 + 2(2)x + 2^2 = x^2 + 4x + 4$
Let’s rewrite $x^2+ 4x + 5$ as
$x^2+ 4x + 5 = (x^2+ 4x + 4 ) + 1$
$= (x+2)^2+1$
Conclusion
X squared is a helpful notation that we use in math. It can be used in different kinds of algebraic expressions. It simplifies our calculations and allows us to develop formulas to solve problems quicker!
Solved Examples
1. Solve $x^2$ if $x = 8$.
Solution: Since $x^2 = (x)(x)$
$x^2 = 8 \times 8 = 64$
2. If $2x$ is $18$, what is $x^2$?
Solution: If $2x$ is $18$, then $x =\frac{18}{2}= 9$.
If $x$ is $9$, then $x^2$ is $9 \times 9 = 81$.
3. $12^2$ $-$ $5^2 =$ ?
Solution: We know that:
$x^2$ $-$ $y^2 = (x + y)(x$ $–$ $y)$
$12^2$ $-$ $5^2= (12 + 5) (12$ $–$ $5)$
$= 17 \times 7$
$= 119$
4. Solve the expression $(a+b)^2$ if $a = 5$.
Solution: $(a+b)^2 = a^2 + b^2 + 2ab$
$(5 + b)^2 = 5^2 + b^2 + 2(5b)$
$= 25 + b^2 + 10b$
5. Complete the square: $x^2+6x + 5$.
Solution: To complete the square, we write it as:
$x^2+6x+ 5 = (x^2+6x +9)$ $-$ $4$
$=(x+ 3)^2$ $-$ $4$
Practice Problems
X Squared
Which of the following is not an expression of $x^2$?
$2x$ is not an expression of $x^2$.
$2x$ means 2 multiplied by $x^2$.
$x^2$ means x multiplied by x.
If x is 6, calculate the difference between $x^2$ and $2x$.
$x^2 = 6 \times 6 = 36$
$2x = 2 \times 6 = 12$
So the difference will be:
$36 $-$ 12 = 24$.
If $x^2$ is $25$, what is $2x$?
If $x^2$ is $25$, then $x = \sqrt{25}$ $= 5$.
$2x = 2 \times 5 = 10$.
If x is 6, what is $\sqrt{x^2}$?
$x^2 = x$
So if x is 6, $\sqrt{x^2}$ will be 6.
$x^2$ $-$ $9 =$
$x^2$ $-$ $y^2 = (x + y)(x$ $-$ $y)$
$x2$$-$$9 = x2$$-$$32= (x + 3)(x$ $-$ $3)$
Frequently Asked Questions
Why do we call it “x squared”?
If a square has a side measuring x units, then the area of the square is x times x, which is $\text{x}^2$.
So, the product of a number with itself is called the “square” of a number.

What is the shape of the graph for $\text{x}^2$?
The graph of $\text{x}^2$ is the shape of a parabola.
x squared graph:

If $\text{x}$ is a negative number, will $\text{x}^2$ also be negative?
No, if $\text{x}$ is a negative number, then $\text{x}^2$ will be a positive number. This is because when you multiply a negative number by a negative number, you get a positive number as the product. Example: $($ $-$ $9)($ $-$ $9)=81$
Is 1 a perfect square?
Yes, a perfect square is an integer multiplied by itself. In other words, it is the square of $\text{x}$, where $\text{x}$ is an integer. 1 is a perfect square since $1\times1 = 1$
What is the importance of $\text{x}^2$ in math?
In math, $\text{x}^2$ is useful for simplifying algebraic expressions and arithmetic calculations. Instead of writing x times x along with other operations, we can simplify it to $\text{x}^2$.




































