Area of Sector of a Circle – Definition, Formula, Examples, FAQs

What Is the Area of a Sector?

The area of a sector is the area of the region enclosed by an arc and two radii of a circle. It represents a part of the area of a circle. Area of a sector is measured in square units, depending on the unit of the radius.

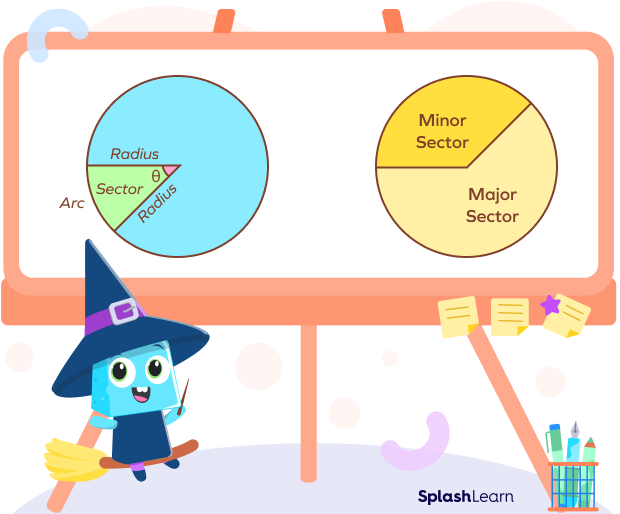
What Is the Sector of a Circle?

A sector is a part of a circle made of the arc of the circle along with its two radii. In the given diagram, the yellow region represents the sector of the circle. It is formed by two radii and an arc. The angle is the angle made by the sector at the center. 

Area of a Sector: Formulas

1) The formula to calculate the area of a sector of a circle when θ is in degrees is given by:

Area  of a sector $= \frac{θ}{360^{\circ}} \times \pi r^{2}$

where:

• θ is the angle of the sector in degrees (angle subtended by the arc at the center)
• r is the radius of the circle

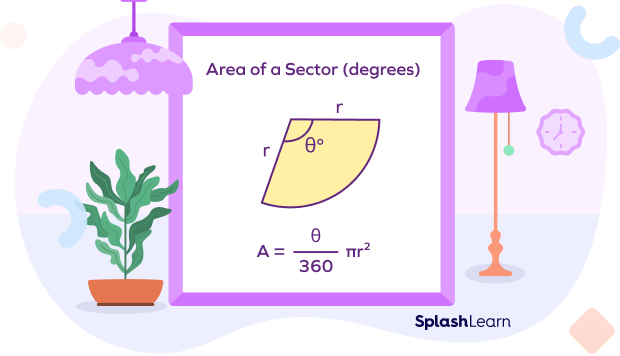
(Note: In the above diagram, the term ‘degrees’ simply signifies that this formula for the area of a sector is to be used when the central angle is given in degrees.)

2) The formula to calculate the area of a sector of a circle when θ is in radians is given by:

Area  of a sector $=(\frac{θ}{2}) \times r^{2}$

where:

• θ is the angle of the sector in radians
• r is the radius of the circle

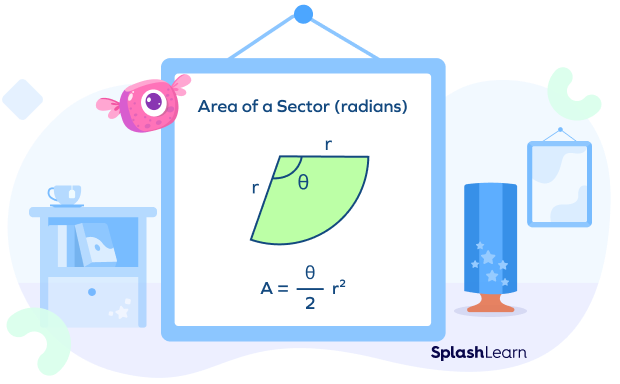
(Note: In the above diagram, the term ‘radians’ simply signifies that this formula for the area of a sector is to be used when the central angle is in radians.)

How to Calculate the Area of a Sector

Consider these steps to determine a sector’s area:

Step 1: Note down the radius and the central angle () of the sector.

Step 2: If the angle is in degrees, then substitute the values in the formula

Area $= (\frac{θ}{360^{\circ}}) \times \pi r^{2}$

Step 3: If the angle is in radians, then substitute the values in the formula

Area $= (\frac{θ}{2}) \times r^{2}$

Step 4: The area is measured in square units. Assign the appropriate unit.

Area of a Sector Formula: Derivation

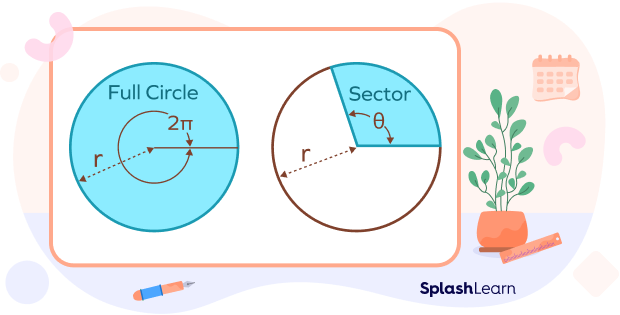
When angle is in degrees:

The angle made by a complete circle around the center is $θ = 360^{\circ}$.

Area of circle with radius $r  = \pi r^{2}$

There’s a direct relationship between the central angle and area.

Central angle ()	Area
$360^{\circ}$	$\pi r^{2}$
θ	$A = ?$

$\frac{Area\; of \;a\; sector}{Area \;of\; a \;circle} = \frac{Central \;Angle}{360^{\circ}}$

$\frac{A}{ \pi r^{2}} = 360^{\circ}$

$A = \frac{θ}{360^{\circ}} \times \pi r^{2}$

When angle is in radians:

The angle made by a complete circle around the center is $θ = 2\pi$.

Area of circle with radius $r  = \pi r^{2}$

Central angle ()	Area
$2\pi$	$\pi r^{2}$
θ	A = ?

$\frac{Area \;of \;a \;sector}{Area\; of \;a \;circle} = \frac{Central\; Angle}{2\pi}$

$\frac{A}{\pi r^{2}} = \frac{θ}{2\pi}$

$A = \frac{θ}{2\pi} \times \pi r^{2}$

$A = \frac{θ}{2} \times r^{2}$

Area of a Sector in Degrees

The area of a sector when the central angle (θ) is expressed in degrees, is given by

$Area = (\frac{θ}{360^{\circ}}) \times \pi r^{2}$

Example: Find the area of the given sector.

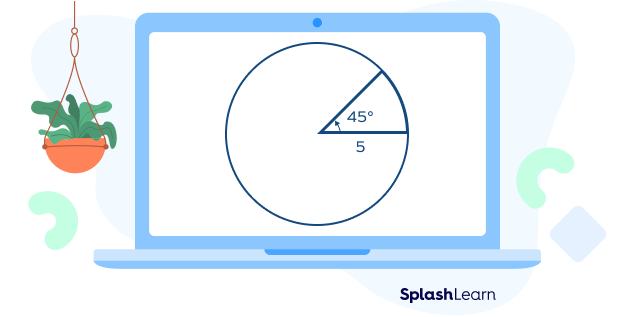
$r = 5$ units

$= 45^{\circ}$

Area $= (\frac{θ}{360^{\circ}}) \times \pi r^{2}$

Area $= (\frac{45^{\circ}}{360^{\circ}}) \times \pi (5)^{2}$

Area $= \frac{1}{8} \times 3.14 \times 25$

Area $= 9.8125$ square units

Area of a Sector in Radians

The area of a sector when the central angle (θ) is expressed in degrees, is given by

Area $= (\frac{θ}{2}) \times r^{2}$

Example: Find the area of the sector of the circle. (Use $\pi = 3.14$).

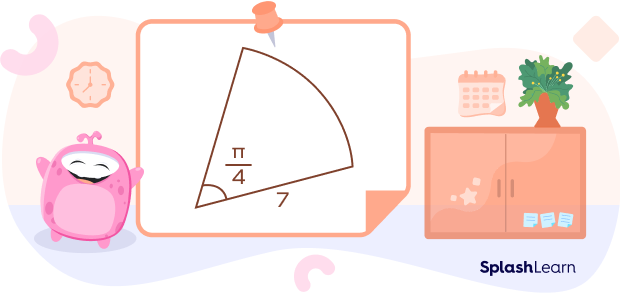
Area $= (\frac{\pi}{4 \times 2}) \times (7)^{2}$

Area $= (\frac{3.14}{4 \times 2}) \times (7)^{2}$

Area = 19.2325 square units

Facts about Area of a Sector

Conclusion

In this article, we learned about the area of a sector, its formulas, and also the derivation of the formulas. Let’s solve a few examples and MCQs for practice.

Solved Examples on Area of a Sector

Example 1: Find the area of the sector in terms of π if the circle has a radius of 8 units and a central angle of 45 degrees.

Solution: 

Using the formula for sector area, we write 

Area  $= \frac{θ}{360^{\circ}} \times \pi r^{2}$

Here, $r = 8$ units, $θ =45^{\circ}$

Area $= \frac{45^{\circ}}{360^{\circ}} \times π \times 8^{2}$

Area $= (\frac{1}{8}) \times π \times 64$

Area $= 8π$ square units

Example 2: A sector has a radius of 12 units and a central angle of 90 degrees. Calculate the area of the sector.

Solution: 

Area  $= \frac{θ}{360^{\circ}} \times \pi r^{2}$

Here, $r = 12$ units, $θ = 90^{\circ}$

Area $= \frac{90^{\circ}}{360^{\circ}} \times π \times 12^{2}$

Area $= \frac{1}{4} \times π \times 144$

Area $= 36π$

Area = 113.04 square units

Example 3: A sector has an area of 16π square units and a radius of 4 units. Find the central angle of the sector in radians.

Solution: 

 $r = 4$ units

Area of sector $= 16π$ square units

Area of sector $= (\frac{θ}{2}) \times r^{\circ}$

$16π = (\frac{θ}{2}) \times (4)^{2}$

$16π = (\frac{θ}{2}) \times 16$

\frac{θ}{2} = π$

$θ = 2π$

Central angle is 2π. It means that the given area is the area of the whole circle with radius 4 units.

Example 4: Find the area of a sector with a central angle of 60 degrees and a radius of 10 units.

Solution: 

Area $= (\frac{θ}{360^{\circ}}) \times \pi r^{2}$

Area $= (\frac{60^{\circ}}{360^{\circ}}) \times π \times 10^{2}$ 

Area $= (\frac{1}{6}) \times π \times 100$

Area $= 52.33$ square units

Practice Problems on Area of a Sector

Frequently Asked Questions on Area of a Sector