What Is the Base Area of a Cylinder?
The base area of a cylinder is the area of its circular base. If the radius of the circular base is r units, then the base area of cylinder is $\pi r^{2}$.
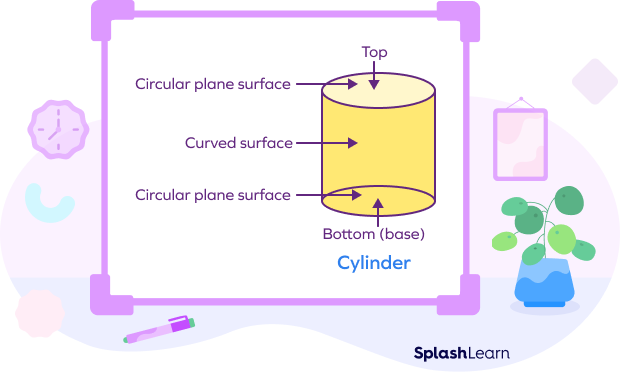
A cylinder is a geometric solid or a 3D shape with a curved surface and two circular bases.
Recommended Games
Base Area of Cylinder: Definition
The amount of space occupied by a flat circular surface lying at the bottom of the cylinder is known as the base area of the cylinder. The base of the cylinder is the circle. Hence, the base area of the cylinder is the area of the circle.
Recommended Worksheets
Base Area of Cylinder Formula
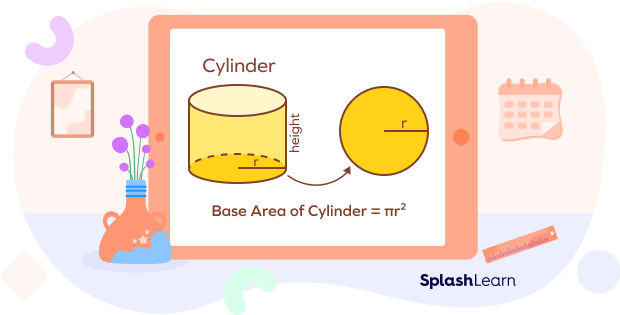
If “r” represents the radius of the circular base of the cylinder, then the base area of the cylinder is nothing but the area of a circle with radius “r.”
Area of a circle with radius $r = \pi r^{2}$.
Thus, the formula for the base area of cylinder is
Base Area of a Cylinder $= \pi r^{2}$
How to Find the Base Area of a Cylinder
Let’s understand how to find the area of the base of a cylinder.
Step 1: Note down the radius “r” of the given cylinder. If the diameter is given, divide it by 2 to find the radius.
Step 2: Substitute the value of “r” in the formula for finding the base area of the cylinder, given by
Base area of the cylinder $= \pi r^{2}$
Step 3: Assign the appropriate unit. Area is measured in square units.
Example: Find the area of the base of the cylinder with radius 7 feet.
Let radius $(r) = 7$ feet
Applying the formula, we get
Area $= \pi r^{2} = \frac{22}{7} \times 7 \times 7 = 154$ square feet
Using Base Area of Cylinder to Find Surface Area and Volume
The base area is commonly used to find the volume of solids like prisms, pyramids, etc. The volume of a 3D shape is generally calculated by multiplying the base area by its height. Let’s understand how to use the base area of the cylinder to calculate the total surface area and volume of the cylinder.
Surface Area of a Cylinder
The total surface area of a cylinder is the sum of the two circular bases and the curved surface area.
Base area of cylinder $= \pi r^{2}$
Thus, area of two circular bases $= 2\pi r^{2}$
Curved surface area $= 2\pi rh$
Total Surface Area $= 2 \pi rh + 2 \pi r^{2} = 2\pi r(r + h)$
Volume of a Cylinder
The volume of the cylinder is the total space occupied by the cylinder, which is the product of the base area and height.
$\text{Volume} = \text{Base area} \times \text{Height}$
Volume $= \pi r^{2} \times h$
Volume $= \pi r^{2}h$
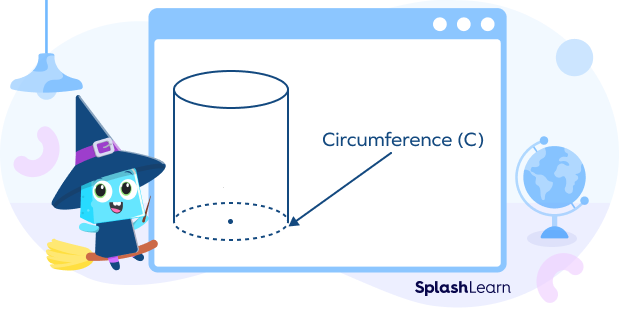
Circumference of the Base of a Cylinder
The circumference of the base of the cylinder can be defined as the circumference of the circle at the base of the cylinder. It is the length of the boundary of the circular base.
Formula for Circumference of Base of Cylinder
The formula for calculating the circumference of the base of the cylinder with radius r is the same as the circumference of the circle with radius r.
Circumference of the base of the circle $= 2\pi r$
(If the curved surface area of the cylinder is given, we can find the circumference of the base of the circle by dividing the curved surface area by the height of the cylinder.)
Facts about Base Area of a Cylinder
- The base area of an elliptical cylinder is the area of the ellipse at the base of the cylinder. It is given by ab, where a is the semi-major axis, and b is the semi-minor axis.
- The base area of the hollow cylinder is the area of the circular ring at its base. It is given by $(\pi R^{2} \;–\; \pi r^{2}) = \pi (R^{2} \;–\; r^{2})$, where R is the outer radius, and r is the inner radius.
Conclusion
In this article, we learned how to find the base area of a cylinder. We also learned how to use the base area of a cylinder to find the surface area and volume of a cylinder. Let’s solve a few examples and practice problems.
Solved Examples on Base Area of a Cylinder
1. If the radius of the cylinder is 0.07 inches, what will be the base area?
Solution:
Radius (r) $= 0.07$ inches
Base Area $= \pi r^{2}$
$= \frac{22}{7} \times 0.07 \times 0.07$
$= 0.0154$ square inches
2. Find the radius of the cylinder if the base area is 346.5 square units.
Solution:
Let radius be r units.
Base Area $= \pi r^{2}$
$346.5 = \frac{22}{7} \times r^{2}$
$r^{2} = \frac{346.5 \times 7}{22}$
$r^{2} = 110.25$
$r = 10.5$ inches
3. The circumference of the base of the cylinder is 88 feet. Find the base area of the cylinder.
Solution:
Circumference of the base of the cylinder $= 2r
$88 = 2 \times \frac{22}{7} \times r$
$r = \frac{88 \times 7}{2 \times 22}$
$r = 2 \times 7$
$r = 14$ feet
Base Area $= \pi r^{2} = \frac{22}{7} \times 14 \times 14 = 616$ square feet
4. The total surface area of the cylinder is 880 square inches. The curved surface area of the cylinder is 572 square inches. Find the base area.
Solution:
Total Surface Area of the cylinder $= 880$ square inches
Curved Surface Area of the cylinder $= 572$ square inches
Total Surface Area $=$ Curved Surface Area $+$ (2 Base Area)
$880 = 572 + $(2 Base Area)
2 Base Area $= 880 \;–\; 572$
2 Base Area $= 308$
Base Area $= \frac{308}{2} = 154$ square inches
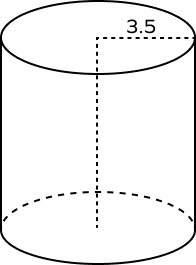
5. What is the base area of the given cylinder?
Solution:
Radius $= r = 3.5$ units
Base Area $= \pi r^{2}$
Base Area $= \pi r^{2} = \frac{22}{7} \times 3.5 \times 3.5$
Base Area $= 38.5$ square units
Practice Problems on Base Area of a Cylinder
Base Area of a Cylinder - Definition, Formula, Examples, FAQs
If the radius of the cylinder is 1 inch, what will be the base area?
Radius $(r) = 1$ inch
Base Area $= \pi r^{2} = \frac{22}{7} \times 1 \times 1 \approx 3.14$ square inches
Find the radius of the cylinder if the base area is 1386 square feet.
Let radius be r inches.
Base Area $= \pi r^{2}$
$1386 = \frac{22}{7} \times r^{2}$
$r^{2} = \frac{1386 \times 7}{22} = 441$
$r = 21$feet
The base area of a cylinder with radius “r” is given by
Base area of a cylinder with radius “r” $=\pi r^{2}$
Find the base area of the cylinder if the volume is 440 cubic inches and height is 22 inches.
Volume $= 440$ cubic inches
Height $= 22$ inches
Volume $=$ Base Area $\times$ Height
$440 =$ Base Area $\times 22$ Base Area $= \frac{440}{22} = 20$ square inches
A cylinder has a base area of 153.86 square inches. Find the radius of the cylinder $(\pi = 3.14)$.
Base Area $= 153.86$ square inches
$\pi r^{2} = 153.86$
$3.14 \times r^{2} = 153.86$
$r^{2} = 49$
$r = 7$ in
Frequently Asked Questions about the Base Area of a Cylinder
What is the base area of the cuboid?
The base of a cuboid is a rectangle. The formula for the base area of the cuboid is Length $\times$ Breadth.
What is the base area of a cube?
The base of a cube is a square. The formula for the base area of the cuboid is Side ✕ Side.
Is the base area of the cylinder the same as the cone?
If the circular base of the cone and the circular base of the cylinder have the same radius, then the base area of a cone equals the base area of a cylinder.
What happens to the base area of the cylinder if the radius is doubled?
The base area of the cylinder will become four times if the radius gets doubled.
Original radius $= r$
Original base area of cylinder $= \pi r^{2}$
New radius $= 2r$
New base area of cylinder $= \pi (2r^{2}) = 4\pi r^{2}$
What happens to the base area of the cylinder if the radius is halved?
The base area of the cylinder will become one-fourth times the original area if the radius is half the original radius.
How can we find the area of the base of a cylinder?
The area of the base of a cylinder is the area of the circle at the base of the cylinder. It is given by $\pi r^{2}$, where r is the radius of the cylinder.




































