Binary Division – Rules, Steps, Tricks, Facts, Examples, FAQs

What Is Binary Division?

The process of binary division is performed on binary numbers and it is pretty similar to the division of decimal numbers. The base of the binary number system is 2. It uses only two digits (0 and 1) when performing the division of binary numbers. The binary division procedure involves both binary multiplication and binary subtraction. 

The ‘bi’ in the term ‘binary’ means two. Several computer technologies are based on the binary number system. Therefore, it is crucial to understand the basic operations that you can carry out on binary numbers.

What Are Binary Division Rules?

To carry out our binary division, we must keep in mind the following four rules. 

Binary Division Rules:

• Dividing 1 by 1 gives 1.
  
  1 ÷ 1 = 1

• Dividing 0 by 1 gives zero.
  
  0 ÷ 1 = 0

• Dividing 0 by 0 is meaningless.
  
  0 ÷ 0= Meaningless

• Dividing 1 by 0 is meaningless. 
  
  1 ÷ 0 = Meaningless

Let’s summarize!

Binary Division Rules
1 ÷ 1 = 1
0 ÷ 1 = 0
Division by 0 is meaningless. 1 ÷ 0 = Meaningless 0 ÷ 0 = Meaningless

These four rules must be followed when carrying out binary division.

How To Do Binary Division

There are different ways to do binary division. The simplest way is the long division method. Just like decimal division, there are four key steps involved in the binary division.

• Divide the suitable digits of the dividend and record the quotient.
• Multiply the divisor by the quotient and write the product below.
• Subtract the product from the dividend and write the difference below.
• Bring down the next digit and repeat.

Let’s recall the binary subtraction and binary multiplication rules as we will be using those in the long division method.

Binary Subtraction Rules:

• 0 – 0 = 0
• 1 – 0 = 1
• 1 – 1 = 0
• 0 – 1 = 1 (Borrow 1)

Binary Multiplication Rules:

• 0 × 0 = 0
• 0 × 1 = 0
• 1 × 0 = 0
• 1 × 1 = 1  [borrow or carry over is not applicable.]

Binary Long Division

The process of binary long division is similar to that of the decimal number system. It comprises dividing, multiplying, subtracting, and bringing down.

Let’s understand the binary division with steps. 

Step 1: Compare the first two numbers of the dividend with the divisor. If the divisor is larger, write 0 as the quotient, then bring the second bit of the dividend down. If the divisor is smaller, multiply it with 1 and the result becomes the subtrahend. Add the suitable number in the quotient place. 

Step 2:  Multiply the divisor by the number written at the quotient and subtract the value.

Step 3: Now, bring down the next number (bit) of the dividend and repeat the first two steps. 

Step 4: Repeat the process till you get remainder 0 or reach the end of the dividend. 

The resultant quotient will be your answer.

Example 1: 1110 ÷ 111

Dividend = 1110

Divisor = 111

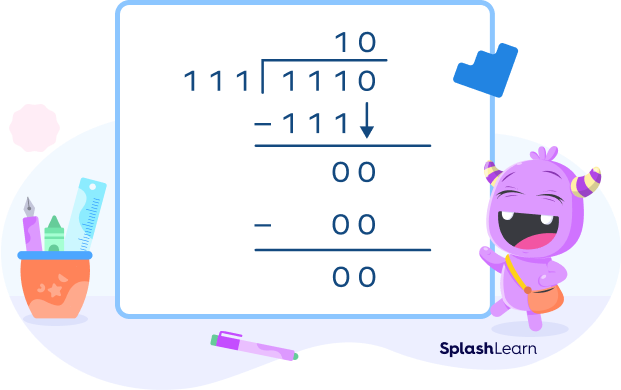
Let’s understand the steps we followed here.

Step 1:  Comparison.

Comparing the divisor 111 and the first digit of 1110, we get

• 111 > 1 (divisor is larger) 

So we can write 0 at the first place of the quotient and move ahead to compare the first two digits.

• Next, 111 > 11 (divisor is larger)

Again write 0 at the quotient place (now there are two 0’s) and move ahead.

• Next, 111 = 111 

Thus, write 1 as the third digit of the quotient.

Step 2: Multiply and subtract.

111 multiplied by 1 is 111. 

Write 111 below 111 and subtract.

Subtracting 111 from 111 results in 0.

Step 3: Bring down.

Bring down the next digit of the dividend which is 0.

Now we will repeat the first two steps.

111 > 00 (divisor is larger than the dividend).

So, we place 0 at the quotient and get the remainder 0.

The answer here is 0010₂.

We can ignore the first two insignificant digits.

Thus, 1110₂ ÷ 111₂ = 10₂

Example 2: 11100 ÷ 10

Dividend: 11100

Divisor: 10

Now, the division can be carried out in a step-by-step process, as you would do for a decimal number. 

The quotient is 1110₂.

11100₂ ÷ 10₂ = 1110₂

How to Verify Your Answer in the Binary Division (Bold)

Here is how you can verify the answer of the binary division problem using the decimal number system. In the previous example, we calculated

11100₂ ÷ 10₂ = 111010₂

Here,

(11100)₂ = 28

(010)₂ = (10)₂ = 2

We know that 28 ÷ 2 = 14.

So, the binary equivalent of 14 is 1110₂.

Thus, the answer is correct. 

Facts about Binary Division

You can also perform binary division by first converting the two binary numbers (dividend and divisor) to decimal numbers. Divide them by the regular decimal long division and convert the resulting quotient back to binary form.Just like in the binary division, division by 0 is also not defined in the decimal system.

Conclusion

The binary division can be performed easily using the long division method. In this article, we learned about the binary division, its rules, formulas, steps for the long division method and a variety of examples. Let’s solve a few examples based on the binary division and try to solve a few MCQs.

Solved Examples on Binary Division

Example 1: Divide: 10010 by 11.

Solution: 

Divisor: 11 

Dividend: 10010

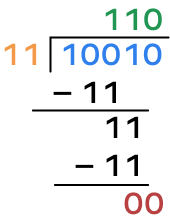
Here’s how we do it:

Step 1: Compare dividend and divisor.

• 11 > 10 (divisor is larger)

So, write 0 at the first position of the quotient and move ahead.

• 11 < 100 (divisor is smaller)

Write 1 at the next position in the quotient. 

Step 2: Multiply and subtract.

11 multiplying by 1 is 11.

Subtracting 11 from 100, we get 1.

Here’s how we do the binary subtraction. (Check out the binary subtraction rules mentioned earlier to understand this.) 

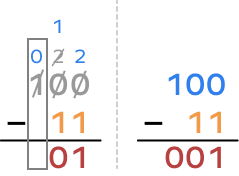
Step 3: Bring down.

Bring down the next digit of the dividend, which is 1.

Now, we need to divide 11 by 11.

It is simple. Write 1 at the next position in the quotient.

11 multiplied by 1 is 11.

11 subtracted from 11 is 0.

Thus, 10010₂ ÷ 11₂ = 110₂

Example 2: Divide 100100₂ by 100₂.

Solution: 

Dividend: 100100₂

Divisor: 100₂

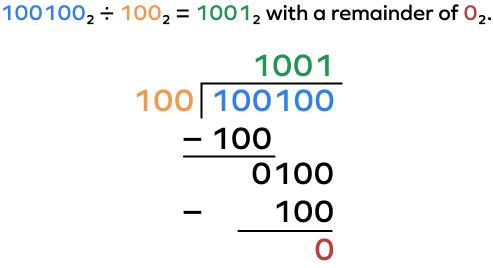
Thus, 100100₂ ÷ 100₂ = 1001₂ 

Example 3: Find the answer of the binary division 10101₂ ÷ 11₂ 

Solution:

10101₂ ÷ 11₂ = 111₂

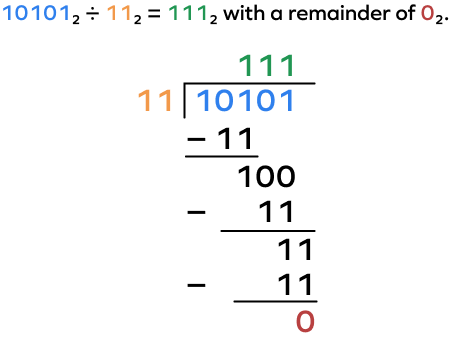
Practice Problems on Binary Division

Frequently Asked Questions about Binary Division