What Does Circumscribed Mean in Math?
A circumscribed shape means a shape drawn around another shape such that it is touching it at points (vertices) but not cutting it.
When a shape is restricted within another shape and there is no way for the inside figure to pass through the outer figure, then we say that the inner shape is circumscribed by the outer shape. The outer shape touches the maximum number of points of the shape inside without crossing it.
To circumscribe means to restrict someone’s or something’s freedom. The prefix “circum” means “around,” and “inscribe” means “to be within the boundaries of.” Thus, “circumscribed” means a shape is drawn around another shape.
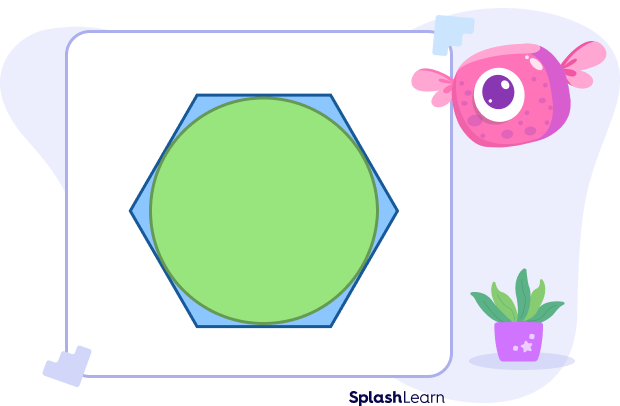
Example 1: Circumscribed hexagon
Here, a hexagon is drawn around a circle touching the maximum number of points on the circumference but not crossing it.
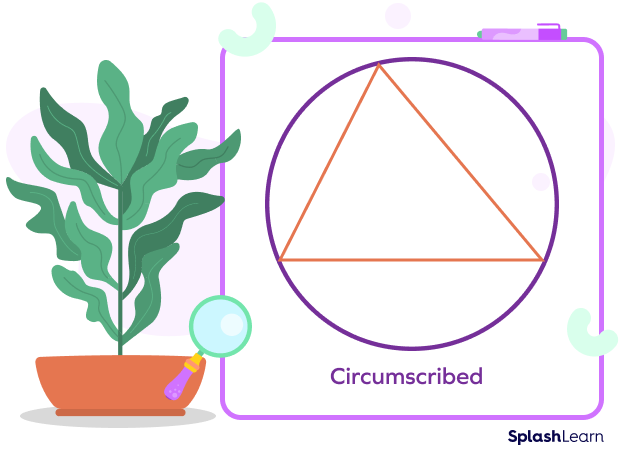
Example 2: Circumscribed circle or circumcircle
Here, a circle is drawn around a triangle such that the circle passes through all the three vertices of the triangle. This is termed the circumcircle of a triangle.
Circumscribe: Definition
Circumscribe means to draw a shape around another shape such that the outer shape touches maximum points of the inside shape but not crossing it such that the inside shape is enclosed or restricted within the bounds of the outer shape.
Circumscribed Circle
The circle that passes through all the vertices of another geometrical figure or a polygon but does not cross it is called “circumscribed circle” or “circumcircle.”
When a circle circumscribes a quadrilateral, the quadrilateral is called a “cyclic quadrilateral.” The sum of the opposite angles of a cyclic quadrilateral equals 180 degrees.
Take a look at a square circumscribed by a circle. Here, the diameter of the square equals the diagonal of the square.

Diagonal of a square $= \sqrt{2}$ × (side of the square) = $\sqrt{2}$ × s
Thus, the diameter of the circle $= \sqrt{2}$ × (side of a square)
Using this formula, you can determine the side of the square if the diameter of the circle is given.
Circumcircle radius = Radius of the circle $= \frac{\sqrt{2} \times (side \;of \;a \;square)}{\sqrt{2}} = \frac{side\; of\; the\; square}{\sqrt{2}}$
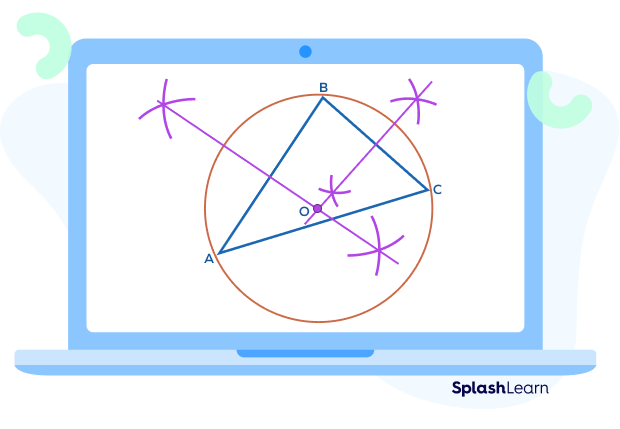
Steps to Construct a Circumcircle of a Triangle
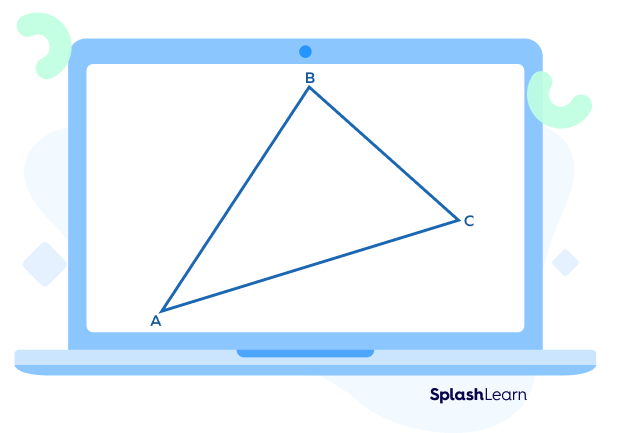
Let’s understand the steps for constructing a circumcircle of a triangle.
Step 1: Construct a triangle with the required angle measurements.
Step 2: Draw perpendicular bisectors of two sides of the triangle.
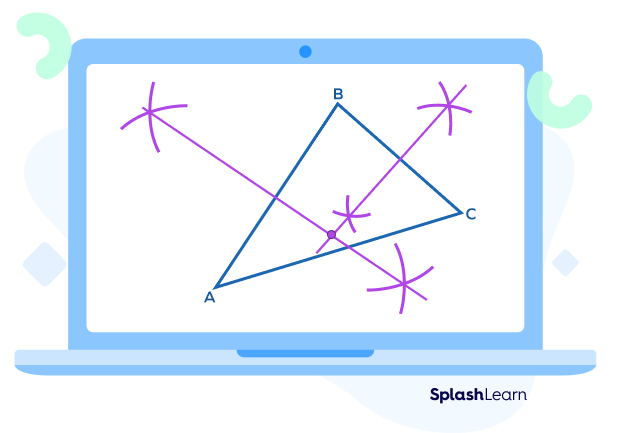
Step 3: Label their point of intersection as O. Using O as the center and keeping OC as distance, draw a circle around the triangle touching all the three vertices or corners of the triangle.
Circumscribed Triangle
A circumscribed triangle is a triangle that is drawn around another geometric shape in such a way that it touches the inside shape at maximum points without ever cutting it. Here, the triangle is the outside shape.
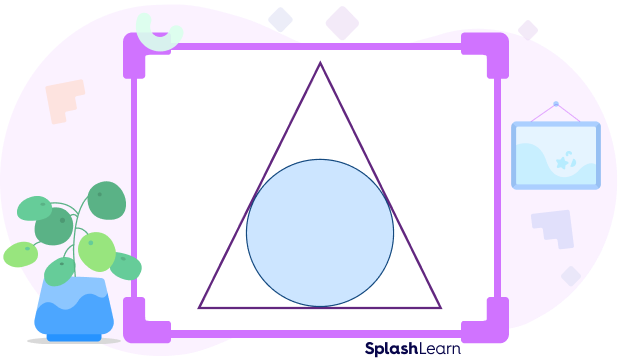
The triangle in the above figure surrounds the circle in such a way that its sides are tangent to the circle. We can also term it as a circle inscribed in a triangle.
Circumscribed Polygon
A circumscribed polygon surrounds a geometric shape in a way that all of its vertices touch the boundaries of the polygon (regular or irregular).
Circumscribed Quadrilateral
A circumscribed quadrilateral encloses a geometric figure in such a way that its sides pass through maximum points of the inside shape without crossing it.
The figure below shows a quadrilateral enclosing a circle. Here, the sides of the quadrilateral act as a tangent to the circle. Note that not all quadrilaterals can be circumscribed.

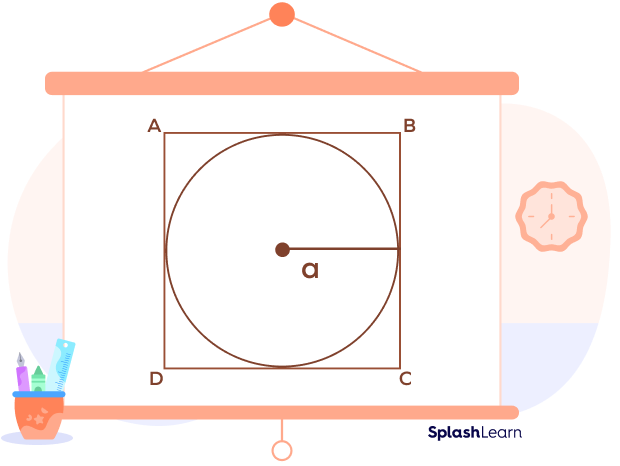
When a square circumscribes a circle, the diameter of the circle equals the side of the square.
Here, the square ABCD circumscribes the circle with radius a such that the side of the square = 2a.
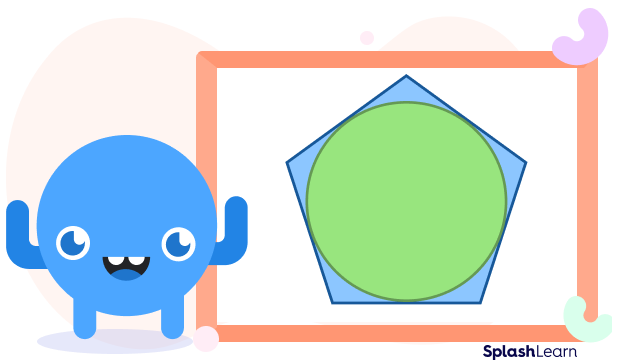
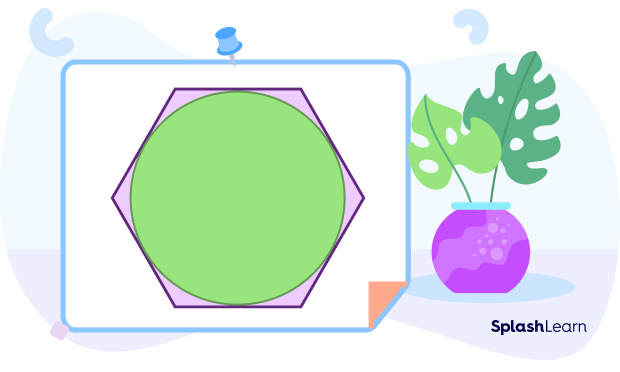
Circumscribed Hexagon
A circumscribed hexagon surrounds a geometric figure so that it passes through each vertex of the inside shape.
In the given figure, a hexagon circumscribes a circle.
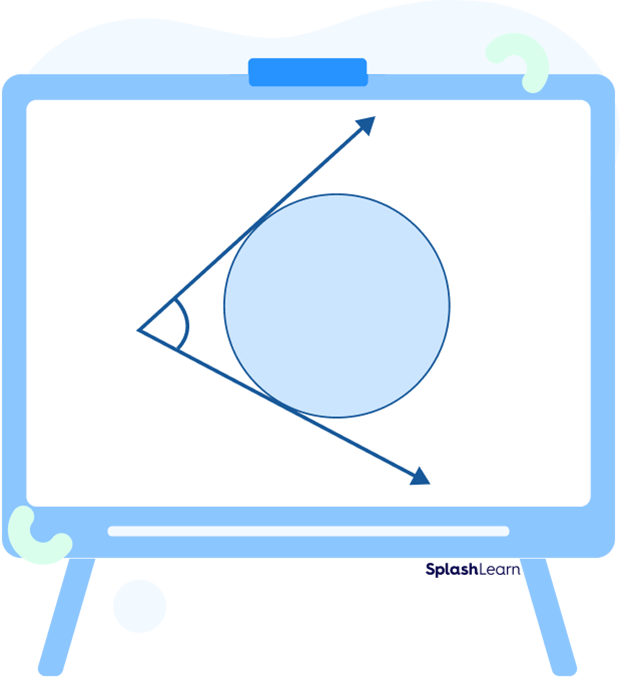
Circumscribed Angle
When the arms of an angle touch the circle forming two tangents, the angle is said to be a circumscribed angle.
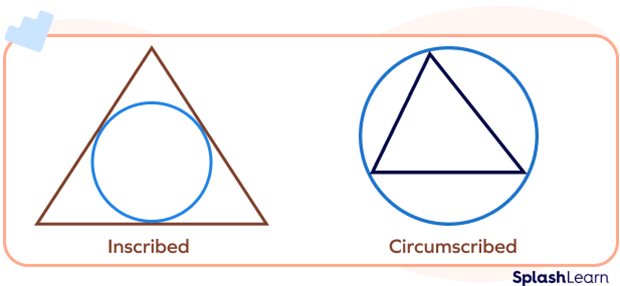
Circumscribed vs. Inscribed
A geometrical shape drawn inside another shape such that all its vertices touch the outer shape without crossing it, the inside shape is called inscribed shape. A circumscribed figure is a shape drawn outside another shape.
We have to first understand which figure we want to describe before using the terms circumscribed and inscribed.
In the left image, we have an inscribed circle of a triangle.
(Note: We can also call this a circumscribed triangle.)
In the right image, we have the circumcircle, the circle circumscribes a triangle.
(Note: We can also call this an inscribed triangle.)
Facts about Circumscribed Shapes
- Circumscribing involves placing one shape around another so that the outer shape touches maximum points of the inside shape.
- They can be found in many geometric figures like triangles and circles.
- The circumscribed circle of a polygon is the smallest circle that contains all its vertices.
Conclusion
In this article, we learned about different circumscribed shapes. Let’s solve a few examples and practice problems for better understanding.
Solved Examples on Circumscribed Shapes
1. A square circumscribes a circle with radius of 10 units. What is the area of the square?
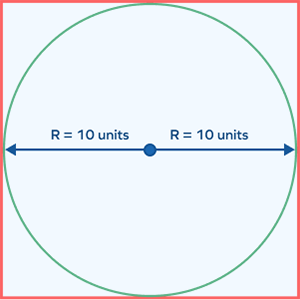
Solution:
The square circumscribes a circle.
Radius of circle = 10 units
Diameter of circle = 20 units
Diameter of circle = Side of square = 20 units
Area of square = side2= 202 = 400 square units
2. The quadrilateral ABCD is encircled by a circle, as indicated in the illustration. Find the missing angles.
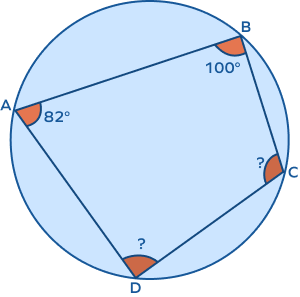
Solution:
The sum of the opposite sides of a quadrilateral enclosed in a circle equals 180 degrees.
Therefore,
∠A + ∠C = 180°
82°+∠C = 180°
∠C = 180° − 82°
∠C =98°
Similarly,
∠B +∠D = 180°
∠100°+∠D = 180°
∠D = 180°−∠100°
∠D = 80°
As a result, C = 102° and D = 75°.
Practice Problems on Circumscribed Shapes
Circumscribe in Math: Definition with Examples
When a circle is drawn outside a figure in a manner that it is passing through all the vertices of the figure but not intersecting it, then it is called _________.
A circumscribed circle is a circle drawn around a geometrical figure.
Which option correctly describes the given diagram?
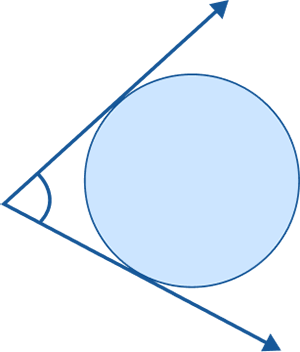
The angle whose arms are tangents to a circle is known as the circumscribed angle.
The given diagram represents a
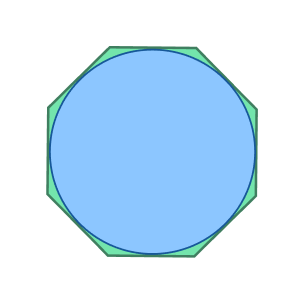
This is a circumscribed polygon (octagon). It circumscribes a circle.
What is the meaning of circumscribed shape?
Circumscribe refers to drawing a shape around another shape such that the outer shape touches the corner points of the inside shape but not crossing it.
The fancy clock shown below represents a

This is a circumscribed triangle. A triangle has a circle inscribed inside. The triangle circumscribes the circular clock. We can also call this as an inscribed circle of a triangle.
Frequently Asked Questions on Circumscribed Shapes
What is an incircle of a triangle?
It is the largest circle drawn within the triangle. It is the circle inscribed in a triangle that touches the three sides.
Do all triangles and quadrilaterals have circumcircles?
All triangles have a circumcircle, but all quadrilaterals do not. A rhombus (which is not a square) cannot have a circumcircle.
What is the meaning of inscribed shape?
It means a shape drawn within another such that maximum points on the boundaries touch but the shapes do not intersect.
What is the circumcenter of a triangle?
The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of the triangle intersect.
















