Constant Polynomial: Definition, Degree, Graph, Examples, FAQs

What Is a Constant Polynomial?

A constant polynomial is a polynomial with only a constant term and no variable. It is a polynomial expression with only a single term, which is a constant. 

We express a constant polynomial as $P(x) = c$, where c is a constant. 

Constant polynomial examples:

• $f(x) = 5$
• $p(x) = 1$
• $g(x) = 0.5$

Note that f(x)=0 is a special case of a constant polynomial and it is called a zero polynomial.

Constant Polynomial Definition

A constant polynomial is a polynomial of the form $P(x) = c$, for all real x, where c is a constant (a real number). 

Degree of a Constant Polynomial

The degree of a constant polynomial is 0. The degree represents the highest power of the variable present in a polynomial.

We can represent the polynomial $P(x) = c$ as $P(x) = c.x0$

Thus, the degree of a constant polynomial is 0 regardless of the constant present.

Note: If $c = 0$, we get a zero polynomial $P(x) = 0$ and the degree of a zero polynomial is not defined.

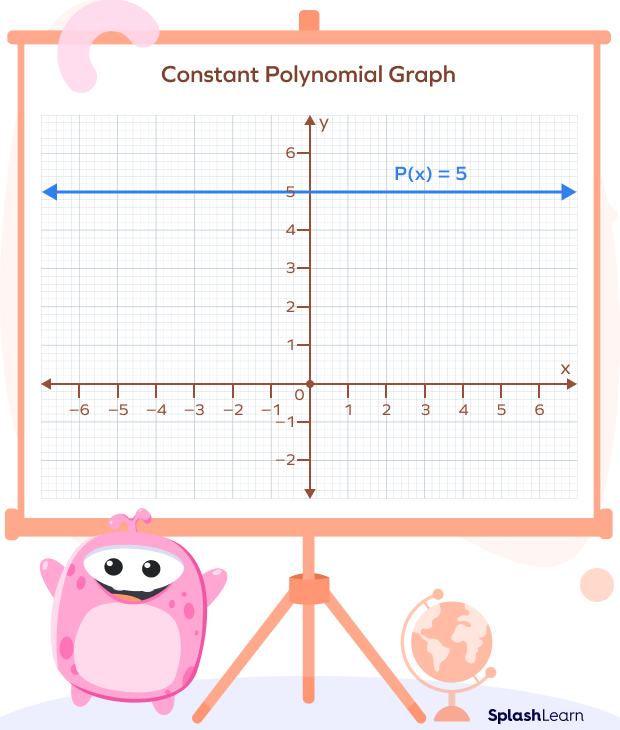
Constant Polynomial Graph

The graph of a constant polynomial is a horizontal line parallel to the x-axis. Since the value of the polynomial remains the same regardless of the variable, the graph remains at a constant height above or below the x-axis, depending on the value of the constant. 

For example, the constant polynomial $P(x) = 5$ graph is a straight line parallel to the x-axis at $y = 5$.

Difference between Constant Polynomial and Zero Polynomial

Constant Polynomial	Zero Polynomial
Degree $= 0$	Degree is not defined.
It is of the form $P(x) = c$, where c is a real number.	It is of the form $P(x) = 0$.
Its graph is a horizontal line parallel to the x-axis.	Its graph is the x-axis.
For a constant polynomial function, Domain $= R$ Range $= \left\{c\right\}$	For a zero polynomial function, $Domain = R$ $Range = \left\{0\right\}$
We get a constant polynomial, when the degree of each term (each monomial) is 0.	We get a zero polynomial, when the coefficients of all variables are 0.

Facts about Constant Polynomials:

Conclusion

In this article, we learned about constant polynomials, their general form, graph, and degree. We also discussed the difference between constant polynomial and zero polynomial. Let’s solve a few examples and MCQs on constant polynomials for revision!

Solved Examples of Constant Polynomials:

1. Find the constant term in the polynomial $P(x) = 3x^{2} + 7x + 9$.

Solution:

To find the constant term, we look for the term without any variable (term where the degree of x is 0). 

In this case, the constant term is 9.

2. Determine the degree of the polynomial P(x) = 4.

Solution:

P(x) = 4

This is a constant polynomial.

We can express the polynomial in terms of x as

P(x) = 4x⁰

So, the degree of the polynomial is 0.

3. Find the value of the polynomial P(x) = 5.9 at x = 10.

Solution:

P(x) = 5.9 is a constant polynomial.

So, for any value of x, the polynomial will give the same value, which is 5.9.

Thus, P(10) = 5.9

4. Find the sum of two constant polynomials: P(x) = 4 and Q(x) =-2.

Solution:

The sum of two constant polynomials is obtained by adding their constant values. It is a constant polynomial again.

In this case, P(x) + Q(x) = 4 + ( – 2) = 2.

Practice Problems on Constant Polynomials

Frequently Asked Questions on Constant Polynomials