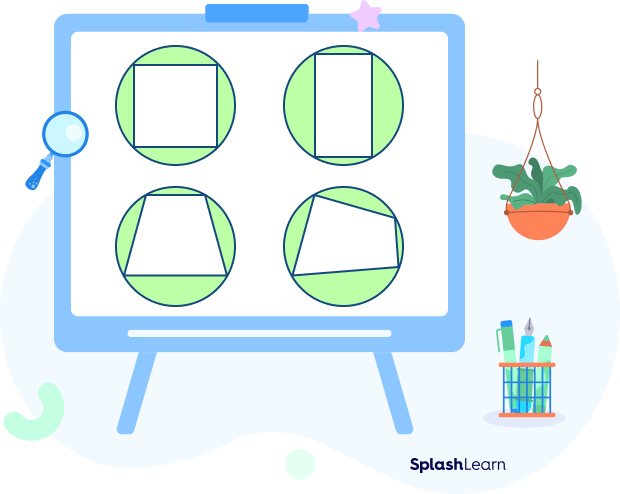
What Is a Cyclic Quadrilateral?
A cyclic quadrilateral is a quadrilateral whose all four vertices lie on a circle. It is also called an inscribed quadrilateral.
The circle that passes through the four vertices of a quadrilateral is called a circumcircle. The vertices of a cyclic quadrilateral are said to be concyclic since they lie on a circle.
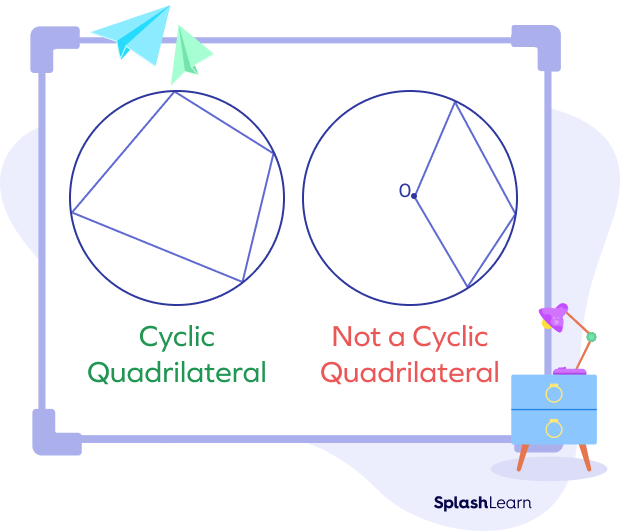
In the image given below, the quadrilateral on the right is not cyclic since its one vertex does not lie on the circumference of the circle.
Recommended Games
Cyclic Quadrilateral Definition
A cyclic quadrilateral can be defined as a quadrilateral inscribed in a circle. It is a four-sided polygon around which a circle can be drawn such that the vertices lie on the circumference of a circle.
Cyclic Quadrilateral Theorems
One important question is: how do you prove that a quadrilateral is cyclic? Let’s understand how to find cyclic quadrilaterals with the help of theorems.
Ptolemy Theorem of Cyclic Quadrilateral
The Ptolemy theorem states that the sum of the product of the opposite sides of a cyclic quadrilateral equals the product of diagonals.
Consider a cyclic quadrilateral ABCD with successive vertices A, B, C, and D, sides given by $a = AB,\; b = BC,\; c = CD,\; d = DA$, and diagonals $p = AC,\; q = BD$.
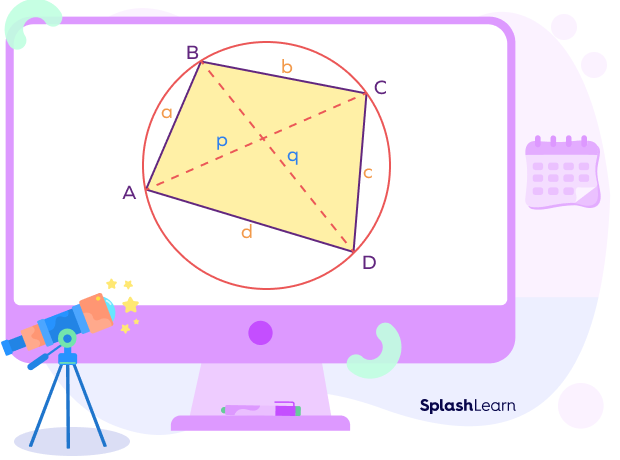
We can express diagonals in terms of the sides as:
$p \times q = (a \times c) + (b \times d)$
$pq = ac + bd$
Cyclic Quadrilateral Angles
To Prove: Opposite Angles of a Cyclic Quadrilateral are Supplementary.
Or
$\angle A +\angle C = 180^{\circ}$ and $\angle B + \angle D = 180^{\circ}$.
Construction: Join the vertices A and C with the center of the circle O.
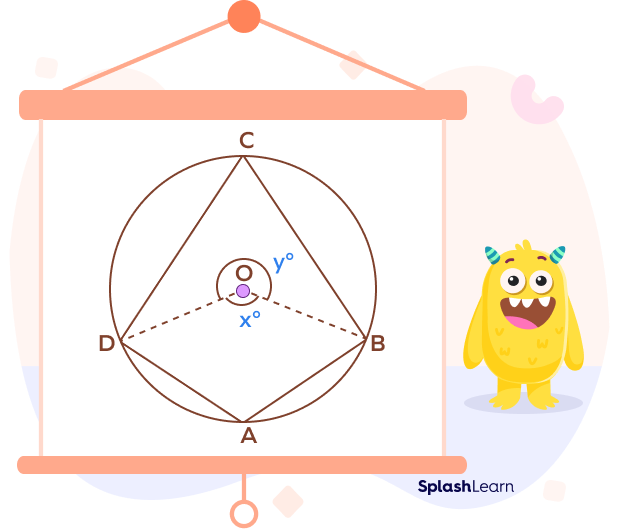
Let x and y be the angles subtended by the minor arc BAD and the major arc BCD respectively.
$x^{\circ} = 2 \angle BCD = 2 \angle C$ …Inscribed angle theorem (angle subtended by the same arc is half the angle subtended at the center)
$y^{\circ} = 2 \angle BAD = 2 \angle A$ …Inscribed angle theorem
Angles $x^{\circ}$ and $y^{\circ}$ together form a full angle.
$x^{\circ} + y^{\circ} = 360^{\circ}$
$2 \angle C + 2 \angle A = 360^{\circ}$
$\angle C + \angle A = 180^{\circ}$
Hence, proved.
The converse of the above theorem is also true.
Converse: If opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Brahmagupta Theorem of Cyclic Quadrilateral
| The Brahmagupta theorem states that the area A of a cyclic quadrilateral whose sides are a, b, c, d is given by: $Area = \sqrt{(s\;-\;a)(s\;-\;b)(s\;-\;c)(s\;-\;d)}$ Here, s is the semi-perimeter given by $s = \frac{a + b + c + d}{2}$ |
Isosceles Trapezoid Theorem
The isosceles trapezoid theorem states that a trapezoid is cyclic quadrilateral if and only if it is an isosceles trapezoid.
An isosceles trapezoid is a trapezoid where the two legs of the trapezoid are equal in length.
Properties of a Cyclic Quadrilateral
- All the four vertices of the inscribed quadrilateral lie on the circumference or boundary of the circle. They are said to be concyclic.
- The four sides of the inscribed quadrilateral are chords of the circle as their endpoints lie on the boundary of the circle.
- The measure of an exterior angle at a vertex equals the opposite interior angle.
- In a cyclic quadrilateral, the sum of the product of the opposite sides equals the product of diagonals.
- In a cyclic quadrilateral, the perpendicular bisectors of the sides are always concurrent and they meet at the center O.
- The sum of a pair of opposite angles is always supplementary.
- The sum of all four angles of a cyclic quadrilateral is $360^{\circ}$.
- A cyclic quadrilateral has the maximum area possible with the given side lengths. In other words, a quadrilateral that is inscribed in a circle represents the maximum area possible with those side lengths.
Cyclic Quadrilateral Formulas
Let’s look at the formulas associated with the cyclic quadrilaterals.
Radius of a Cyclic Quadrilateral
If a, b, c and d are the successive sides of a cyclic quadrilateral, and s is the semi-perimeter, then the radius is given by
$R = \frac{1}{4} \sqrt{\frac{(ab + cd)(ac + bd)(ad + bc)}{(s\;-\;a)(s\;-\;b)(s\;-\;c)(s\;-\;d)}}$
Diagonals of a Cyclic Quadrilateral
Suppose a, b, c, and d are the sides of a cyclic quadrilateral and p & q are the diagonals, then the formula for the length of diagonals is given by:
$p = \sqrt{\frac{(ac+bd)(ad+bc)}{ab+cd}}$ and $q = \sqrt{\frac{(ac + bd)(ab + cd)}{ad + bc}}$
Area of a Cyclic Quadrilateral
As mentioned earlier, if the sides of the inscribed quadrilateral are a, b, c, and d and “s” is the semiperimeter, then the area of a cyclic quadrilateral is given by the Brahmagupta theorem:
$Area = \sqrt{(s\;-\;a)(s\;-\;b)(s\;-\;c)(s\;-\;d)}$
where $s = \frac{a + b + c + d}{2}$
Heron’s formula for the area of a triangle is derived from this equation.
Facts about Cyclic Quadrilateral
- A cyclic quadrilateral has the maximum area possible with the given side lengths.
- The circle that has all the vertices of a polygon on its circumference is called the circumcircle or circumscribed circle.
Conclusion
In this article, we learned about cyclic quadrilaterals, their properties, important theorems, and formulas associated with them. Now, let’s understand how to solve cyclic quadrilateral problems with the help of these properties and theorems.
Solved Examples on Cyclic Quadrilateral
1. Find the values of x and y.
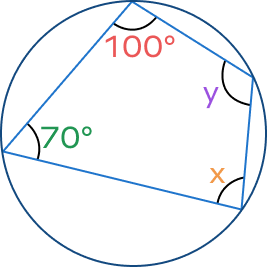
Solution:
We know that opposite angles of a cyclic quadrilateral are supplementary.
So, $100^{\circ} + x = 180^{\circ}$
$x = 180^{\circ}\;-\;100^{\circ}$
$x = 80^{\circ}$
Similarly, $70^{\circ} + y = 180^{\circ}$
$y = 180^{\circ} \;-\; 70^{\circ}$
$y = 110^{\circ}$
2. Find the value of x and y in the following figure.
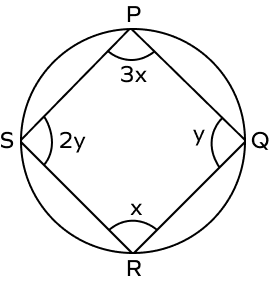
Solution:
We know that opposite angles of a cyclic quadrilateral are supplementary.
So, $\angle P + \angle R = 180^{\circ}$ and $\angle S + \angle Q = 180^{\circ}$
$3x + x = 180^{\circ}$ and $2y + y = 180^{\circ}$
$4x = 180^{\circ}$ and $3y = 180^{\circ}$
$\Rightarrow x = \frac{180^{\circ}}{4} = 45^{\circ}$ and $y = \frac{180^{\circ}}{3} = 60^{\circ}$
So, $x = 45^{\circ}$ and $y = 60^{\circ}$
3. Find the value of $\angle RQS$ in the following figure.
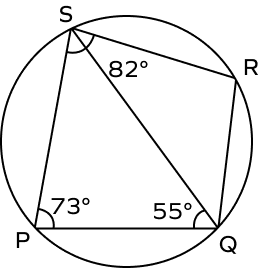
Solution:
We know that opposite angles of a cyclic quadrilateral are supplementary.
So, $\angle PSR + \angle RQP = 180^{\circ}$
$82^{\circ} + \angle RQP = 180^{\circ}$
$\angle RQP = 180^{\circ} \;–\; 82^{\circ} = 98^{\circ}$
Now,
$\angle PQS + \angle RQS = \angle RQP$
$55^{\circ} + \angle RQS = 98^{\circ}$
$\angle RQS = 98^{\circ} \;–\; 55^{\circ}$
$\angle RQS = 43^{\circ}$
4. Find the value of $\angle BCD$ in the following diagram.
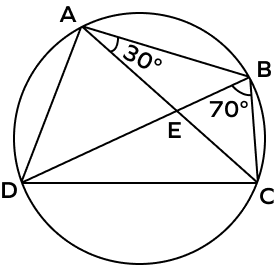
Solution:
$\angle DAC = \angle DBC$ (Angles in the same segment are equal)
Thus, $\angle DAC = 70^{\circ}$
$\angle DAB = \angle DAC + \angle BAC$
$\angle DAB = 70^{\circ} + 30^{\circ} = 100^{\circ}$
We know that opposite angles of a cyclic quadrilateral are supplementary.
$\angle DAB + \angle DCB = 180^{\circ}$
$100^{\circ} + \angle DCB = 180^{\circ}$
$\angle DCB = 180^{\circ}\; – \;100^{\circ}$
$\angle DCB = 80^{\circ}$
5. Find the area of a cyclic quadrilateral whose sides are 2 inches, 4 inches, 10 inches, and 12 inches.
Solution:
Let ABCD be the cyclic quadrilateral.
$a = 2,\; b = 4,\; c = 10,\; d = 12$
Semi-perimeter $= s = \frac{a + b + c + d}{2} = \frac{2 + 4 + 10 + 12}{2} = \frac{28}{2} = 14$
$Area = \sqrt{(s\;-\;a)(s\;-\;b)(s\;-\;c)(s\;-\;d)}$
$= \sqrt{(14\;-\;2)(14\;-\;4)(14\;-\;10)(14\;-\;12)}$
$= \sqrt{12\times10\times4\times2}$
$= \sqrt{2\times2\times3\times2\times5\times2\times2\times2}$
$= 8\sqrt{15}$ square inches
Practice Problems on Cyclic Quadrilateral
Cyclic Quadrilateral – Definition, Theorem, Examples, FAQs
Find the value of x in the following figure.
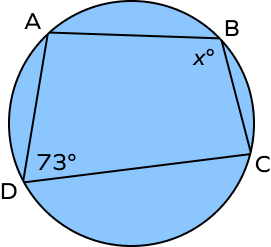
We know that opposite angles of a cyclic quadrilateral are supplementary.
So, $\angle ABC + \angle ADC = 180^{\circ}$
$x + 73^{\circ} = 180^{\circ}$
$\angle DCB = 180^{\circ} \;–\; 73^{\circ} = 107^{\circ}$
What is the value of $\angle BCD$ in the following figure?
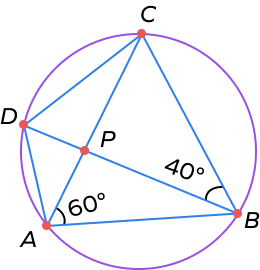
$\angle CBD = \angle CAD$ (Angles in the same segment are equal)
$\angle CAD = 40^{\circ}$
$\angle BAD = \angle BAC + \angle CAD$
$\angle BAD = 60^{\circ} + 40^{\circ} = 100^{\circ}$
We know that opposite angles of a cyclic quadrilateral are supplementary.
$\angle BAD + \angle BCD = 180^{\circ}$
$100^{\circ} + \angle BCD = 180^{\circ}$
$\angle BCD = 180^{\circ}\;–\;100^{\circ} = 80^{\circ}$
$\angle BCD = 180^{\circ}\;–\;110^{\circ} = 70^{\circ}$
What is the value of x in the following figure?
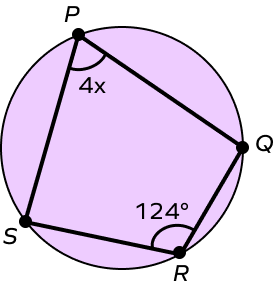
We know that opposite angles of a cyclic quadrilateral are supplementary.
$\angle SPQ + \angle SRQ = 180^{\circ}$
$4x + 124^{\circ} = 180^{\circ}$
$4x = 180^{\circ} \;–\; 124^{\circ}$
$4x = 56^{\circ}$
$x = 16^{\circ}$
Frequently Asked Questions on Cyclic Quadrilateral
Is every quadrilateral cyclic?
No. Not every quadrilateral is cyclic. Examples of non-cyclic quadrilaterals are non-square rhombus (rhombus that’s not a square) and non-rectangular parallelogram.
Is a parallelogram a cyclic quadrilateral?
If a parallelogram is cyclic, it must be a rectangle. A cyclic parallelogram is always a rectangle. A non-rectangular parallelogram is not cyclic.
Do angles in a cyclic quadrilateral add up to $360^{\circ}$?
Yes, angles in a cyclic quadrilateral add up to $360^{\circ}$ as the sum of opposite angles is $180^{\circ}$. So, $180^{\circ} + 180^{\circ} = 360^{\circ}$.
Is a rhombus a cyclic quadrilateral?
A non-square rhombus is not cyclic. A rhombus cannot be a cyclic quadrilateral because the opposite angles of a cyclic quadrilateral are supplementary, but in the case of a rhombus, the opposite angles are equal. A cyclic rhombus is a square.





















