Convert Decimal To Binary – Formula, Table, Facts, Examples, FAQs

What Is Decimal to Binary Conversion?

In the decimal to binary conversion, we convert a given base-10 number into an equivalent base-2 number. 

For example, the binary equivalent of 5 is (101)₂. 

Writing any decimal number in binary simply means finding a number equivalent to it in the binary number system.

Note that there is no decimal to binary formula for direct conversion. Decimal to binary conversion is a process done by dividing the decimal number to 2. Note down all the remainders. Continuous division is carried out until the quotient reaches 0. Writing all the remainders in reverse order we get the equivalent binary number. 

Example: 21₁₀ = 10101₂

What Is Decimal Number System?

The decimal number system, also known as the Hindu-Arabic number system, is the base-10 number system. It uses the 10 digits or symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

It is the most commonly used number system. Thus, if the base is not mentioned, the number is considered to be a decimal number. 

Each digit in the decimal system has a place value depending upon its position and the place value of every digit is ten times more significant than the previous digit. In the decimal system there are place values as ones, tens, hundreds, thousands, etc. (increasing power of 10).

Example 1: 42 is a decimal number, then place value of 2 is one, and its value is 2 × 1 = 2 and place value of 4 is ten  and its value is  4 × 10 = 40 . 

 Let us look some more example for a better understanding, 

Example 2: 15 = (15)₁₀ = 1 × 10 + 5  × 1 

Example 3: 245 = (245)₁₀ = 2 × 10² + 4 × 10 + 5 × 1

Example 4: 2000 = (2000)₁₀ = 2 × 10³ + 0 × 10² + 0 × 10 + 0 × 1

Example 5: 35.55 = (35.55)₁₀ = 3 × 10² + 5 × 10¹ + 5 × 10^-1+ 5 × 10^-2

What Is Binary Number System?

The binary number system is a base-2 number system in which numbers are represented using only two digits: 0 and 1.

Each digit of the binary number system is called a bit. Bit can either be 0 or 1.

Example: 1101 is a four-bit binary number. 

      100001 is a six-bit binary number.

The Most Significant Bit (MSB) is the bit on the far left end of a binary number, while the Least Significant Bit (LSB) is the bit on the far right end (LSB).

In the binary system, the place values go like ones, twos, fours, etc (increasing power of 2).

How to Convert Decimal Numbers into Binary Numbers

To convert decimal numbers to binary, we divide the given decimal number repeatedly by 2 and the remainder are noted down till we get 0 as the final quotient. 

Here are the steps for converting decimal numbers into binary:

Step 1: Divide the given decimal number by 2 and note down the remainder and quotient.

Step 2: Now, divide the quotient obtained in step 1 by 2, and note down the remainder again.

Step 3: Repeat the above steps until you get 0 as the quotient.

Step 4: Now, write the remainders in the reverse order (from the last to the first).

The Least Significant Bit (LSB) of the binary number is at the top and the Most Significant Bit (MSB) is at the bottom.

Example: Convert 14₁₀ into binary.

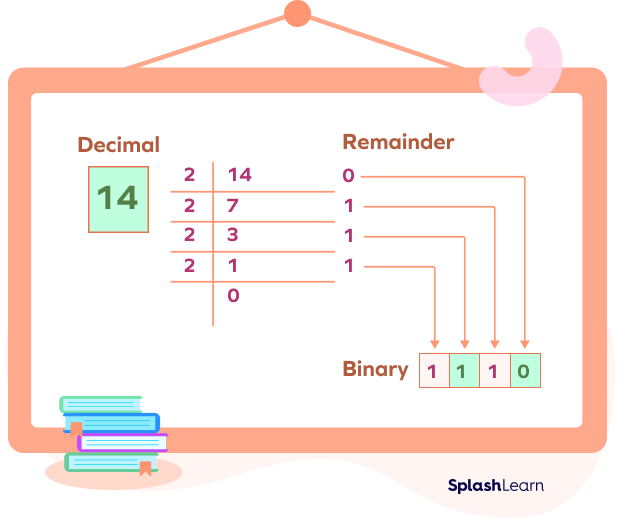
How to Convert Decimal Fraction into Binary

To find the binary equivalent of the decimal fraction, we find the binary equivalent of the integral part and the fractional part separately and add them together to find the answer.

To convert the fractional part into binary, multiply the fractional part of the decimal number repeatedly by 2 and note down the integral part and fractional part of the result. Repeat this process until the fractional part becomes 0.

The answer will be the integral parts obtained in each multiplication (in the right sequence).

Note that if the fractional part is not becoming 0 and if the process goes on, the fractional number will have an infinite length. In such cases, we stop the process when we get the required number of bits.

Example 1: Find the binary fraction equivalent of 0.125₁₀

0.125 × 2 = 0 + 0.250 

0.250 × 2 = 0 + 0.500  

0.500 × 2 = 1 + 0.000  

Thus the binary equivalent of 0.125₁₀ is 0.001.

Example 2: 0.6875₁₀ = 1011₂

0.6875 × 2 = 1 + 0.375

0.3750 × 2 = 0 + 0.75

    0.75 × 2 = 1 + 0.5

    0.50 × 2 = 1 + 0

Decimal to Binary Conversion Table

Decimal Number	Binary Number
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
0.1	0.00011
0.2	0.00110
0.3	0.01001
0.5	0.1
0.6	0.10011
0.7	0.10110
0.8	0.11001
0.9	0.11100

Conclusion

In this article, we learned about decimal to binary conversion along with the steps for the conversion. We also learned how to convert decimal fractions into binary. Let’s solve a few examples based on the decimal to binary conversion.

Facts about Decimal to Binary Conversion

Solved Examples on Decimal to Binary Conversion

Example 1: Convert decimal to binary: 100₁₀

Solution: 

Let Q represent the Quotient and R represent the Remainder.

100 ÷ 2 gives Q = 50 and R = 0

50 ÷ 2 gives Q = 25 and R = 0

25 ÷ 2 gives Q = 12 and R = 1

12 ÷ 2 gives Q = 6 and R = 0

6 ÷ 2 gives Q = 3 and R = 0

3 ÷ 2 gives Q = 1 and R = 1

1 ÷ 2 gives Q = 0 and R = 1

Write down the remainders from last to the first to find the binary conversion of the given decimal number.

100₁₀ = 1100100₂

Example 2: Convert the Decimal Number 144 into a Binary Number.

Solution: 

Division by 2	Quotient	Remainder
144 ÷ 2	72	0
72 ÷ 2	36	0
36 ÷ 2	18	0
18 ÷ 2	9	0
9 ÷ 2	4	1
4 ÷ 2	2	0
2 ÷ 2	1	0
1 ÷ 2	0	1

Hence, 144₁₀ = 10010000₂

Example 3: Convert 13₁₀ to base 2 number system.

Solution: 

Division by 2	Quotient	Remainder
13 ÷ 2	6	1
6 ÷ 2	3	0
3 ÷ 2	1	1
1 ÷ 2	0	1

Hence, 131₁₀ = 1101₂

Example 4: Convert 174.25₁₀ to base 2 number system.

Solution: 

Here, we have to convert decimal fraction to binary.

First, we will find the binary equivalent of 174.

Division by 2	Quotient	Remainder
174 ÷ 2	87	0
87 ÷ 2	43	1
43 ÷ 2	21	1
21 ÷ 2	10	1
10 ÷ 2	5	0
5 ÷ 2	2	1
2 ÷ 2	1	0
1 ÷ 2	0	1

So, the binary equivalent of 174 is 10101110₂.

Next, we find the binary equivalent of 0.25₁₀.

Multiply by 2	Result
0.25 × 2	0 + 0.50
0.5  × 2	1 + 0

Thus, the binary equivalent of  0.25₁₀ is 0.01

The binary equivalent of 174.25₁₀ is 10101110 + .0.01 = 10101110.01

Example 5: Convert 10.2₁₀ to base 2 number system.

Solution:  

First we will find the binary equivalent of the integral part of the number that is 10.

10 ÷ 2	5	0
5 ÷ 2	2	1
2 ÷ 2	1	0
1 ÷ 2	0	1

Thus, 10₁₀ = 1010₂

Now, let’s find the binary equivalent of 0.2.

0.2 × 2 = 0 + 0.4 

0.4 × 2 = 0 + 0.8 

0.8 × 2 = 1 + 0.6 

0.6 × 2 = 1 + 0.2 

Write the integer values obtained in each multiplication to find the answer.

Thus 0.2₁₀ = 0.0011₂

In conclusion, the binary equivalent of 10.2 is the sum of 10102₂ and 0.0011₂.

10.2₁₀ =  1010₂ +  0.0011₂ = 1010.0011₂.

Practice Problems on Decimal to Binary Conversion

Frequently Asked Questions about Decimal to Binary Conversion