What Is the Formula for Diameter?
To determine the length of the diameter of a circle, we use the diameter formula. The diameter of a circle is twice the length of its radius.
Diameter $= 2 \times$ Radius
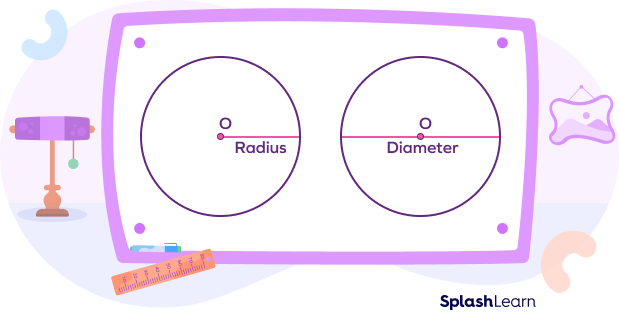
What is the diameter of a circle?
A diameter is a line segment that passes through the center of a circle connecting distinct points on the boundary of the circle. A circle has infinite diameters since there are an infinite number of points on the circumference of a circle.
Recommended Games
Diameter of a Circle: Formulas
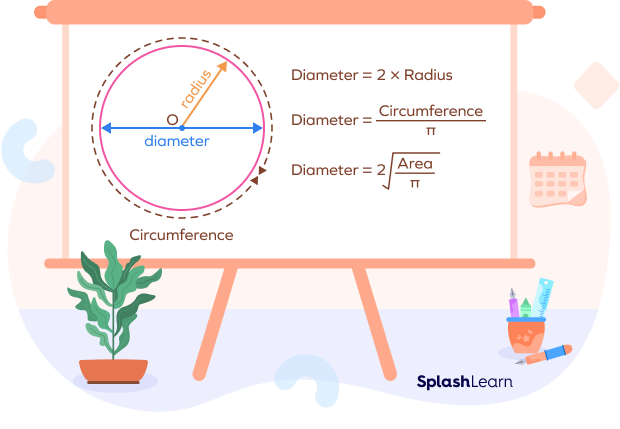
We can write the formula for diameter in different ways since we can express it in terms of radius, circumference, and area.
| Description | Formula |
|---|---|
| Diameter Formula in terms of radius | Diameter $= 2 \times $Radius |
| Diameter Formula in terms of circumference | Diameter $= \frac{Circumference}{\pi}$ |
| Diameter Formula in terms of area | Diameter $= 2\sqrt{\frac{Area}{\pi}}$ |
How to Calculate Diameter
We must have information about the radius or the other above-mentioned measurements to calculate the diameter of the circle. We can calculate the diameter using the circle’s distinct diameter formula. They are as follows.
Finding diameter using circumference
Circumference of a circle $= 2\pi r$
Since $2r =$ diameter $= d$, we write the above formula as:
Circumference of a circle $= \pi d$
Thus, by rearranging the formula, we get the circle diameter formula using circumference,
Diameter $= \frac{Circumference}{\pi}$
Example: If the circumference of a circle is 72 units, find the diameter.
$C = 72$ units
Diameter $= d = \frac{72}{\pi}$
$d = \frac{72}{3.14}$
$d = 22.92$ units
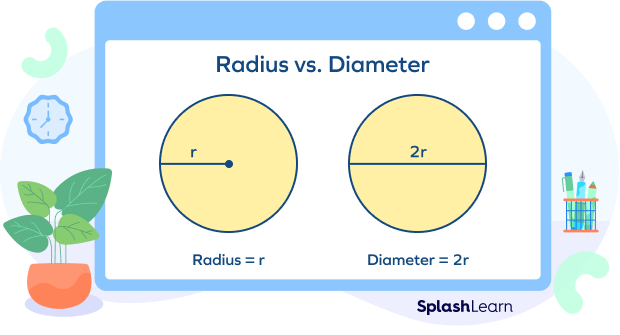
Finding diameter using radius of a circle
Let’s understand how to find diameter with radius.
The radius is the distance from the center of a circle to the boundary.
Therefore, the diameter formula using radius is given as
Diameter $= 2 \times$ Radius of the circle
Example: A circle has a radius of 14 units. Find its diameter.
Diameter $= 2\times$ Radius $= 2 \times 14 = 28$ units
Finding diameter using area of circle
Area of a circle is the total 2D region covered by the circle.
Area of a circle $= \pi r^{2}$
$r^{2} = \frac{Area}{\pi}$
Radius $= \sqrt{\frac{Area}{\pi}}$
Diameter $= 2 \times$ Radius
Diameter $= 2 \times \sqrt{\frac{Area}{\pi}}$
Facts about Diameter Formula
- Diameter is the longest chord of a circle.
- Not every chord is a diameter of the circle, but every diameter of the circle is a chord.
- A chord is the line segment that joins the two points on the circle’s circumference.
- Any tangent line identified to a circle at its point of contact must be perpendicular to its diameter. Thus, the tangent line and the circle’s diameter form a 90 degree angle between them.
Conclusion
In this article, we learned different formulas to find the diameter of a circle. We can express the diameter of a circle in terms of radius, area, and also the circumference. Let’s solve a few examples and practice MCQs based on the diameter formulas.
Solved Examples of Diameter Formula
1. The radius of a circle is given as 25 units. Find the diameter of the circle.
Solution:
Radius $= 25$ units
Diameter formula using radius:
Diameter $= 2\times$ Radius
Diameter $= 2 \times 25$
Diameter $= 50$ units
Therefore, the diameter of the circle with the radius of 25 units is 50 units.
2. If the circumference of a circle is 5 units. Find the diameter of the circle.
Solution:
Circumference of the circle $= 5\pi$ units
Using the diameter formula with circumference, we get
Diameter $= \frac{Circumference}{\pi}$
Diameter $= \frac{5}{\pi}$
Diameter $= 5$ units
3. Find the radius of the circle using the diameter formula when the diameter given is 14 inches.
Solution:
Diameter $= 14$ inches
Diameter $= 2 \times$ Radius
By altering the formula, we get
Radius $= \frac{Diameter}{2}$
Radius $= \frac{14}{2}$
Radius $= 7$ inches
4. Find the diameter of the circle with area 72 unit2.
Solution:
Area $= 72\; unit^{2}$
$\pi r^{2} = 72$
$r^{2} = \frac{72}{3.14}$
$r ≈ 4.78$ units
Thus, diameter $= 2r ≈ 9.57$ units
Practice Problems on Diameter Formula
Diameter Formula: Definition, Facts, Examples, Practice Problems
The diameter formula using the area of the circle is
The formula to find the diameter of the circle using area is expressed as
Radius $=2\sqrt{\frac{Area}{\pi}}$
The formula for the circumference of the circle is
The circumference of the circle can be calculated using the formula Circumference $= \pi \times Diameter$.
Diameter is the longest ________ of a circle.
Diameter is the longest chord of a circle.
Diameter of a unit circle is
Radius of a unit circle = 1 unit
Diameter of a unit circle = 2 units
Radius is
Radius is defined as half of the length of the circle’s diameter.
Frequently Asked Questions about Diameter Formula
Can the diameter be negative or zero?
No, the diameter of the circle can neither be negative nor zero. It always is a positive value since it represents the length of a line segment.
Is the circumference of a circle directly proportional to the diameter?
Yes, the circumference of a circle is directly proportional to the diameter. If the diameter increases, the circumference increases. If the diameter increases, the circumference decreases.
How many radii can be formed in a circle?
Each circle possesses an uncountable number of the radius that possesses the same length in a circle.
What is the diameter to radius formula?
Radius = Diameter $\div$ 2

















