Dividing Mixed Numbers

Dividing Mixed Numbers – Introduction

Imagine a situation where you have to divide $3\frac{1}{2}$ muffins equally among 2 friends. How would you divide a number like $3\frac{1}{2}$ ? Here, $3\frac{1}{2}$ is a “mixed number” since it contains a fraction $\frac{1}{2}$ and also a whole number 3.

What Are Mixed Numbers?

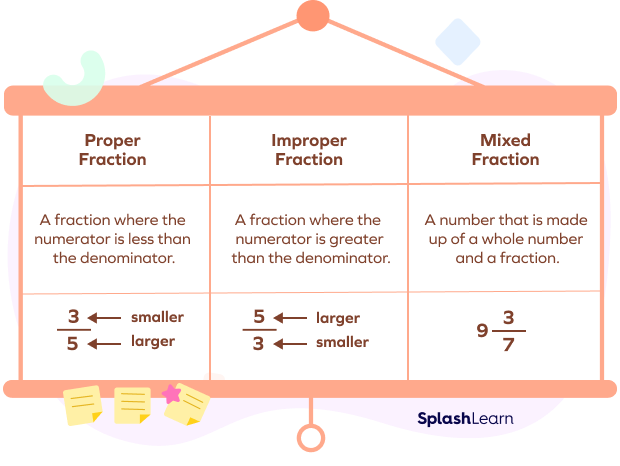
A fraction can be divided into three categories based on the value of numerator and denominator.

• Proper fractions
• Improper fractions
• Mixed fractions or mixed numbers

Proper Fractions

Proper fractions are fractions where the numerator is less than the denominator. 

Example: $\frac{2}{5}, \frac{3}{7}$, etc. 

Improper Fractions

Improper fractions are fractions where the numerator is equal to or greater than the denominator. Example: $\frac{5}{4}, \frac{7}{5}$, etc. 

Mixed Numbers

A mixed number is a whole number and a proper fraction represented together. Mixed numbers and improper fractions basically represent the same thing but we write them into different formats. It generally represents a number between any two whole numbers. For example, $3\frac{1}{2}$ lies between 3 and 4; $2\frac{3}{5}$ lies between 2 and 3, etc.

(Note that the unwritten sign between the whole number part and the fractional part is for addition, not multiplication!  $1\frac{1}{2}$ a glass of milk means one glass and a half glass!)

Proper fractions always lie between 0 and 1. Improper fractions are greater than 1. Thus, mixed numbers are also always greater than 1. 

Dividing mixed numbers becomes way easier when we convert the mixed numbers into improper fractions. Let’s understand how to convert mixed fractions into improper fractions.

How to Convert Mixed Numbers into Improper Fractions?

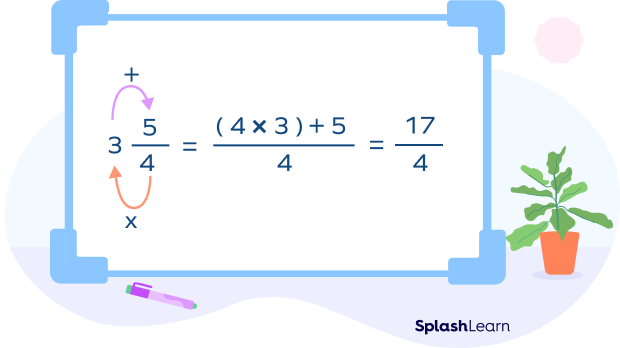
All mixed numbers can be converted to improper fractions and vice versa. To do that, we multiply the denominator by the whole number and add the numerator to this product, as shown in the image below. Converting mixed numbers into improper fractions helps in dividing mixed numbers by fractions or by another mixed number.

Rule to convert a mixed number into an improper fraction is shown below. Note that the denominator stays the same.

Let’s convert a mixed number into an improper fraction.

Examples:

$3\frac{1}{2}  =  \frac{{(3 ×2) + 1}}{2} = \frac{6 + 1}{2} = \frac{7}{2}$

$2\frac{3}{5}  =  \frac{{(2 × 5) + 3}}{5} = \frac{10 + 3}{5} = \frac{13}{5}$

How to Divide Fractions?

A fraction is a part of a whole.

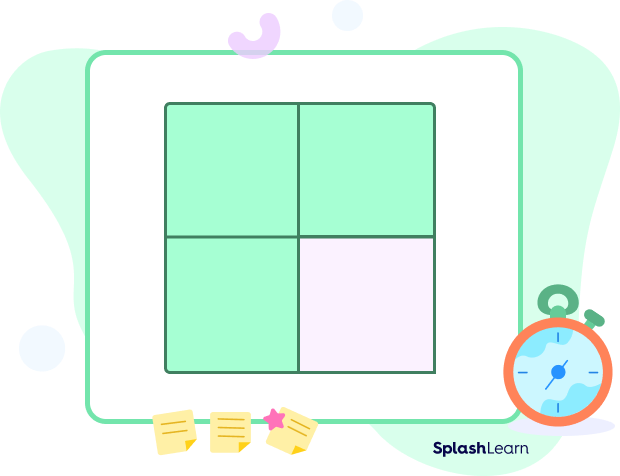
The square is divided equally into 4 parts with 3 parts shaded. That is, 3 out of 4 shaded parts are shaded. So, the fraction is $\frac{3}{4}$. 

The division of  $\frac{3}{4}$ by 6 can be shown as:

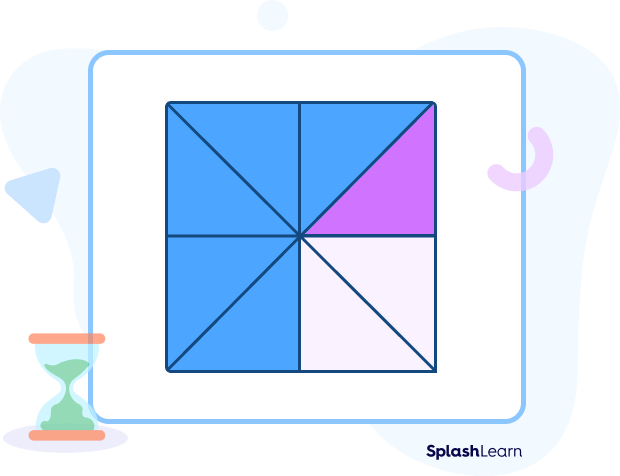
The portion shaded in pink is one-sixth of the fraction $\frac{3}{4}$.

That is,  $\frac{3}{4} \times \frac{1}{6} = \frac{3}{24}  = \frac{1}{8}$

Thus, it is one-eighth of the whole square.

Consider another example where the divisor is a fraction, say   $\frac{3}{4} \div \frac{1}{4}$ 

It is clear that there are 3 one-fourths in a three-fourth.

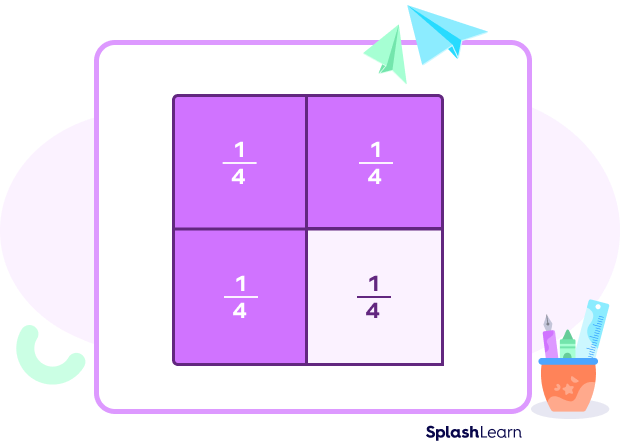
To divide a fraction by another, we multiply the dividend by the reciprocal of the divisor.

So, $\frac{3}{4} \div \frac{1}{4} = \frac{3}{4} \times 4 = 3$

How to Divide Mixed Numbers?

Now that you know how to convert mixed numbers into improper fractions and the concept of reciprocal, the method of dividing mixed numbers or dividing mixed fractions is simple. A mixed number can be divided by another mixed number, fraction, or whole number. Here are  the Dividing Mixed Numbers Examples and the steps for each of the division types. 

1. Dividing a Mixed Number by Another Mixed Number 

First, convert both mixed numbers to improper fractions. Then, take the reciprocal of the second fraction and multiply it with the first fraction. Finally, simplify the answer you get and convert it into a mixed number if required.

For example, let’s solve: 

1) $3\frac{2}{3} \div 2\frac{1}{4}$

$= \frac{11}{3} \div \frac{9}{4}$                         (Convert mixed numbers to improper fractions.)

$= \frac{11}{3} \times \frac{4}{9}$                          (Multiply the dividend by the reciprocal of the divisor.)

$= \frac{44}{27}$

$= 1\frac{17}{27}$                                (Convert the improper fraction into a mixed number.)

2) $3\frac{2}{5} \div 2\frac{1}{5}$

$= \frac{17}{5} \div \frac{11}{5}$                             (Convert mixed numbers to improper fractions.)

$= \frac{17}{5} \times \frac{5}{11}$                             (Multiply the dividend by the reciprocal of the divisor.)

$= \frac{17}{11}$

$= 1\frac{6}{11}$                                       (Convert the improper fraction to a mixed number.)

2. Dividing Mixed Numbers by Fractions 

Convert the mixed number into an improper fraction. Multiply the first fraction with the reciprocal of the second. Finally, simplify the answer you get and convert it into a mixed number if required.

For example, let’s divide the mixed number 2 2/5 by the fraction 3/7.

$2\frac{2}{5} \div \frac{3}{7}$

$= \frac{12}{5} \div \frac{3}{7}$                       (Convert the mixed number to improper fraction.)

$= \frac{12}{5} \times \frac{7}{3}$                       (Multiply the dividend by the reciprocal of the divisor.)

$= \frac{84}{15}$

$= 2\frac{8}{5}$ 

$= 5\frac{3}{5}$                                (Convert the improper fraction to a mixed number.)

3. Dividing Mixed Numbers by Whole Numbers 

Convert the whole number into an improper fraction by taking 1 as the denominator. Then follow the same steps mentioned above for dividing mixed numbers by fractions. 

For instance, in the example mentioned at the beginning of the article, we needed to divide 3 1/2 muffins among 2 friends. Let’s solve that problem.

$3\frac{1}{2} \div 2$

$= \frac{7}{2} \div \frac{2}{1}$                            (Convert the mixed number to improper fraction.)

$= \frac{7}{2} \times \frac{1}{2}$                            (Multiply the dividend by the reciprocal of the divisor.)

$=\frac{7}{4}$

$= 1\frac{3}{4}$                                 (Convert the improper fraction to a mixed number.)

So, each person will receive $1\frac{3}{4}$ of the remaining muffin.

How to Divide Fractions with Mixed Numbers?

Let’s understand how to divide fractions with mixed numbers using an example.

Example: Divide $\frac{3}{7}$ by $2\frac{1}{4}$.

214 as an improper fraction $= \frac{{(2 × 4) + 1}}{4} = \frac{8 + 1}{4} = \frac{9}{4}$

$\frac{3}{7} 2\frac{1}{4}= \frac{3}{7} \div \frac{9}{4} = \frac{3}{7}\times\frac{4}{9}=\frac{12}{63}= \frac{4}{21}$

Solved Examples

1. Find the length of each part if a $3\frac{1}{5}$ feet long wooden stick is divided equally into 7 parts.

Solution: Dividing the mixed number $3\frac{1}{5}$ by 7 will give us the length of each small part.

 $3\frac{1}{5} \div 7$

$= (\frac{16}{5}) \div (\frac{7}{1})$

$= (\frac{16}{5}) \times (\frac{1}{7})$

$= \frac{16}{35}$

Length of each small part $= \frac{16}{35}$ feet

2. Divide $2\frac{2}{3}$ by $\frac{2}{5}$.

Solution:

$2\frac{2}{3} \div \frac{2}{5}$

$= (\frac{8}{3}) \div (\frac{2}{5})$

$= (\frac{8}{3}) \times (\frac{5}{2})$                        (Multiply the dividend by the reciprocal of the divisor.)

$= \frac{40}{6}$

$= \frac{20}{3}$

$= 6\frac{2}{3}$                                   (Convert the improper fraction to a mixed number.)

3. Divide $2\frac{1}{3}$ by $2\frac{4}{5}$.

Solution:

$2\frac{1}{3} \div 2\frac{4}{5}$

$= (\frac{7}{3}) \div (\frac{14}{5})$

$= (\frac{7}{3}) \times (\frac{5}{14})$

$= \frac{35}{42}$

$= \frac{5}{6}$

Practice Problems

Frequently Asked Questions